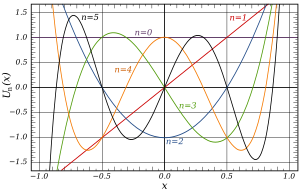
Polinomios de Chebyshev

Los polinomios de Chebyshev son dos secuencias de polinomios relacionados con las funciones coseno y seno , anotados como y . Se pueden definir de varias maneras equivalentes; en este artículo los polinomios se definen comenzando con funciones trigonométricas : $T_{n}(x)$ ${\ estilo de visualización U_ {n} (x)}$

Estas definiciones no parecen ser polinomios, pero al usar varias identidades trigonométricas se pueden convertir a una forma explícitamente polinomial. Por ejemplo, para $n = 2$ , la fórmula $T 2$ se puede convertir en un polinomio con argumento $x = cos(θ)$ , usando la fórmula de doble ángulo :

Los otros $T$ $n$ $($ $x$ $)$ se definen de manera similar, donde para los polinomios del segundo tipo ( $U$ $n$ ) debemos usar la fórmula de De Moivre para obtener $sin($ $nθ$ $)$ como $sin($ $θ$ $)$ por un polinomio en $cos($ $θ$ $)$ . Por ejemplo,

Una vez convertidos a la forma polinomial, $T n (x)$ y $U n (x)$ se denominan polinomios de Chebyshev de primera y segunda clase respectivamente.

Por el contrario, una potencia entera arbitraria de funciones trigonométricas puede expresarse como una combinación lineal de funciones trigonométricas usando polinomios de Chebyshev

donde el número primo en el símbolo de suma indica que la contribución de $j = 0$ debe reducirse a la mitad si aparece, y . $T_{j}(\cos \theta)=\cos(j\theta)$

Gráfico de los primeros cinco polinomios

T n

Chebyshev del primer tipo

Gráfico de los primeros cinco polinomios de

U n

Chebyshev del segundo tipo

Los primeros polinomios de Chebyshev del primer tipo en el dominio

-1 < x < 1

: El plano

T 0

T 1

T 2

T 3

T 4

T 5

Los primeros polinomios de Chebyshev del segundo tipo en el dominio

-1 < x < 1

: El plano

U 0

U 1

U 2

U 3

U 4

U 5

. Aunque no es visible en la imagen,

U n (1) = n + 1

U n (-1) = (n + 1)(-1) n

La función no suave (arriba)

y = - x 3 H (- x)

, donde

H

es la función escalón de Heaviside y (abajo) la quinta suma parcial de su expansión de Chebyshev. La séptima suma es indistinguible de la función original en la resolución del gráfico.