Gráfico hipohamiltoniano

No confundir con el gráfico hamiltoniano .

Un gráfico hipohamiltoniano construido por Lindgren (1967) .

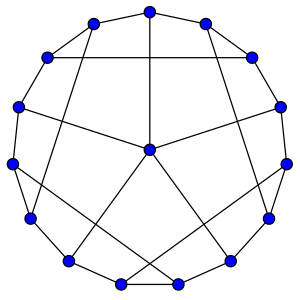
En el campo matemático de la teoría de grafos , se dice que un gráfico G es hipohamiltoniano si G no tiene un ciclo hamiltoniano, pero cada gráfico formado al eliminar un solo vértice de G es hamiltoniano .

Historia

Los gráficos hipohamiltonianos fueron estudiados por primera vez por Sousselier (1963) . Lindgren (1967) cita a Gaudin, Herz y Rossi (1964) y Busacker y Saaty (1965) como artículos iniciales adicionales sobre el tema; otro trabajo temprano es de Herz, Duby & Vigué (1967) .

Grötschel (1980) resume gran parte de la investigación en esta área con la siguiente oración: “Los artículos que tratan con esos gráficos ... usualmente exhiben nuevas clases de gráficos hipohamiltonianos o hipotraceables que muestran que para ciertos órdenes n tales gráficos existen o que poseen propiedades extrañas e inesperadas ".

Aplicaciones

Las gráficas hipohamiltonianas surgen en las soluciones de programación entera al problema del viajante de comercio: ciertos tipos de gráficas hipohamiltonianas definen las facetas del politopo del viajante , una forma definida como el casco convexo del conjunto de posibles soluciones al problema del viajante, y estas facetas pueden ser utilizado en métodos de plano de corte para resolver el problema. ^[1] Grötschel (1980) observa que la complejidad computacionalde determinar si una gráfica es hipohamiltoniana, aunque se desconoce, es probable que sea alta, lo que dificulta la búsqueda de facetas de estos tipos, excepto las definidas por pequeñas gráficas hipohamiltonianas; afortunadamente, los gráficos más pequeños conducen a las desigualdades más fuertes para esta aplicación. ^[2]

Park, Lim y Kim (2007) también han utilizado conceptos estrechamente relacionados con la hipohamiltonicidad para medir la tolerancia a fallos de las topologías de red para la computación en paralelo .

Propiedades

Cada grafo hipohamiltoniano debe estar conectado por 3 vértices , ya que la eliminación de dos vértices cualesquiera deja un camino hamiltoniano, que está conectado. Existen n gráficos hypohamiltonian -vertex en la que el grado máximo es de n / 2, y en el que hay aproximadamente n ² /4 bordes. ^[3]

Gráfico hipohamiltoniano de circunferencia 3 de Thomassen (1974b).

Herz, Duby & Vigué (1967) conjeturaron que cada grafo hipohamiltoniano tiene una circunferencia de 5 o más, pero esto fue refutado por Thomassen (1974b) , quien encontró ejemplos con circunferencia 3 y 4. Durante algún tiempo se desconocía si una grafica hipohamiltoniana podía ser planar , pero ahora se conocen varios ejemplos, ^[4] el más pequeño de los cuales tiene 40 vértices. ^[5] Cada grafo hipohamiltoniano plano tiene al menos un vértice con solo tres aristas incidentes. ^[6]

Si un gráfico de 3 regulares es hamiltoniano, sus bordes se pueden colorear con tres colores: use colores alternos para los bordes en el ciclo hamiltoniano (que debe tener una longitud uniforme según el lema del apretón de manos ) y un tercer color para todos los bordes restantes. Por lo tanto, todos los snarks , gráficos cúbicos sin puentes que requieren cuatro colores de borde, deben ser no hamiltonianos, y muchos snarks conocidos son hipohamiltonianos. Cada snark hipohamiltoniano es bicrítico : eliminar dos vértices cualesquiera deja un subgrafo cuyos bordes se pueden colorear con solo tres colores. ^[7]Un tricolor de este subgrafo se puede describir simplemente: después de eliminar un vértice, los vértices restantes contienen un ciclo hamiltoniano. Después de eliminar un segundo vértice, este ciclo se convierte en un camino, cuyos bordes se pueden colorear alternando entre dos colores. Los bordes restantes forman una combinación y se pueden colorear con un tercer color.

Las clases de color de cualquier color tridimensional de los bordes de un gráfico regular tridimensional forman tres coincidencias, de modo que cada borde pertenece exactamente a una de las coincidencias. Los snark hipohamiltonianos no tienen una partición en emparejamientos de este tipo, pero Häggkvist (2007) conjetura que los bordes de cualquier snark hipohamiltoniano pueden usarse para formar seis emparejamientos de modo que cada borde pertenezca exactamente a dos de los emparejamientos. Este es un caso especial de la conjetura de Berge-Fulkerson de que cualquier snark tiene seis coincidencias con esta propiedad.

Los gráficos hipohamiltonianos no pueden ser bipartitos: en un gráfico bipartito, un vértice solo se puede eliminar para formar un subgráfico hamiltoniano si pertenece a la mayor de las dos clases de color del gráfico. Sin embargo, cada gráfico bipartito se presenta como un subgráfico inducido de algún gráfico hipohamiltoniano. ^[8]

Ejemplos

El gráfico hipohamiltoniano más pequeño es el gráfico de Petersen ( Herz, Duby y Vigué 1967 ). De manera más general, el gráfico de Petersen generalizado GP ( n , 2) es hipohamiltoniano cuando n es 5 (mod 6); ^[9] el gráfico de Petersen es el ejemplo de esta construcción con n  = 5.

Lindgren (1967) encontró otra clase infinita de grafos hipohamiltonianos en los que el número de vértices es 4 (mod 6). La construcción de Lindgren consiste en un ciclo de longitud 3 (mod 6) y un solo vértice central; el vértice central está conectado a cada tercer vértice del ciclo por aristas que él llama radios, y los vértices a dos posiciones de cada extremo de radio están conectados entre sí. Nuevamente, la instancia más pequeña de la construcción de Lindgren es el gráfico de Petersen.

Bondy (1972) , Doyen y van Diest (1975) y Gutt (1977) proporcionan familias infinitas adicionales .

Enumeración

Václav Chvátal demostró en 1973 que para todo n suficientemente grande existe un grafo hipohamiltoniano con n vértices. Teniendo en cuenta los descubrimientos posteriores, ahora se sabe que ^[10] “suficientemente grande” significa que existen tales gráficas para todo n ≥ 18. Se conoce una lista completa de gráficas hipohamiltonianas con un máximo de 17 vértices: ^[11] son las 10- vértice gráfico de Petersen, un gráfico de 13 vértices y un gráfico de 15 vértices encontrados por búsquedas informáticas de Herz (1968) , y cuatro gráficos de 16 vértices. Existen al menos trece grafos hipohamiltonianos de 18 vértices. Aplicando el método flip-flop de Chvátal (1973) al gráfico de Petersen y al snark de flores, es posible mostrar que el número de grafos hipohamiltonianos, y más específicamente el número de snarks hipohamiltonianos, crece como una función exponencial del número de vértices. ^[12]

Generalizaciones

Los teóricos de grafos también han estudiado grafos hipotraceados , grafos que no contienen un camino hamiltoniano pero tales que cada subconjunto de n  - 1 vértices puede estar conectado por un camino. ^[13] Varios autores han considerado definiciones análogas de hipohamiltonicidad e hipotrazabilidad para gráficos dirigidos . ^[14]

Una definición equivalente de las gráficas hipohamiltonianas es que su ciclo más largo tiene una longitud n  - 1 y que la intersección de todos los ciclos más largos está vacía. Menke, Zamfirescu y Zamfirescu (1998) investigan gráficas con la misma propiedad de que la intersección de los ciclos más largos está vacía pero en las que la duración del ciclo más largo es más corta que n  - 1. Herz (1968) define la ciclabilidad de una gráfica como el número más grande k tal que cada k vértices pertenezca a un ciclo; las gráficas hipohamiltonianas son exactamente las gráficas que tienen ciclabilidad n  - 1. De manera similar, Park, Lim y Kim (2007) definen una gráfica como ƒ-falla hamiltoniana si la eliminación de como máximo ƒ vértices deja un subgrafo hamiltoniano. Schauerte y Zamfirescu (2006) estudian las gráficas con ciclabilidad n  - 2.

Notas

1. Grötschel (1977) ; Grötschel (1980) ; Grötschel y Wakabayashi (1981) .
2. Goemans (1995) .
3. Thomassen (1981) .
4. La existencia de grafos hipohamiltonianos planos fue planteada como una pregunta abierta por Chvátal (1973) , y Chvátal, Klarner & Knuth (1972) ofrecieron un premio de $ 5 por la construcción de uno. Thomassen (1976) utilizó el teorema de Grinberg para encontrar gráficas hipohamiltonianas planas de circunferencia 3, 4 y 5 y mostró que existen infinitas gráficas hipohamiltonianas planas.
5. Jooyandeh y col. (2013) , utilizando una búsqueda por computadora y el teorema de Grinberg. Wiener y Araya (2009) , Hatzel (1979) y Zamfirescu y Zamfirescu (2007) encontraron grafos hipohamiltonianos planos pequeños anteriores con 42, 57 y 48 vértices, respectivamente.
6. Thomassen (1978) .
7. Steffen (1998) ; Steffen (2001) .
8. Collier y Schmeichel (1977) .
9. Robertson (1969) demostró que estos gráficos no son hamiltonianos, mientras que es sencillo verificar que sus deleciones de un vértice son hamiltonianas. Ver Alspach (1983) para una clasificación de grafos de Petersen generalizados no hamiltonianos.
10. Thomassen (1974a) ; Doyen y van Diest (1975) .
11. Aldred, McKay y Wormald (1997) . Véase también (secuencia A141150 en la OEIS ).
12. Skupień (1989) ; Skupień (2007) .
13. Kapoor, Kronk y Lick (1968) ; Kronk (1969) ; Grünbaum (1974) ; Thomassen (1974a) .
14. Fouquet y Jolivet (1978) ; Grötschel y Wakabayashi (1980) ; Grötschel y Wakabayashi (1984) ; Thomassen (1978) .

Referencias

• Aldred, RA; McKay, BD ; Wormald, NC (1997), "Pequeños gráficos hipohamiltonianos" (PDF) , J. Combinatorial Math. Computación combinatoria. , 23 : 143-152 .
• Alspach, BR (1983), "La clasificación de los gráficos de Petersen generalizados de Hamilton", Journal of Combinatorial Theory, Serie B , 34 (3): 293–312, doi : 10.1016 / 0095-8956 (83) 90042-4 , MR  0714452 .
• Bondy, JA (1972), "Variaciones del tema hamiltoniano", Canadian Mathematical Bulletin , 15 : 57–62, doi : 10.4153 / CMB-1972-012-3.
• Busacker, RG; Saaty, TL (1965), Gráficos y redes finitos , McGraw-Hill.
• Chvátal, V. (1973), "Flip-flops in hypo-hamiltonian graphs", Canadian Mathematical Bulletin , 16 : 33–41, doi : 10.4153 / CMB-1973-008-9 , MR  0371722 .
• Chvátal, V .; Klarner, DA; Knuth, DE (1972), Problemas seleccionados de investigación combinatoria (PDF) , Tech. Informe STAN-CS-72-292, Departamento de Ciencias de la Computación, Universidad de Stanford .
• Collier, JB; Schmeichel, EF (1977), "Nuevas construcciones de flip-flop para gráficos hipohamiltonianos", Matemáticas discretas , 18 (3): 265-271, doi : 10.1016 / 0012-365X (77) 90130-3 , MR  0543828.
• Doyen, J .; van Diest, V. (1975), "Nuevas familias de gráficos hipohamiltonianos", Matemáticas discretas , 13 (3): 225-236, doi : 10.1016 / 0012-365X (75) 90020-5 , MR  0416979.
• Fouquet, J.-L .; Jolivet, JL (1978), "Gráficos orientados hipohamiltonianos", Cahiers Centre Études Rech. Opér. , 20 (2): 171–181, MR  0498218.
• Gaudin, T .; Herz, P .; Rossi (1964), "Solution du problème No. 29", Rev. Franç. Rech. Opérationnelle , 8 : 214–218.
• Goemans, Michel X. (1995), "Comparación del peor caso de desigualdades válidas para el TSP", Programación matemática , 69 (1-3): 335-349, CiteSeerX  10.1.1.52.8008 , doi : 10.1007 / BF01585563.
• Grötschel, M. (1977), "Facetas hipohamiltonianas del politopo simétrico del viajante", Zeitschrift für Angewandte Mathematik und Mechanik , 58 : 469–471 .
• Grötschel, M. (1980), "Sobre el problema monótono y simétrico del viajante: gráficas y facetas hipohamiltonianas / hipotraceables", Mathematics of Operations Research , 5 (2): 285-292, doi : 10.1287 / moor.5.2.285 , JSTOR  3689157 .
• Grötschel, M .; Wakabayashi, Y. (1980), "Dígrafos hipohamiltonianos", Métodos de investigación de operaciones , 36 : 99-119, Zbl  0436.05038.
• Grötschel, M .; Wakabayashi, Y. (1981), "Sobre la estructura del politopo I monótono y asimétrico del viajante: facetas hipohamiltonianas", Matemáticas discretas , 24 : 43–59, doi : 10.1016 / 0012-365X (81) 90021-2.
• Grötschel, M .; Wakabayashi, Y. (1984), "Construcciones de dígrafos hipotraceables", en Cottle, RW; Kelmanson, ML; Korte, B. (eds.), Programación Matemática (Proc. Congreso Internacional, Río de Janeiro, 1981) , Holanda Septentrional.
• Grünbaum, B. (1974), "Vértices perdidos por trayectos o circuitos más largos", Journal of Combinatorial Theory, Serie A , 17 : 31–38, doi : 10.1016 / 0097-3165 (74) 90025-9 , MR  0349474 .
• Gutt, Simone (1977), "Familias infinitas de grafos hipohamiltonianos", Académie Royale de Belgique, Bulletin de la Classe des Sciences , 5e Série, 63 (5): 432–440, MR  0498243 .
• Häggkvist, R. (2007), Mohar, B .; Nowakowski, RJ; West, DB (eds.), "Problema 443. Caso especial de la conjetura de Fulkerson", Problemas de investigación de la Quinta Conferencia de Eslovenia (Bled, 2003), Matemáticas discretas , 307 (3-5): 650-658, doi : 10.1016 /j.disc.2006.07.013.
• Hatzel, W. (1979), "Ein planarer hypohamiltonscher Graph mit 57 Knoten", Math. Ana. , 243 (3): 213–216, doi : 10.1007 / BF01424541 , MR  0548801.
• Herz, JC (1968), "Sur la cyclabilité des graphes", Computers in Mathematical Research , Holanda Septentrional, págs. 97-107, MR  0245461.
• Herz, JC; Duby, JJ; Vigué, F. (1967), "Recherche systématique des graphes hypohamiltoniens", en Rosenstiehl, P. (ed.), Theory of Graphs: International Symposium, Roma 1966 , París: Gordon and Breach, págs. 153-159.
• Jooyandeh, Mohammadreza; McKay, Brendan D .; Östergård, Patric RJ; Pettersson, Ville H .; Zamfirescu, Carol T. (2013), Gráficos planos hipohamiltonianos en 40 vértices , arXiv : 1302.2698 , Bibcode : 2013arXiv1302.2698J .
• Kapoor, SF; Kronk, HV; Lick, DR (1968), "Sobre desvíos en gráficos", Canadian Mathematical Bulletin , 11 (2): 195-201, doi : 10.4153 / CMB-1968-022-8 , MR  0229543.
• Kronk, HV (1969), Klee, V. (ed.), "Does there exist a hypotraceable graph?", Research Problems, American Mathematical Monthly , 76 (7): 809–810, doi : 10.2307 / 2317879 , JSTOR  2317879.
• Lindgren, WF (1967), "Una clase infinita de gráficos hipohamiltonianos", American Mathematical Monthly , 74 (9): 1087–1089, doi : 10.2307 / 2313617 , JSTOR  2313617 , MR  0224501.
• Máčajová, E .; Škoviera, M. (2007), "Construyendo snarks hipohamiltonianos con conectividad cíclica 5 y 6" , Electronic Journal of Combinatorics , 14 (1): R14.
• Menke, B .; Zamfirescu, TI; Zamfirescu, CM (1998), "Intersecciones de ciclos más largos en gráficos de cuadrícula", Journal of Graph Theory , 25 (1): 37–52, doi : 10.1002 / (SICI) 1097-0118 (199705) 25: 1 <37: : AID-JGT2> 3.0.CO; 2-J.
• Mohanty, SP; Rao, D. (1981), "Una familia de prismas generalizados hipo-hamiltonianos", Combinatoria y teoría de grafos , Lecture Notes in Mathematics, 885 , Springer-Verlag, págs. 331–338, doi : 10.1007 / BFb0092278 , ISBN 978-3-540-11151-1.
• Park, J.-H .; Lim, H.-S .; Kim, H.-C. (2007), "Panconectividad y panciclicidad de redes de interconexión tipo hipercubo con elementos defectuosos", Informática teórica , 377 (1-3): 170-180, doi : 10.1016 / j.tcs.2007.02.029.
• Robertson, GN (1969), Gráficos mínimos bajo circunferencia, valencia y restricciones de conectividad , tesis de doctorado, Waterloo, Ontario: Universidad de Waterloo.
• Schauerte, Boris; Zamfirescu, CT (2006), "Gráficos regulares en los que cada par de puntos se pierde por algún ciclo más largo", An. Univ. Craiova Ser. Estera. Informar. , 33 : 154-173, hdl : 1854 / LU-6901462 , MR  2359901.
• Skupień, Z. (1989), "Exponencialmente muchas gráficas hipohamiltonianas", Gráficas, Hipergrafías y Matroides III (Proc. Conf. Kalsk 1988) , Zielona Góra: Escuela Superior de Ingeniería, págs. 123-132 . Como lo cita Skupień (2007) .
• Skupień, Z. (2007), "Exponentially many hypohamiltonian snarks", VI Simposio internacional checo-eslovaco sobre combinatoria, teoría de grafos, algoritmos y aplicaciones , notas electrónicas en matemáticas discretas, 28 , págs. 417–424, doi : 10.1016 / j .endm.2007.01.059.
• Sousselier, R. (1963), Berge, C. (ed.), "Problème n. ° 29: Le cercle des irascibles", Problèmes plaisants et délectables, Rev. Franç. Rech. Opérationnelle , 7 : 405–406.
• Steffen, E. (1998), "Clasificación y caracterizaciones de snarks", Matemáticas discretas , 188 (1-3): 183-203, doi : 10.1016 / S0012-365X (97) 00255-0 , MR  1630478.
• Steffen, E. (2001), "Sobre los sarcasmos bicríticos", Math. Eslovaca , 51 (2): 141-150, MR  1841443.
• Thomassen, Carsten (1974a), "Gráficas hipohamiltonianas e hipotraceables", Matemáticas discretas , 9 : 91–96, doi : 10.1016 / 0012-365X (74) 90074-0 , MR  0347682 .
• Thomassen, Carsten (1974b), "Sobre gráficas hipohamiltonianas", Matemáticas discretas , 10 (2): 383–390, doi : 10.1016 / 0012-365X (74) 90128-9 , MR  0357226 .
• Thomassen, Carsten (1976), "Gráficos planos e infinitos hipohamiltonianos e hipotraceables", Matemáticas discretas , 14 (4): 377–389, doi : 10.1016 / 0012-365X (76) 90071-6 , MR  0422086 .
• Thomassen, Carsten (1978), "Gráficos y dígrafos hipohamiltonianos", Teoría y aplicaciones de los gráficos (Proc. Internat. Conf., Western Mich. Univ., Kalamazoo, Mich., 1976) , Lecture Notes in Mathematics, 642 , Berlín: Springer-Verlag, págs. 557–571, MR  0499523 .
• Thomassen, Carsten (1981), " Gráficas planas cúbicas hipo-hamiltonianas e hipotraceables", Journal of Combinatorial Theory, Serie B , 30 : 36–44, doi : 10.1016 / 0095-8956 (81) 90089-7 , MR  0609592 .
• Wiener, Gábor; Araya, Makoto (2009), The ultimate question , arXiv : 0904.3012 , Bibcode : 2009arXiv0904.3012W.
• Zamfirescu, CT; Zamfirescu, TI (2007), "Un gráfico hipohamiltoniano plano con 48 vértices", Journal of Graph Theory , 55 (4): 338–342, doi : 10.1002 / jgt.20241.

Enlaces externos

• Weisstein, Eric W. , "Gráfico hipohamiltoniano" , MathWorld