Árbol de extensión

Árbol de extensión
Escribe	árbol
Inventado	1985
Inventado por	Daniel Dominic Sleator y Robert Endre Tarjan
Complejidad del tiempo en notación O grande
Algoritmo Promedio Peor de los casos Espacio O ( n ) O ( n ) Buscar amortizado O (log n ) amortizado O (log n ) Insertar amortizado O (log n ) amortizado O (log n ) Borrar amortizado O (log n ) amortizado O (log n )

Un árbol de splay es un árbol de búsqueda binario con la propiedad adicional de que los elementos a los que se ha accedido recientemente son de acceso rápido de nuevo. Al igual que los árboles de búsqueda binaria autoequilibrados , un árbol de distribución realiza operaciones básicas como la inserción, búsqueda y eliminación en el tiempo amortizado O (log n ) . Para muchas secuencias de operaciones no aleatorias, los árboles de splay funcionan mejor que otros árboles de búsqueda, incluso funcionan mejor que O (log n ) para patrones suficientemente no aleatorios, todo sin requerir un conocimiento previo del patrón. El árbol de extensión fue inventado por Daniel Sleator y Robert Tarjan en 1985. ^[1]

Todas las operaciones normales en un árbol de búsqueda binaria se combinan con una operación básica, llamada splaying . Extender el árbol para un determinado elemento reorganiza el árbol para que el elemento se coloque en la raíz del árbol. Una forma de hacer esto con la operación de búsqueda básica es realizar primero una búsqueda de árbol binario estándar para el elemento en cuestión y luego usar rotaciones de árbol de una manera específica para llevar el elemento a la parte superior. Alternativamente, un algoritmo de arriba hacia abajo puede combinar la búsqueda y la reorganización del árbol en una sola fase.

Ventajas

El buen rendimiento de un árbol de distribución depende del hecho de que se optimiza automáticamente, ya que los nodos a los que se accede con frecuencia se acercarán a la raíz, donde se puede acceder a ellos más rápidamente. La altura en el peor de los casos, aunque poco probable, es O ( n ), siendo el promedio O (log n ). Tener nodos de uso frecuente cerca de la raíz es una ventaja para muchas aplicaciones prácticas (ver también la localidad de referencia ) y es particularmente útil para implementar cachés y algoritmos de recolección de basura .

Las ventajas incluyen:

• Rendimiento comparable: el rendimiento promedio de casos es tan eficiente como otros árboles. ^[2]
• Pequeña huella de memoria: los árboles de Splay no necesitan almacenar ningún dato contable.

Desventajas

La desventaja más significativa de los árboles esparcidos es que la altura de un árbol esparcido puede ser lineal. Por ejemplo, este será el caso después de acceder a todos los n elementos en orden no decreciente. Dado que la altura de un árbol corresponde al tiempo de acceso en el peor de los casos, esto significa que el costo real de una sola operación puede ser alto. Sin embargo, el costo de acceso amortizado de este peor caso es logarítmico, O (log n ). Además, el costo de acceso esperado se puede reducir a O (log n ) mediante el uso de una variante aleatoria. ^[3]

La representación de los árboles de splay puede cambiar incluso cuando se accede a ellos de forma de "sólo lectura" (es decir, mediante operaciones de búsqueda ). Esto complica el uso de tales árboles de extensión en un entorno de subprocesos múltiples. Específicamente, se necesita una administración adicional si se permite que varios subprocesos realicen operaciones de búsqueda al mismo tiempo. Esto también los hace inadecuados para uso general en programación puramente funcional, aunque incluso allí se pueden usar de manera limitada para implementar colas de prioridad.

Finalmente, cuando el patrón de acceso es aleatorio, la sobrecarga de distribución adicional agrega un factor constante significativo al costo en comparación con las alternativas menos dinámicas.

Operaciones

Desplegando

Cuando se accede a un nodo x , se realiza una operación de extensión en x para moverlo a la raíz. Para realizar una operación de extensión, llevamos a cabo una secuencia de pasos de extensión , cada uno de los cuales se acerca x a la raíz. Al realizar una operación de distribución en el nodo de interés después de cada acceso, los nodos a los que se accedió recientemente se mantienen cerca de la raíz y el árbol permanece aproximadamente equilibrado, de modo que logramos los límites de tiempo de amortización deseados.

Cada paso en particular depende de tres factores:

• Si x es el hijo izquierdo o derecho de su nodo padre, p ,
• si p es la raíz o no, y si no
• si p es el hijo izquierdo o derecho de su padre, g (el abuelo de x).

Es importante recordar configurar gg (el bisabuelo de x) para que ahora apunte ax después de cualquier operación de splay. Si gg es nulo, entonces x obviamente ahora es la raíz y debe actualizarse como tal.

Hay tres tipos de pasos de apertura, cada uno de los cuales tiene dos variantes simétricas: para zurdos y para diestros. En aras de la brevedad, solo se muestra uno de estos dos para cada tipo. (En los siguientes diagramas, los círculos indican nodos de interés y los triángulos indican subárboles de tamaño arbitrario). Los tres tipos de pasos de extensión son:

Paso Zig: este paso se realiza cuando p es la raíz. El árbol se hace girar en el borde entre x y p . Los pasos de Zig existen para tratar el problema de la paridad, se realizarán solo como el último paso en una operación de separación, y solo cuando x tenga una profundidad impar al comienzo de la operación.

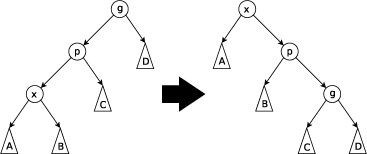
Zig-zig paso: este paso se realiza cuando p no es la raíz y x y p son ambos hijos son correctos o ambos hijos izquierda. La siguiente imagen muestra el caso en el que x y p son ambos hijos dejados. El árbol se gira en el borde que une p con su padre g , luego se gira en el borde que une x con p . Tenga en cuenta que los pasos en zig-zig son lo único que diferencia a los árboles de expansión del método de rotación a raíz introducido por Allen y Munro ^[4] antes de la introducción de los árboles de expansión.

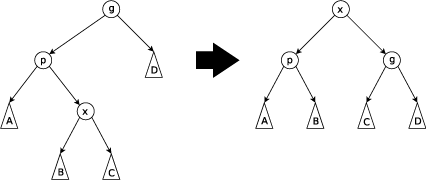
Paso en zig-zag: este paso se realiza cuando p no es la raíz y x es un hijo derecho yp es un hijo izquierdo o viceversa. El árbol se gira en el borde entre p y x, y luego se gira en el borde resultante entre x y g.

Entrar

Dados dos árboles S y T tales que todos los elementos de S son más pequeños que los elementos de T, se pueden usar los siguientes pasos para unirlos a un solo árbol:

• Extienda el elemento más grande en S. Ahora este elemento está en la raíz de S y tiene un hijo derecho nulo.
• Establezca el hijo correcto de la nueva raíz en T.

Separar

Dado un árbol y un elemento x , devuelve dos árboles nuevos: uno que contiene todos los elementos menores o iguales ax y el otro que contiene todos los elementos mayores que x . Esto se puede hacer de la siguiente manera:

• Splay x . Ahora está en la raíz, por lo que el árbol a su izquierda contiene todos los elementos menores que x y el árbol a su derecha contiene todos los elementos mayores que x .
• Divida el subárbol derecho del resto del árbol.

Inserción

Para insertar un valor x en un árbol de distribución:

• Inserte x como con un árbol de búsqueda binario normal .
• cuando se inserta un elemento, se realiza una expansión.
• Como resultado, el nodo x recién insertado se convierte en la raíz del árbol.

Alternativamente:

• Utilice la operación de división para dividir el árbol al valor de x en dos subárboles: S y T.
• Cree un nuevo árbol en el que x es la raíz, S es su subárbol izquierdo y T es su subárbol derecho.

Supresión

Para eliminar un nodo x , use el mismo método que con un árbol de búsqueda binaria:

• Si x tiene dos hijos:
  • Cambie su valor con el del nodo más a la derecha de su subárbol izquierdo (su predecesor en orden) o el nodo más a la izquierda de su subárbol derecho (su sucesor en orden).
  • En su lugar, elimine ese nodo.

De esta forma, la eliminación se reduce al problema de eliminar un nodo con 0 o 1 hijos. A diferencia de un árbol de búsqueda binaria, en un árbol de distribución después de la eliminación, colocamos el padre del nodo eliminado en la parte superior del árbol.

Alternativamente:

• El nodo que se va a eliminar se abre primero, es decir, se lleva a la raíz del árbol y luego se elimina. deja el árbol con dos subárboles.
• A continuación, los dos subárboles se unen mediante una operación de "unión".

Implementación y variantes

La propagación, como se mencionó anteriormente, se realiza durante una segunda pasada de abajo hacia arriba sobre la ruta de acceso de un nodo. Es posible registrar la ruta de acceso durante la primera pasada para usarla durante la segunda, pero eso requiere espacio adicional durante la operación de acceso. Otra alternativa es mantener un puntero principal en cada nodo, lo que evita la necesidad de espacio adicional durante las operaciones de acceso, pero puede reducir la eficiencia general del tiempo debido a la necesidad de actualizar esos punteros. ^[1]

Otro método que se puede utilizar se basa en el argumento de que podemos reestructurar el árbol en nuestro camino por la ruta de acceso en lugar de hacer una segunda pasada. Esta rutina de distribución de arriba hacia abajo utiliza tres conjuntos de nodos: árbol de la izquierda, árbol de la derecha y árbol del medio. Los dos primeros contienen todos los elementos del árbol original que se sabe que son menores o mayores que el elemento actual, respectivamente. El árbol del medio consiste en el subárbol enraizado en el nodo actual. Estos tres conjuntos se actualizan a lo largo de la ruta de acceso mientras se mantienen controladas las operaciones de distribución. Otro método, semisplaying, modifica el caso en zig-zig para reducir la cantidad de reestructuración realizada en todas las operaciones. ^{[1] [5]}

A continuación, se muestra una implementación de árboles de distribución en C ++, que utiliza punteros para representar cada nodo del árbol. Esta implementación se basa en la versión de distribución ascendente y utiliza el segundo método de eliminación en un árbol de distribución. Además, a diferencia de la definición anterior, esta versión de C ++ no extiende el árbol en los hallazgos, solo se muestra en las inserciones y eliminaciones, y la operación de búsqueda, por lo tanto, tiene una complejidad de tiempo lineal.

#include <funcional> #ifndef SPLAY_TREE #define SPLAY_TREEplantilla < typename  T , typename Comp = std :: less < T >>    class  splay_tree { privado : Comp comp ;  unsigned long p_size ;    struct  nodo {  nodo * izquierda , * derecha ;   nodo * padre ;  Tecla T ;  nodo ( const T & init = T ()) : izquierda ( nullptr ), derecha ( nullptr ), padre ( nullptr ), clave ( init ) { }            ~ nodo () {  } } * raíz ;   void left_rotate ( nodo * x ) {    nodo * y = x -> derecha ;    si ( y ) {   x -> derecha = y -> izquierda ;   if ( y -> left ) y -> left -> parent = x ;     y -> padre = x -> padre ;   }  if ( ! x -> padre ) root = y ;     otra cosa si ( x == x -> padres -> izquierda ) x -> padres -> izquierda = y ;        si no x -> padre -> derecha = y ;    si ( y ) y -> izquierda = x ;     x -> padre = y ;   }  void right_rotate ( nodo * x ) {    nodo * y = x -> izquierda ;    si ( y ) {   x -> izquierda = y -> derecha ;   if ( y -> derecha ) y -> derecha -> padre = x ;     y -> padre = x -> padre ;   } if ( ! x -> padre ) root = y ;     otra cosa si ( x == x -> padres -> izquierda ) x -> padres -> izquierda = y ;        si no x -> padre -> derecha = y ;    si ( y ) y -> derecha = x ;     x -> padre = y ;   }  espacio vacío ( nodo * x ) {    while ( x -> padre ) {   if ( ! x -> padre -> padre ) {   if ( x -> padre -> izquierda == x ) right_rotate ( x -> padre );     else left_rotate ( x -> padre );  } más si ( x -> padre -> izquierda == x && x -> padre -> padre -> izquierda == x -> padre ) {           right_rotate ( x -> padre -> padre ); right_rotate ( x -> padre ); } más si ( x -> padre -> derecha == x && x -> padre -> padre -> derecha == x -> padre ) {           left_rotate ( x -> padre -> padre ); left_rotate ( x -> padre ); } más si ( x -> padre -> izquierda == x && x -> padre -> padre -> derecha == x -> padre ) {           right_rotate ( x -> padre ); left_rotate ( x -> padre ); } más {   left_rotate ( x -> padre ); right_rotate ( x -> padre ); } } }  reemplazo vacío ( nodo * u , nodo * v ) {      if ( ! u -> padre ) root = v ;     otra cosa si ( u == U -> padres -> izquierda ) u -> padres -> izquierda = v ;        si no u -> padre -> derecha = v ;    si ( v ) v -> padre = u -> padre ;     }  nodo * subtree_minimum ( nodo * u ) {    while ( u -> izquierda ) u = u -> izquierda ;     return u ;  }  nodo * subtree_maximum ( nodo * u ) {    while ( u -> derecha ) u = u -> derecha ;     return u ;  }publico : splay_tree () : raíz ( nullptr ), p_size ( 0 ) { }       inserto vacío ( const T & clave ) {     nodo * z = raíz ;    nodo * p = nullptr ;     while ( z ) {   p = z ;   if ( comp ( z -> tecla , tecla )) z = z -> derecha ;      si no z = z -> izquierda ;    }  z = nuevo nodo ( clave );    z -> padre = p ;    si ( ! p ) raíz = z ;     otra cosa si ( borrador ( p -> llave , z -> clave )) p -> derecha = z ;       si no p -> izquierda = z ;     esparcimiento ( z ); p_size ++ ; }  nodo * buscar ( const T & clave ) {     nodo * z = raíz ;    while ( z ) {   if ( comp ( z -> tecla , tecla )) z = z -> derecha ;      de lo contrario si ( comp ( tecla , z -> tecla )) z = z -> izquierda ;       de lo contrario, devuelve z ;   } return nullptr ;  }  borrado vacío ( tecla T y constante ) {     nodo * z = buscar ( clave );    if ( ! z ) return ;    esparcimiento ( z );  si ( ! z -> izquierda ) reemplazar ( z , z -> derecha );    otra cosa si ( ! z -> derecha ) reemplazar a ( z , z -> izquierda );     else {  nodo * y = subtree_minimum ( z -> derecha );    if ( y -> padre ! = z ) {     reemplazar ( y , y -> derecha );  y -> derecha = z -> derecha ;   y -> derecha -> padre = y ;   } reemplazar ( z , y );  y -> izquierda = z -> izquierda ;   y -> izquierda -> padre = y ;   }  eliminar z ;  p_size - ; }/ * // la implementación alternativa  void erase (const T & key) {  node * z = find (key);  if (! z) return;  esparcimiento (z);  nodo * s = z-> izquierda;  nodo * t = z-> derecha;  eliminar z;  nodo * sMax = NULL;  if (s) {  s-> parent = NULL;  sMax = subtree_maximum (s);  splay (sMax);  root = sMax;  }  if (t) {  if (s)  sMax-> right = t;  si no  root = t;  t-> padre = sMax;  }  p_size--;  }    * /  const T & mínima () { return subtree_minimum ( raíz ) -> clave ; }       const T & maximum () { return subtree_maximum ( raíz ) -> clave ; }        bool vacío () const { return root == nullptr ; }         unsigned long size () const { return p_size ; }       };#endif // SPLAY_TREE

Análisis

Se puede realizar un análisis simple amortizado de árboles de distribución estática utilizando el método de potencial . Definir:

• tamaño ( r ) = el número de nodos en el subárbol enraizados en el nodo r (incluido r ).
• rango ( r ) = log ₂ (tamaño ( r )).
• Φ = la suma de los rangos de todos los nodos del árbol.

Φ tenderá a ser alto para árboles mal equilibrados y bajo para árboles bien equilibrados.

Para aplicar el método del potencial , primero calculamos ΔΦ: el cambio en el potencial causado por una operación de expansión. Revisamos cada caso por separado. Denote por rango ′ la función de rango después de la operación. x, pyg son los nodos afectados por la operación de rotación (ver figuras arriba).

Paso en zig

ΔΦ	= rango ′ ( p ) - rango ( p ) + rango ′ ( x ) - rango ( x )	[ya que solo pyx cambian de rango]
	= rango ′ ( p ) - rango ( x )	[desde rango ′ ( x ) = rango ( p )]
	≤ rango ′ ( x ) - rango ( x )	[desde rango ′ ( p ) <rango ′ ( x )]

Paso en zig-zig

ΔΦ	= rango ′ ( g ) - rango ( g ) + rango ′ ( p ) - rango ( p ) + rango ′ ( x ) - rango ( x )
	= rango ′ ( g ) + rango ′ ( p ) - rango ( p ) - rango ( x )	[desde rango ′ (x) = rango (g)]
	≤ rango ′ ( g ) + rango ′ ( x ) - 2 rango ( x )	[ya que rango ( x ) <rango ( p ) y rango ′ ( x )> rango ′ ( p )]
	≤ 3 (rango ′ ( x ) −rank ( x )) - 2	[debido a la concavidad de la función de registro]

Paso en zig-zag

ΔΦ	= rango ′ ( g ) - rango ( g ) + rango ′ ( p ) - rango ( p ) + rango ′ ( x ) - rango ( x )
	≤ rango ′ ( g ) + rango ′ ( p ) - 2 rango ( x )	[ya que rango ′ ( x ) = rango ( g ) y rango ( x ) <rango ( p )]
	≤ 3 (rango ′ ( x ) −rank ( x )) - 2	[debido a la concavidad de la función de registro]

El costo amortizado de cualquier operación es ΔΦ más el costo real. El costo real de cualquier operación en zig-zig o zig-zag es 2 ya que hay dos rotaciones para realizar. Por eso:

coste amortizado	= costo + ΔΦ
	≤ 3 (rango ′ ( x ) −rango ( x ))

Cuando sumada sobre toda la operación splay, este telescopios a 3 (rango (raíz) -rank ( x )), que es O (log n ). La operación Zig agrega un costo amortizado de 1, pero hay como máximo una operación de este tipo.

Entonces ahora sabemos que el tiempo total amortizado para una secuencia de m operaciones es:

${\displaystyle T_{\mathrm {amortized} }(m)=O(m\log n)}$

Para pasar del tiempo amortizado al tiempo real, debemos sumar la disminución del potencial desde el estado inicial antes de que se realice cualquier operación (Φ _i ) al estado final después de que se hayan completado todas las operaciones (Φ _f ).

${\displaystyle \Phi _{i}-\Phi _{f}=\sum _{x}{\mathrm {rank} _{i}(x)-\mathrm {rank} _{f}(x)}=O(n\log n)}$

donde la última desigualdad proviene del hecho de que para cada nodo x , el rango mínimo es 0 y el rango máximo es log ( n ).

Ahora finalmente podemos acotar el tiempo real:

${\displaystyle T_{\mathrm {actual} }(m)=O(m\log n+n\log n)}$

Análisis ponderado

El análisis anterior se puede generalizar de la siguiente manera.

• Asigne a cada nodo r un peso w ( r ).
• Definir tamaño ( r ) = la suma de los pesos de los nodos en el subárbol enraizado en el nodo r (incluido r ).
• Defina el rango ( r ) y Φ exactamente como se indicó anteriormente.

Se aplica el mismo análisis y el costo amortizado de una operación de distribución es nuevamente:

${\displaystyle \mathrm {rank} (root)-\mathrm {rank} (x)=O(\log {W}-\log {w(x)})=O\left(\log {\frac {W}{w(x)}}\right)}$

donde W es la suma de todos los pesos.

La disminución del potencial inicial al final está limitada por:

${\displaystyle \Phi _{i}-\Phi _{f}\leq \sum _{x\in tree}{\log {\frac {W}{w(x)}}}}$

ya que el tamaño máximo de cualquier nodo es W y el mínimo es w (x) .

Por lo tanto, el tiempo real está limitado por:

${\displaystyle O\left(\sum _{x\in sequence}{\log {\frac {W}{w(x)}}}+\sum _{x\in tree}{\log {\frac {W}{w(x)}}}\right)}$

Teoremas de desempeño

Hay varios teoremas y conjeturas con respecto al tiempo de ejecución en el peor de los casos para realizar una secuencia de S de m accesos en un árbol de distribución que contiene n elementos.

Teorema del equilibrio  :  el costo de realizar la secuencia S es .${\displaystyle O\left[m\log n+n\log n\right]}$

Prueba  -

Tome un peso constante, por ejemplo, para cada nodo x . Entonces .${\displaystyle w(x)=1}$${\displaystyle W=n}$

Este teorema implica que los árboles de distribución funcionan tan bien como los árboles de búsqueda binarios balanceados estáticos en secuencias de al menos n accesos. ^[1]

Estático optimalidad Teorema  -  Dejado sea el número de veces elemento x se accede en S . Si se accede a cada elemento al menos una vez, entonces el costo de realizar S es${\displaystyle q_{x}}$${\displaystyle O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]}$

Prueba  -

Deja . Entonces .${\displaystyle w(x)=q_{x}}$${\displaystyle W=m}$

Este teorema implica que los árboles de distribución funcionan tan bien como un árbol de búsqueda binario estático óptimo en secuencias de al menos n accesos. Dedican menos tiempo a los elementos más frecuentes. ^[1]

Teorema del dedo estático  :  suponga que los elementos están numerados del 1 al n en orden ascendente. Sea f cualquier elemento fijo (el 'dedo'). Entonces el costo de realizar S es .${\displaystyle O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]}$

Prueba  -

Deja . Entonces . La caída de potencial neta es O ( n log n ) ya que el peso de cualquier artículo es al menos . ^[1]${\displaystyle w(x)=1/(|x-f|+1)^{2}}$${\displaystyle W=O(1)}$${\displaystyle 1/n^{2}}$

Teorema dinámico del dedo  :  suponga que el 'dedo' para cada paso que accede a un elemento y es el elemento al que se accede en el paso anterior, x . El costo de realizar S es . ^{[6] [7]}${\displaystyle O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]}$

Teorema del conjunto de trabajo  :  en cualquier momento durante la secuencia, sea ​​el número de elementos distintos a los que se accedió antes de que se accediera al elemento de tiempo x anterior. El costo de realizar S es${\displaystyle t(x)}$${\displaystyle O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]}$

Prueba  -

Deja . Tenga en cuenta que aquí los pesos cambian durante la secuencia. Sin embargo, la secuencia de pesos sigue siendo una permutación de . Así como antes . La caída de potencial neta es O ( n log n ).${\displaystyle w(x)=1/(t(x)+1)^{2}}$${\displaystyle 1,{\tfrac {1}{4}},{\tfrac {1}{9}},\cdots ,{\tfrac {1}{n^{2}}}}$${\displaystyle W=O(1)}$

Este teorema es equivalente a árboles de splay que tienen una optimización independiente de la clave . ^[1]

Teorema de exploración  :  también conocido como teorema de acceso secuencial o teorema de cola . Acceder a los n elementos de un árbol de distribución en orden simétrico lleva O ( n ) tiempo, independientemente de la estructura inicial del árbol de distribución. ^[8] El límite superior más estricto probado hasta ahora es . ^[9]${\displaystyle 4.5n}$

Conjetura de optimalidad dinámica

Artículo principal: árbol de búsqueda binario óptimo

Problema no resuelto en informática :

¿Los árboles de splay funcionan tan bien como cualquier otro algoritmo de árbol de búsqueda binario?

(más problemas sin resolver en informática)

Además de las garantías de rendimiento comprobadas para los árboles de splay, existe una conjetura no probada de gran interés del documento original de Sleator y Tarjan. Esta conjetura se conoce como conjetura de optimización dinámica y básicamente afirma que los árboles de splay funcionan tan bien como cualquier otro algoritmo de árbol de búsqueda binaria hasta un factor constante.

Conjetura de Optimidad Dinámica: ^[1] Sea cualquier algoritmo de árbol de búsqueda binario que acceda a un elemento atravesando la ruta desde la raíz hasta a un costo de , y que entre accesos pueda hacer cualquier rotación en el árbol a un costo de 1 por rotación. Sea el coste de realizar la secuencia de accesos. Entonces, el costo de un árbol de distribución para realizar los mismos accesos es .${\displaystyle A}$${\displaystyle x}$${\displaystyle x}$${\displaystyle d(x)+1}$${\displaystyle A(S)}$${\displaystyle A}$${\displaystyle S}$${\displaystyle O[n+A(S)]}$

Hay varios corolarios de la conjetura de la optimización dinámica que aún no se han probado:

Conjetura transversal: ^[1] Sean y dos árboles esparcidos que contienen los mismos elementos. Sea la secuencia obtenida visitando los elementos en preorden (es decir, primer orden de búsqueda en profundidad). El coste total de realizar la secuencia de accesos en es .${\displaystyle T_{1}}$${\displaystyle T_{2}}$${\displaystyle S}$${\displaystyle T_{2}}$${\displaystyle S}$${\displaystyle T_{1}}$${\displaystyle O(n)}$

Conjetura de Deque: ^{[8] [10] [11]} Sea una secuencia de operaciones de cola de dos extremos (empujar, hacer estallar, inyectar, expulsar). Entonces el costo de actuar en un árbol de splay es .${\displaystyle S}$${\displaystyle m}$ ${\displaystyle S}$${\displaystyle O(m+n)}$

Conjetura dividida: ^[5] Sea cualquier permutación de los elementos del árbol de distribución. Entonces el costo de eliminar los elementos en el pedido es .${\displaystyle S}$${\displaystyle S}$${\displaystyle O(n)}$

Variantes

Con el fin de reducir el número de operaciones de reestructuración, es posible reemplazar el esparcimiento por semiseparado , en el que un elemento se esparce solo hasta la mitad de la raíz. ^{[1] [12]}

Otra forma de reducir la reestructuración es hacer una distribución completa, pero solo en algunas de las operaciones de acceso, solo cuando la ruta de acceso es más larga que un umbral, o solo en las primeras m operaciones de acceso. ^[1]

Ver también

• Árbol de dedos
• Enlace / árbol cortado
• Árbol de chivo expiatorio
• Cremallera (estructura de datos)
• Árboles
• Rotación de árboles
• Árbol AVL
• Árbol B
• Árbol en T
• Lista de estructuras de datos
• Estructura del conjunto de trabajo de Iacono
• Geometría de árboles de búsqueda binarios
• Splaysort , un algoritmo de clasificación que utiliza árboles de distribución
• Treap

Notas

1. Sleator y Tarjan 1985 .
2. Goodrich, Tamassia y Goldwasser 2014 .
3. Albers y Karpinski 2002 .
4. Allen y Munro 1978 .
5. Lucas, 1991 .
6. Cole y col. 2000 .
7. Cole 2000 .
8. Tarjan, 1985 .
9. Elmasry 2004 .
10. Pettie 2008 .
11. Sundar 1992 .
12. Brinkmann, Degraer y De Loof 2009 .

Referencias

• Albers, Susanne; Karpinski, Marek (28 de febrero de 2002). "Árboles de distribución aleatoria: resultados teóricos y experimentales" (PDF) . Cartas de procesamiento de información . 81 (4): 213-221. doi : 10.1016 / s0020-0190 (01) 00230-7 .

• Allen, Brian; Munro, Ian (octubre de 1978). "Árboles de búsqueda binarios autoorganizados". Revista de la ACM . 25 (4): 526–535. doi : 10.1145 / 322092.322094 . S2CID  15967344 .

• Brinkmann, Gunnar; Degraer, Jan; De Loof, Karel (enero de 2009). "Rehabilitación de un niño no querido: semi-splaying" (PDF) . Software: práctica y experiencia . 39 (1): 33–45. CiteSeerX  10.1.1.84.790 . doi : 10.1002 / spe.v39: 1 . hdl : 11382/102133 .Los resultados muestran que el semi-esparcimiento, que se introdujo en el mismo papel que el esparcimiento, funciona mejor que el esparcimiento en casi todas las condiciones posibles. Esto hace que el semi-esparcimiento sea una buena alternativa para todas las aplicaciones en las que normalmente se aplicaría el esparcimiento. La razón por la que la reproducción se volvió tan prominente mientras que la reproducción parcial es relativamente desconocida y mucho menos estudiada es difícil de entender.

• Cole, Richard; Mishra, Bud; Schmidt, Jeanette; Siegel, Alan (enero de 2000). "Sobre la conjetura de dedo dinámico para árboles de extensión. Parte I: secuencia de n-bloque de registro de clasificación de extensión". Revista SIAM de Computación . 30 (1): 1–43. CiteSeerX  10.1.1.36.4558 . doi : 10.1137 / s0097539797326988 .

• Cole, Richard (enero de 2000). "Sobre la conjetura del dedo dinámico para Splay Trees. Parte II: La prueba". Revista SIAM de Computación . 30 (1): 44–85. CiteSeerX  10.1.1.36.2713 . doi : 10.1137 / S009753979732699X .

• Elmasry, Amr (abril de 2004), "Sobre el teorema de acceso secuencial y la conjetura de Deque para árboles de splay" , Theoretical Computer Science , 314 (3): 459–466, doi : 10.1016 / j.tcs.2004.01.019

• Goodrich, Michael; Tamassia, Roberto; Goldwasser, Michael (2014). Estructuras de datos y algoritmos en Java (6 ed.). Wiley. pag. 506. ISBN 978-1-118-77133-4.

• Knuth, Donald (1997). El arte de la programación informática . 3: Clasificación y búsqueda (3ª ed.). Addison-Wesley. pag. 478. ISBN 0-201-89685-0.

• Lucas, Joan M. (1991). "Sobre la competitividad de los árboles de expansión: relaciones con el problema de búsqueda de unión". Algoritmos en línea: Actas de un taller DIMACS, 11 al 13 de febrero de 1991 . Serie en Matemática Discreta e Informática Teórica. 7 . Centro de Matemática Discreta e Informática Teórica . págs. 95-124. ISBN 0-8218-7111-0.

• Pettie, Seth (2008), "Splay Trees, Davenport-Schinzel Sequences, and the Deque Conjecture" (PDF) , Proc. XIX Simposio ACM-SIAM sobre algoritmos discretos , 0707 : 1115–1124, arXiv : 0707.2160 , Bibcode : 2007arXiv0707.2160P

• Sleator, Daniel D .; Tarjan, Robert E. (1985). "Árboles de búsqueda binarios autoajustables" (PDF) . Revista de la ACM . 32 (3): 652–686. doi : 10.1145 / 3828.3835 . S2CID  1165848 .

• Sundar, Rajamani (1992). "Sobre la conjetura de Deque para el algoritmo de splay". Combinatorica . 12 (1): 95-124. doi : 10.1007 / BF01191208 . S2CID  27422556 .

• Tarjan, Robert E. (1985). "El acceso secuencial en árboles de splay toma un tiempo lineal". Combinatorica . 5 (4): 367–378. doi : 10.1007 / BF02579253 . S2CID  34757821 .

enlaces externos

• Diccionario de algoritmos y estructuras de datos del NIST: Splay Tree
• Implementaciones en C y Java (por Daniel Sleator)
• Punteros para desplegar visualizaciones de árboles
• Implementación rápida y eficiente de árboles Splay
• Implementación de Java Top-Down Splay Tree
• Árboles de cremallera