Tasa de liberación de energía (mecánica de fracturas)

En la mecánica de fractura , la tasa de liberación de energía , es la velocidad a la que la energía se transforma como un material de sufre fractura . Matemáticamente, la tasa de liberación de energía se expresa como la disminución de la energía potencial total por aumento en el área de la superficie de fractura, ^{[1] [2]} y, por lo tanto, se expresa en términos de energía por unidad de área. Se pueden construir varios balances de energía relacionando la energía liberada durante la fractura con la energía de la nueva superficie resultante, así como con otros procesos disipativos como la plasticidad.${\displaystyle G}$y generación de calor. La tasa de liberación de energía es fundamental para el campo de la mecánica de la fractura al resolver problemas y estimar las propiedades del material relacionadas con la fractura y la fatiga .

Definición

Gráfico de carga frente a desplazamiento

La tasa de liberación de energía se define ^[3] como la pérdida instantánea de energía potencial total por unidad de área de crecimiento de grietas ,${\displaystyle G}$${\displaystyle \Pi }$${\displaystyle s}$

${\displaystyle G\equiv -{\frac {\partial \Pi }{\partial s}},}$

donde la energía potencial total se escribe en términos de energía de deformación total , tracción superficial , desplazamiento y fuerza corporal por${\displaystyle \Omega }$${\displaystyle \mathbf {t} }$${\displaystyle \mathbf {u} }$${\displaystyle \mathbf {b} }$

${\displaystyle \Pi =\Omega -\left\{\int _{{\mathcal {S}}_{t}}\mathbf {t} \cdot \mathbf {u} \,dS+\int _{\mathcal {V}}\mathbf {b} \cdot \mathbf {u} \,dV\right\}.}$

La primera integral está sobre la superficie del material y la segunda sobre su volumen .${\displaystyle S_{t}}$${\displaystyle V}$

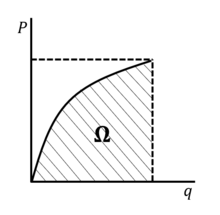
La figura de la derecha muestra el gráfico de una fuerza externa frente al desplazamiento del punto de carga , en el que el área bajo la curva es la energía de deformación. El área blanca entre la curva y el eje - se denomina energía complementaria. En el caso de un material linealmente elástico , es una línea recta y la energía de deformación es igual a la energía complementaria.${\displaystyle P}$${\displaystyle q}$${\displaystyle P}$${\displaystyle P(q)}$

Desplazamiento prescrito

En el caso de desplazamiento prescrito, la energía de deformación se puede expresar en términos del desplazamiento especificado y la superficie de la grieta , y el cambio en esta energía de deformación sólo se ve afectado por el cambio en el área de superficie de la fractura: . En consecuencia, la tasa de liberación de energía en este caso se expresa como ^[3]${\displaystyle \Omega (q,s)}$${\displaystyle \delta \Omega =(\partial \Omega /\partial s)\delta s}$

${\displaystyle G=-\left.{\frac {\partial \Omega }{\partial s}}\right|_{q}.}$

Aquí es donde se puede hacer referencia con precisión a la tasa de liberación de energía de deformación.${\displaystyle G}$

Cargas prescritas

Cuando se prescribe la carga en lugar del desplazamiento, la energía de deformación debe modificarse como . La tasa de liberación de energía se calcula como ^[3]${\displaystyle \Omega (q(P,s),s)}$

${\displaystyle G=-\left.{\frac {\partial }{\partial s}}\right|_{P}\left(\Omega -Pq\right).}$

Si el material es linealmente elástico, entonces se puede escribir${\displaystyle \Omega =Pq/2}$

${\displaystyle G=\left.{\frac {\partial \Omega }{\partial s}}\right|_{P}.}$

G en casos bidimensionales

En los casos de problemas bidimensionales, el cambio en el área de crecimiento de la grieta es simplemente el cambio en la longitud de la grieta multiplicado por el espesor de la muestra. A saber, . Por lo tanto, la ecuación para calcular se puede modificar para el caso 2D: ${\displaystyle \partial s=B\partial a}$${\displaystyle G}$

• Desplazamiento prescrito: ${\displaystyle G=-\left.{\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}\right|_{q}.}$
• Carga prescrita: ${\displaystyle G=-\left.{\frac {1}{B}}{\frac {\partial }{\partial a}}\right|_{P}\left(\Omega -Pq\right).}$
• Carga prescrita, elástico lineal: ${\displaystyle G=\left.{\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}\right|_{P}.}$

Se puede consultar los cálculos de ejemplo incluidos en la siguiente sección para obtener más información. A veces, la energía de deformación se escribe utilizando una energía por unidad de espesor. Esto da${\displaystyle U=\Omega /B}$

• Desplazamiento prescrito: ${\displaystyle G=-\left.{\frac {\partial U}{\partial a}}\right|_{q}.}$
• Carga prescrita: ${\displaystyle G=-\left.{\frac {\partial }{\partial a}}\right|_{P}\left(U-{\frac {Pq}{B}}\right).}$
• Carga prescrita, elástico lineal: ${\displaystyle G=\left.{\frac {\partial U}{\partial a}}\right|_{P}.}$

Relación con los factores de intensidad del estrés

La tasa de liberación de energía está directamente relacionada con el factor de intensidad de la tensión asociado con un modo de carga bidimensional dado ( Modo I, Modo II o Modo III ) cuando la grieta crece en línea recta. ^[3] Esto es aplicable a grietas bajo tensión plana , deformación plana , y de cizallamiento antiplano .

Para el Modo I, la tasa de liberación de energía está relacionada con el factor de intensidad de tensión del Modo I para un material linealmente elástico por${\displaystyle G}$${\displaystyle K_{I}}$

${\displaystyle G={\frac {K_{I}^{2}}{E'}},}$

donde está relacionado con el módulo de Young y la relación de Poisson dependiendo de si el material está bajo tensión plana o deformación plana:${\displaystyle E'}$ ${\displaystyle E}$ ${\displaystyle \nu }$

${\displaystyle E'={\begin{cases}E,&\mathrm {plane~stress} ,\\\\{\dfrac {E}{1-\nu ^{2}}},&\mathrm {plane~strain} .\end{cases}}}$

Para el Modo II, la tasa de liberación de energía se escribe de manera similar como

${\displaystyle G={\frac {K_{II}^{2}}{E'}}.}$

Para el Modo III (cizallamiento antiplano), la tasa de liberación de energía ahora es una función del módulo de cizallamiento ,${\displaystyle \mu }$

${\displaystyle G={\frac {K_{III}^{2}}{2\mu }}.}$

Para una combinación arbitraria de todos los modos de carga, estas soluciones elásticas lineales pueden superponerse como

${\displaystyle G={\frac {K_{I}^{2}}{E'}}+{\frac {K_{II}^{2}}{E'}}+{\frac {K_{III}^{2}}{2\mu }}.}$

Representación alternativa de en términos de [4]${\displaystyle G}$${\displaystyle K}$
${\displaystyle G={\begin{cases}{\frac {(1-\nu )^{2}}{E}}(K_{I}^{2}+K_{II}^{2})+(1-\nu )K_{III}^{2}&{\text{plane strain}}\\{\frac {1}{E}}(K_{I}^{2}+K_{II}^{2})&{\text{plane stress}}\end{cases}}}$ Que puede verse como equivalente a la representación anterior a través de la relación entre el módulo de Young y el módulo de corte: ${\displaystyle E=2G(1+\nu )}$

Relación con la tenacidad a la fractura

El crecimiento de grietas se inicia cuando la tasa de liberación de energía supera un valor crítico , que es una propiedad del material,${\displaystyle G_{c}}$

${\displaystyle G\geq G_{c},}$

Bajo carga Modo-I, la tasa de liberación de energía crítica se relaciona con la tenacidad a la fractura Modo-I , otra propiedad del material, por${\displaystyle G_{c}}$ ${\displaystyle K_{IC}}$

${\displaystyle G_{c}={\frac {K_{IC}^{2}}{E'}}.}$

Calculando G

Hay una variedad de métodos disponibles para calcular la tasa de liberación de energía dadas las propiedades del material, la geometría de la muestra y las condiciones de carga. Algunas dependen de que se cumplan ciertos criterios, como que el material sea completamente elástico o incluso linealmente elástico, y / o que la grieta deba crecer en línea recta. El único método presentado que funciona arbitrariamente es el que utiliza la energía potencial total. Si ambos métodos son aplicables, deberían producir tasas de liberación de energía idénticas.

Energía potencial total

El único método para calcular condiciones arbitrarias es calcular la energía potencial total y diferenciarla con respecto al área de la superficie de la grieta. Por lo general, esto se hace mediante:${\displaystyle G}$

• calcular el campo de tensión resultante de la carga,
• calcular la energía de deformación en el material resultante del campo de tensión,
• calcular el trabajo realizado por las cargas externas,

todo en términos de la superficie de la grieta.

Ejemplo de cálculo del uso de la energía potencial total${\displaystyle G}$

Probeta de doble viga en voladizo (DCB) bajo carga de tracción. Este problema es bidimensional y tiene una carga fija, por lo que con ,${\displaystyle s=aB}$ ${\displaystyle G=-{\frac {1}{B}}\left.{\frac {\partial }{\partial a}}\right|_{P}(\Omega -Pq).}$ Dado que el material es linealmente elástico y , por lo tanto,${\displaystyle \Omega =Pq/2}$ ${\displaystyle G={\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}.}$ Las tensiones en el DCB se deben a las tensiones de flexión en cada viga en voladizo, ${\displaystyle \sigma _{11}(x,y)=-{\frac {M(x)y}{I}}=-{\frac {12Pxy}{Bh^{3}}},}$ donde está la longitud en la página. Usando , uno ahora tiene la energía de tensión${\displaystyle B}$${\displaystyle W=\sigma _{11}^{2}/2E}$ ${\displaystyle \Omega =\int _{V}W\,dV=2B\int _{-h/2}^{h/2}\int _{0}^{a}{\frac {1}{2E}}\left({\frac {12Pxy}{Bh^{3}}}\right)^{2}\,dx\,dy,}$ donde el factor de 2 en el frente se debe a que hay 2 vigas en voladizo. Resolviendo, ${\displaystyle \Omega ={\frac {P^{2}}{B^{3}}}{\frac {4a^{3}}{Eh^{3}}},}$ luego tomando una derivada con respecto a y dividiendo por ,${\displaystyle a}$${\displaystyle B}$ ${\displaystyle G={\frac {P^{2}}{B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.}$

Método de cumplimiento

Si el material es linealmente elástico, el cálculo de su tasa de liberación de energía puede simplificarse mucho. En este caso, la curva de carga frente a desplazamiento del punto de carga es lineal con una pendiente positiva, y el desplazamiento por unidad de fuerza aplicada se define como el cumplimiento, ^[3]${\displaystyle C}$

${\displaystyle C={\frac {q}{P}}.}$

La energía de deformación correspondiente (área bajo la curva) es igual a ^[3]${\displaystyle \Omega }$

${\displaystyle \Omega ={\frac {1}{2}}Pq={\frac {1}{2}}{\frac {q^{2}}{C}}={\frac {1}{2}}P^{2}C.}$

Usando el método de cumplimiento, se puede demostrar que la tasa de liberación de energía para ambos casos de carga prescrita y desplazamiento resulta ser ^[3]

${\displaystyle G={\frac {1}{2}}P^{2}{\frac {\partial C}{\partial s}}.}$

Ejemplo de cálculo de la utilización del método de cumplimiento [3]${\displaystyle G}$

Un espécimen de viga en voladizo doble con espesor B (no se muestra) Considere una muestra de viga en voladizo doble (DCB) como se muestra en la figura de la derecha. El desplazamiento de una sola viga es ${\displaystyle \nu _{max}={\frac {Pa^{3}}{3EI}},\quad {\text{with}}\quad I={\frac {Bh^{3}}{12}}.}$ Por tanto, el desplazamiento del punto de carga resultante es . Sustituya en la ecuación el cumplimiento y simplifique: ${\displaystyle q}$${\displaystyle 2\nu _{max}}$ ${\displaystyle C={\frac {q}{P}}={\frac {8a^{3}}{EBh^{3}}}.}$ Ahora, se calcula como${\displaystyle {\partial C}/{\partial s}}$ ${\displaystyle {\frac {\partial C}{\partial s}}={\frac {\partial C}{\partial a}}{\frac {\partial a}{\partial s}}=\left({\frac {24a^{2}}{EBh^{3}}}\right)\left({\frac {1}{B}}\right).}$ Finalmente, la tasa de liberación de energía de esta muestra de DCB se puede expresar como ${\displaystyle G(P,a)={\frac {1}{2}}P^{2}{\frac {\partial C}{\partial s}}={\frac {P^{2}}{B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.}$ Tenga en cuenta que, alternativamente, la tasa de liberación de energía se puede expresar en términos de y : ${\displaystyle q}$${\displaystyle a}$ ${\displaystyle G(q,a)={\frac {3}{16}}{\frac {Eh^{3}q^{2}}{a^{4}}},}$ indicando que disminuye con la longitud de fisura para el caso de desplazamiento fijo, y viceversa para el caso de carga fija.${\displaystyle G}$${\displaystyle a}$

Múltiples métodos de muestra para materiales no lineales

Ilustración gráfica de G en condiciones de desplazamiento fijo y carga fija

En el caso de un desplazamiento prescrito, manteniendo fija la longitud de la grieta, la tasa de liberación de energía se puede calcular mediante ^[3]

${\displaystyle G=-\int _{0}^{q}{\frac {\partial P}{\partial s}}\,dq,}$

mientras que en el caso de carga prescrita, ^[3]

${\displaystyle G=\int _{0}^{P}{\frac {\partial q}{\partial s}}\,dP.}$

Como se puede ver, en ambos casos, la tasa de liberación de energía multiplicada por el cambio en la superficie devuelve el área entre curvas, lo que indica la energía disipada para la nueva superficie como se ilustra en la figura de la derecha ^[3].${\displaystyle G}$${\displaystyle ds}$

${\displaystyle Gds=-ds\int _{0}^{q}{\frac {\partial P}{\partial s}}\,dq=ds\int _{0}^{P}{\frac {\partial q}{\partial s}}\,dP.}$

Cierre de grietas integral

Dado que la tasa de liberación de energía se define como la derivada negativa de la energía potencial total con respecto al crecimiento de la superficie de la fisura, la tasa de liberación de energía se puede escribir como la diferencia entre la energía potencial antes y después de que la fisura crezca. Después de una derivación cuidadosa, esto nos lleva a la integral de cierre de grietas ^[3]

${\displaystyle G=\lim _{\Delta s\to 0}-{\frac {1}{\Delta s}}\int _{\Delta s}{\frac {1}{2}}\,t_{i}^{0}\left(\Delta u_{i}^{+}-\Delta u_{i}^{-}\right)\,dS,}$

donde está el área de la nueva superficie de fractura, son los componentes de la tracción liberada en la superficie de la fractura superior a medida que crece la grieta, son los componentes del desplazamiento de la abertura de la grieta (la diferencia en los incrementos de desplazamiento entre las superficies superior e inferior de la grieta), y el integral está sobre la superficie del material .${\displaystyle \Delta s}$${\displaystyle t_{i}^{0}}$${\displaystyle \Delta u_{i}^{+}-\Delta u_{i}^{-}}$${\displaystyle S}$

La integral de cierre de grietas es válida solo para materiales elásticos, pero sigue siendo válida para grietas que crecen en cualquier dirección. Sin embargo, para una grieta bidimensional que de hecho crece en línea recta, la integral de cierre de la grieta se simplifica a ^[3]

${\displaystyle G=\lim _{\Delta a\to 0}{\frac {1}{\Delta a}}\int _{0}^{\Delta a}\sigma _{i2}(x_{1},0)u_{i}(\Delta a-x_{1},\pi )\,dx_{1},}$

donde es la nueva longitud de la grieta y los componentes de desplazamiento se escriben en función de las coordenadas polares y .${\displaystyle \Delta a}$${\displaystyle r=\Delta a-x_{1}}$${\displaystyle \theta =\pi }$

Ejemplo de cálculo del uso de la integral de cierre de fisuras${\displaystyle G}$

Probeta de doble viga en voladizo (DCB) bajo carga de tracción. Considere la grieta en la muestra de DCB que se muestra en la figura. Los componentes de esfuerzo y desplazamiento distintos de cero vienen dados por [3] como ${\displaystyle \sigma _{22}(x_{1},0)={\frac {K_{I}}{\sqrt {2\pi x_{1}}}},\qquad u_{22}(\Delta a-x_{1},\pi )={\frac {8K_{I}}{E}}{\sqrt {\frac {\Delta a_{1}-x_{1}}{2\pi }}}.}$ La integral de cierre de la grieta para este material linealmente elástico, asumiendo que la grieta crece en línea recta, es ${\displaystyle G={\frac {2K_{I}^{2}}{\pi E}}\,\lim _{\Delta a\to 0}{\frac {1}{\Delta a}}\int _{0}^{\Delta a}{\sqrt {\frac {\Delta a_{1}-x_{1}}{x_{1}}}}\,dx_{1}.}$ Considere reescalar la integral usando para${\displaystyle \xi =x_{1}/\Delta a}$ ${\displaystyle G={\frac {2K_{I}^{2}}{\pi E}}\int _{0}^{1}{\sqrt {\frac {1-\xi }{\xi }}}\,d\xi ,}$ donde se calcula que la integral más simple es ${\displaystyle \int _{0}^{1}{\sqrt {\frac {1-\xi }{\xi }}}\,d\xi ={\frac {\pi }{2}},}$ dejando la tasa de liberación de energía como ${\displaystyle G={\frac {K_{I}^{2}}{E}},}$ la relación esperada. En este caso, no es sencillo obtener directamente de la carga y la geometría del problema, pero dado que la grieta crece en línea recta y el material es linealmente elástico, la tasa de liberación de energía aquí debería ser la misma que la tasa de liberación de energía calculada usando los otros métodos. Esto permite recuperar indirectamente el factor de intensidad del estrés para este problema como${\displaystyle K_{I}}$ ${\displaystyle K_{I}={\frac {P}{B}}{\frac {2a}{h}}{\sqrt {\frac {3}{h}}}.}$

J - integral

En ciertas situaciones, la tasa de liberación de energía se puede calcular usando la integral J , es decir , usando ^[3]${\displaystyle G}$${\displaystyle G=J}$

${\displaystyle J=\int _{\Gamma }\left(Wn_{1}-t_{i}\,{\frac {\partial u_{i}}{\partial x_{1}}}\right)\,d\Gamma ,}$

donde es la densidad de energía de deformación elástica, es el componente del vector unitario normal a , la curva utilizada para la integral de línea, son los componentes del vector de tracción , donde es el tensor de tensión y son los componentes del vector de desplazamiento.${\displaystyle W}$${\displaystyle n_{1}}$${\displaystyle x_{1}}$${\displaystyle \Gamma }$${\displaystyle t_{i}}$${\displaystyle \mathbf {t} ={\boldsymbol {\sigma }}\cdot \mathbf {n} }$${\displaystyle {\boldsymbol {\sigma }}}$${\displaystyle u_{i}}$

Esta integral es cero sobre una ruta simple cerrada y es independiente de la ruta , lo que permite que se utilice para calcular cualquier ruta simple que comience y termine en las caras de la grieta . Para equiparar la tasa de liberación de energía a la integral J, se deben cumplir las siguientes condiciones:${\displaystyle J}$${\displaystyle G=J}$

• la grieta debe estar creciendo en línea recta, y
• la deformación cerca de la grieta (encerrada por ) debe ser elástica (no plástica).${\displaystyle \Gamma }$

La integral J puede calcularse con estas condiciones violadas, pero entonces . Cuando no se violan, se puede relacionar la tasa de liberación de energía y la integral J con los módulos elásticos y los factores de intensidad de la tensión utilizando ^[3]${\displaystyle G\neq J}$

${\displaystyle G=J={\frac {K_{I}^{2}}{E'}}+{\frac {K_{II}^{2}}{E'}}+{\frac {K_{III}^{2}}{2\mu }}.}$

Ejemplo de cálculo del uso de la integral J [3]${\displaystyle G}$

Probeta de doble viga en voladizo (DCB) bajo carga de tracción. Trayectoria integral J para la muestra DCB bajo carga de tracción. Considere la muestra de viga en voladizo doble que se muestra en la figura, donde la grieta centrada en la viga de altura tiene una longitud de , y se aplica una carga para abrir la grieta. Suponga que el material es linealmente elástico y que la grieta crece hacia adelante. Considere un camino rectangular que se muestra en la segunda figura: comience en la cara superior de la grieta, (1) suba hasta la parte superior en , (2) vaya a la derecha más allá de la punta de la grieta, (3) baje hasta la parte inferior en , ( 4) vaya por la parte inferior hacia la izquierda y (5) vuelva a subir hasta la cara inferior de la grieta. La integral J es cero a lo largo de muchas partes de este camino. El material se descarga efectivamente detrás de la grieta, por lo que tanto la densidad de energía de deformación como la tracción son cero a lo largo de (1) y (5) y, por lo tanto, la integral J. A lo largo de (2) y (4) uno tiene${\displaystyle 2h}$${\displaystyle a}$${\displaystyle P}$${\displaystyle h}$${\displaystyle -2h}$${\displaystyle n_{1}=0}$así como (sin tracción en la superficie libre), por lo que la integral J es cero en (2) y (4) también. Esto deja solo (3); asumiendo que uno está lo suficientemente lejos de la grieta en (3), el término de tracción es cero ya que y lejos de la grieta, dejando${\displaystyle \mathbf {t} =\mathbf {0} }$${\displaystyle u_{1}=0}$${\displaystyle \sigma _{12}=0}$ ${\displaystyle J=\int _{\Gamma _{3}}Wn_{1}\,d\Gamma _{3}.}$ ${\displaystyle n_{1}=1}$a lo largo de (3), y se debe al esfuerzo de flexión de una viga en voladizo${\displaystyle W}$ ${\displaystyle \sigma _{11}(y)=-{\frac {My}{I}}=-{\frac {12Pay}{Bh^{3}}},}$ donde está la longitud en la página. Usando , uno ahora tiene${\displaystyle B}$${\displaystyle W=\sigma _{11}^{2}/2E}$ ${\displaystyle J=2\int _{-h/2}^{h/2}{\frac {1}{2E}}\left({\frac {12Pay}{Bh^{3}}}\right)^{2}\,dy,}$ donde el factor de 2 en el frente se debe a que hay 2 vigas en voladizo. Resolviendo, ${\displaystyle G=J={\frac {P^{2}}{B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.}$

Métodos computacionales en mecánica de fracturas.

Existen varios métodos para calcular con elementos finitos. Aunque es posible un cálculo directo de la integral J (utilizando las deformaciones y tensiones generadas por FEA ), existen enfoques aproximados para algún tipo de crecimiento de grietas y proporcionan una precisión razonable con cálculos sencillos. Esta sección desarrollará algunos métodos relativamente simples para el análisis de fracturas utilizando simulaciones numéricas.${\displaystyle G}$

Método de liberación nodal

Si la grieta crece recta, la tasa de liberación de energía se puede descomponer como una suma de 3 términos asociados con la energía en cada 3 modos. Como resultado, el método de liberación nodal (NR) se puede utilizar para determinar a partir de los resultados de FEA. La tasa de liberación de energía se calcula en los nodos de la malla de elementos finitos para la grieta en una longitud inicial y se extiende una pequeña distancia . Primero, calculamos la variación de desplazamiento en el nodo de interés (antes y después de que se suelte el nodo de la punta de la grieta). En segundo lugar, realizamos un seguimiento de la fuerza nodal producida por FEA. Finalmente, podemos encontrar cada uno de los componentes usando las siguientes fórmulas:${\displaystyle G_{i}}$${\displaystyle G_{i}}$${\displaystyle \Delta a}$${\displaystyle \Delta {\vec {u}}={\vec {u}}^{(t+1)}-{\vec {u}}^{(t)}}$${\displaystyle {\vec {F}}}$${\displaystyle G}$

Figura 1: Desbordamiento de grietas entre dos pasos de tiempo consecutivos usando liberación nodal (NR)

$${\displaystyle G_{1}^{\text{NR}}={\frac {1}{\Delta a}}F_{2}{\frac {\Delta u_{2}}{2}}}$$

$${\displaystyle G_{2}^{\text{NR}}={\frac {1}{\Delta a}}F_{1}{\frac {\Delta u_{1}}{2}}}$$

$${\displaystyle G_{3}^{\text{NR}}={\frac {1}{\Delta a}}F_{3}{\frac {\Delta u_{3}}{2}}}$$

¿Dónde está el ancho del elemento que delimita la punta de la grieta? La precisión del método depende en gran medida del refinamiento de la malla, tanto porque el desplazamiento y las fuerzas dependen de él, como porque . Tenga en cuenta que las ecuaciones anteriores se derivan utilizando la integral de cierre de fisuras.${\displaystyle \Delta a}$${\displaystyle G=\lim _{\Delta a\to 0}G^{\text{NR}}}$

Si la tasa de liberación de energía excede un valor crítico, la grieta crecerá. En este caso, se realiza una nueva simulación FEA (para el siguiente paso de tiempo) donde se libera el nodo en la punta de la grieta. Para un sustrato delimitado, simplemente podemos dejar de aplicar condiciones de límite de Dirichlet fijas en el nodo de la punta de la grieta del paso de tiempo anterior (es decir, los desplazamientos ya no están restringidos). Para una fisura simétrica, necesitaríamos actualizar la geometría del dominio con una abertura de fisura más larga (y por lo tanto generar una nueva malla ^[5] ).

Cierre de grietas modificado integral

Similar al método de liberación nodal, la integral de cierre de grietas modificada (MCCI) es un método para calcular la tasa de liberación de energía utilizando los desplazamientos y fuerzas nodales FEA . ^{[6] [7]} Donde representa la dirección correspondiente a los vectores base cartesianos con origen en la punta de la grieta y representa el índice nodal. MCCI es más eficiente computacionalmente que el método de liberación nodal porque solo requiere un análisis por cada incremento de crecimiento de grietas.${\displaystyle (u_{i}^{j})}$${\displaystyle (F_{i}^{j})}$${\displaystyle i}$${\displaystyle j}$

Una condición necesaria para el método MCCI es la longitud uniforme del elemento a lo largo de la cara de la grieta en la dirección. Además, este método requiere una discretización suficiente de modo que en la longitud de un elemento los campos de tensión sean auto-similares . Esto implica que a medida que se propaga la grieta. A continuación se muestran ejemplos del método MCCI con dos tipos de elementos finitos comunes.${\displaystyle (\Delta a)}$${\displaystyle x_{1}-}$${\displaystyle K(a+\Delta a)\approx K(a)}$

Elementos de 4 nodos

Figura 2: Esquema del proceso MCCI para elementos rectangulares lineales de 4 nodos.

Los elementos lineales cuadrados de 4 nodos que se ven en la Figura 2 tienen una distancia entre nodos e igual a Considere una grieta con su punta ubicada en el nodo Similar al método de liberación nodal, si la grieta se propagara la longitud de un elemento a lo largo de la línea de simetría ( paralelo al eje-) el desplazamiento de la abertura de la grieta sería el desplazamiento en la punta de la grieta anterior, es decir, y la fuerza en la nueva punta de la grieta sería Dado que se supone que el crecimiento de la grieta es auto-similar, el desplazamiento en el nodo después de que la grieta se propaga es igual al desplazamiento en el nodo antes de que se propague la grieta. Este mismo concepto se puede aplicar a las fuerzas en el nodo y${\displaystyle j}$${\displaystyle j+1}$${\displaystyle \Delta a.}$${\displaystyle j.}$${\displaystyle x_{1}}$${\displaystyle {\boldsymbol {u^{j}}}}$${\displaystyle (j+1)}$${\displaystyle {\boldsymbol {F}}^{j+1}.}$${\displaystyle j}$${\displaystyle j-1}$${\displaystyle j+1}$${\displaystyle j.}$ Utilizando el mismo método que se muestra en la sección de liberación nodal, recuperamos las siguientes ecuaciones para la tasa de liberación de energía:

${\displaystyle G_{1}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{2}^{j}{\Delta u_{2}^{j-1}}}$

${\displaystyle G_{2}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{1}^{j}{\Delta u_{1}^{j-1}}}$

${\displaystyle G_{3}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{3}^{j}{\Delta u_{3}^{j-1}}}$

Dónde (desplazamiento por encima y por debajo de la cara de la grieta, respectivamente). Debido a que tenemos una línea de simetría paralela a la grieta, podemos suponer${\displaystyle \Delta u_{i}^{j-1}=u_{i}^{(+)j-1}-u_{i}^{(-)j-1}}$${\displaystyle u_{i}^{(+)j-1}=-u_{i}^{(-)j-1}.}$

Por lo tanto, ${\displaystyle \Delta u_{i}^{j-1}=2u_{i}^{(+)j-1}.}$

Elementos de 8 nodos

Figura 3: Esquema del proceso MCCI para elementos rectangulares cuadráticos de 9 nodos.

Los elementos rectangulares de 8 nodos que se ven en la Figura 3 tienen funciones de base cuadrática . El proceso para calcular G es el mismo que el de los elementos de 4 nodos con la excepción de que (el crecimiento de la grieta sobre un elemento) es ahora la distancia desde el nodo hasta una vez más, asumiendo que el crecimiento de la grieta recta auto-similar es la tasa de liberación de energía se puede calcular utilizando las siguientes ecuaciones:${\displaystyle \Delta a}$${\displaystyle j}$${\displaystyle j+2.}$

${\displaystyle G_{1}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{2}^{j}{\Delta u_{2}^{j-2}}+F_{2}^{j+1}{\Delta u_{2}^{j-1}}\right)}$

${\displaystyle G_{2}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{1}^{j}{\Delta u_{1}^{j-2}}+F_{1}^{j+1}{\Delta u_{1}^{j-1}}\right)}$

${\displaystyle G_{3}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{3}^{j}{\Delta u_{3}^{j-2}}+F_{3}^{j+1}{\Delta u_{3}^{j-1}}\right)}$

Al igual que con el método de liberación nodal, la precisión de MCCI depende en gran medida del nivel de discretización a lo largo de la punta de la grieta, es decir, la precisión también depende de la elección del elemento. Una malla de elementos cuadráticos de 8 nodos puede producir resultados más precisos que una malla de elementos lineales de 4 nodos con el mismo número de grados de libertad ^[8] en la malla.${\displaystyle G=\lim _{\Delta a\to 0}G^{\text{MCCI}}.}$

Enfoque integral de dominio para J

Figura 4: Integral de dominio de contorno para la integral J

La integral J se puede calcular directamente usando las funciones de malla y forma de elementos finitos. ^[9] consideramos un countour dominio como se muestra en la figura 4 y seleccione una función suave arbitraria de tal manera que en y sobre .${\displaystyle {\tilde {q}}(x_{1},x_{2})=\sum _{i}N_{i}(x_{1},x_{2}){\tilde {q}}_{i}}$${\displaystyle {\tilde {q}}=1}$${\displaystyle \Gamma }$${\displaystyle {\tilde {q}}=0}$${\displaystyle {\mathcal {C}}_{1}}$

Para grietas elásticos lineales creciente hacia el frente, . La tasa de liberación de energía se puede calcular sobre el área delimitada por el contorno utilizando una formulación actualizada:${\displaystyle G=J}$${\displaystyle J=\int _{\mathcal {A}}(\sigma _{ij}u_{i,1}{\tilde {q}}_{,j}-W{\tilde {q}}_{,1})d{\mathcal {A}}}$

La fórmula anterior se puede aplicar a cualquier área anular que rodee la punta de la grieta (en particular, se puede usar un conjunto de elementos vecinos). Este método es muy preciso, incluso con una malla gruesa alrededor de la punta de la grieta (se puede elegir un dominio de integración ubicado lejos, con tensiones y desplazamientos menos sensibles al refinamiento de la malla).

Derivación de la integral J para el enfoque integral de dominio

El J-intregral se puede expresar en todo el contorno de la siguiente manera: ${\displaystyle G=J=\int _{\Gamma }(Wn_{1}-t_{i}{\frac {\partial u_{i}}{\partial x_{1}}})d\Gamma =\int _{{\mathcal {C}}_{1}+{\mathcal {C}}_{+}+{\mathcal {C}}_{-}-{\mathcal {C}}}(Wn_{1}-\sigma _{ij}n_{j}{\frac {\partial u_{i}}{\partial x_{1}}}){\tilde {q}}d\Gamma }$ Con . , En y el trabajo y las tensiones se anulan en y , por lo tanto, mediante la aplicación de la divergencia teorema esto conduce a:${\displaystyle {\mathcal {C}}={\mathcal {C}}_{1}+{\mathcal {C}}_{+}+{\mathcal {C}}_{-}-\Gamma }$${\displaystyle {\vec {n}}=-{\vec {m}}}$${\displaystyle {\tilde {q}}=0}$${\displaystyle {\mathcal {C}}_{1}}$${\displaystyle {\mathcal {C}}_{+}}$${\displaystyle {\mathcal {C}}_{-}}$ ${\displaystyle J=\int _{\mathcal {C}}(-Wm_{1}+\sigma _{ij}m_{i}{\frac {\partial u_{i}}{\partial x_{1}}})d{\mathcal {C}}=\int _{\mathcal {A}}({\frac {\partial \sigma _{ij}u_{i,1}{\tilde {q}}}{\partial x_{j}}}-{\frac {\partial W{\tilde {q}}}{\partial x_{1}}})d{\mathcal {A}}}$ Finalmente, notando eso y usando la ecuación de equilibrio:${\displaystyle {\frac {\partial W}{\partial x_{1}}}=\sigma _{ij}{\frac {\partial ^{2}u_{i}}{\partial x_{j}\partial x_{1}}}}$ ${\displaystyle J=\int _{\mathcal {A}}(\sigma _{ij}u_{i,1}{\tilde {q}}_{,j}-W{\tilde {q}}_{,1})d{\mathcal {A}}}$

Elementos singulares de punta de grieta 2-D

Los métodos antes mencionados para calcular la tasa de liberación de energía se acercan asintóticamente a la solución real con una mayor discretización, pero no logran capturar completamente la singularidad de la punta de la grieta. Se pueden realizar simulaciones más precisas utilizando elementos de un cuarto de punto alrededor de la punta de la grieta. ^[10] Estos elementos tienen una singularidad incorporada que produce con mayor precisión campos de tensión alrededor de la punta de la grieta. La ventaja del método de un cuarto de punto es que permite mallas de elementos finitos más gruesas y reduce en gran medida el costo computacional. Además, estos elementos se derivan de pequeñas modificaciones a elementos finitos comunes sin requerir programas computacionales especiales para su análisis. Para los propósitos de esta sección, se examinarán los materiales elásticos, aunque este método puede extenderse a los materiales elásticos.mecánica de fracturas plásticas . ^{[11] [12] [13] [14]} Suponiendo una elasticidad perfecta, los campos de tensión experimentarán una singularidad en la punta de la grieta.${\displaystyle {\frac {1}{\sqrt {r}}}}$

Elemento isoparamétrico de 8 nodos

Figura 5: Elemento mapeado y principal del elemento finito isoparamétrico de 8 nodos. Tenga en cuenta la ubicación de un cuarto de punto de los nodos en el elemento mapeado.

El elemento cuadrática 8-nodo se describen en la Figura 5 tanto en el espacio de los padres con coordenadas locales y y por el elemento de mapeado en el espacio físico / global por y del elemento padre está asignada desde el espacio local para el espacio físico por las funciones de forma y la Coordenadas del grado de libertad La punta de la grieta se encuentra en o ${\displaystyle \xi }$${\displaystyle \eta ,}$${\displaystyle x}$${\displaystyle y.}$${\displaystyle N_{i}(\xi ,\eta )}$${\displaystyle (x_{i},y_{i}).}$${\displaystyle \xi =-1,\eta =-1}$${\displaystyle x=0,y=0.}$

${\displaystyle x(\xi ,\eta )=\sum _{i=1}^{8}N_{i}(\xi ,\eta )x_{i}}$

${\displaystyle y(\xi ,\eta )=\sum _{i=1}^{8}N_{i}(\xi ,\eta )y_{i}}$

De manera similar, los desplazamientos (definidos como ) también se pueden mapear.${\displaystyle u\equiv u_{1},v\equiv u_{2}}$

${\displaystyle u(\xi ,\eta )=\sum _{i=1}^{8}N_{i}(\xi ,\eta )u_{i}}$

${\displaystyle v(\xi ,\eta )=\sum _{i=1}^{8}N_{i}(\xi ,\eta )v_{i}}$

Una propiedad de las funciones de forma en el método de elementos finitos es el soporte compacto , específicamente la propiedad delta de Kronecker (es decir, en el nodo y cero en todos los demás nodos). Esto da como resultado las siguientes funciones de forma para los elementos cuadráticos de 8 nodos: ^[8]${\displaystyle N_{i}=1}$${\displaystyle i}$

${\displaystyle N_{1}={\frac {-(\xi -1)(\eta -1)(1+\eta +\xi )}{4}}}$

${\displaystyle N_{2}={\frac {(\xi +1)(\eta -1)(1+\eta -\xi )}{4}}}$

${\displaystyle N_{3}={\frac {(\xi +1)(\eta +1)(-1+\eta +\xi )}{4}}}$

${\displaystyle N_{4}={\frac {-(\xi -1)(\eta +1)(-1+\eta -\xi )}{4}}}$

${\displaystyle N_{5}={\frac {(1-\xi ^{2})(1-\eta )}{2}}}$

${\displaystyle N_{6}={\frac {(1+\xi )(1-\eta ^{2})}{2}}}$

${\displaystyle N_{7}={\frac {(1-\xi ^{2})(1+\eta )}{2}}}$

${\displaystyle N_{8}={\frac {(1-\xi )(1-\eta ^{2})}{2}}}$

Cuando se considera una línea frente a la grieta que es colineal con el eje - (es decir ), todas las funciones básicas son cero excepto por${\displaystyle x}$${\displaystyle N_{i}(\xi ,\eta =-1)}$${\displaystyle N_{1,2,5}.}$

${\displaystyle N_{1}(\xi ,-1)=-{\frac {\xi (1-\xi )}{2}}}$

${\displaystyle N_{2}(\xi ,-1)={\frac {\xi (1+\xi )}{2}}}$

${\displaystyle N_{5}(\xi ,-1)=(1-\xi ^{2})}$

Calcular la deformación normal implica usar la regla de la cadena para tomar la derivada del desplazamiento con respecto a${\displaystyle x.}$

${\displaystyle \gamma _{xx}={\frac {\partial u}{\partial x}}=\sum _{i=1,2,5}{\frac {\partial N_{i}}{\partial \xi }}{\frac {\partial \xi }{\partial x}}u_{i}}$

Figura 6: Elemento triangular mapeado a partir de un elemento rectangular de 8 nodos.

Si los nodos están espaciados uniformemente en el elemento rectangular, la deformación no contendrá la singularidad. Al mover los nodos 5 y 8 a una cuarta parte de la longitud del elemento más cerca de la punta de la grieta como se ve en la figura 5, el mapeo de se convierte en:${\displaystyle ({\tfrac {L}{4}})}$${\displaystyle \xi \rightarrow x}$

${\displaystyle x(\xi )={\frac {\xi (1+\xi )}{2}}L+(1-\xi ^{2}){\frac {L}{4}}}$

Resolver y tomar la derivada da como resultado:${\displaystyle \xi }$

${\displaystyle \xi (x)=-1+2{\sqrt {\frac {x}{L}}}}$

${\displaystyle {\frac {\partial \xi }{\partial x}}={\frac {1}{\sqrt {xL}}}}$

Conectando este resultado a la ecuación de deformación se obtiene el resultado final:

${\displaystyle \gamma _{xx}={\frac {4}{L}}\left({\frac {u_{2}}{2}}-u_{5}\right)+{\frac {1}{\sqrt {xL}}}\left(2u_{5}-{\frac {u_{2}}{5}}\right)}$

Al mover los nodos medios a una posición de un cuarto, se obtiene la singularidad correcta de la punta de la grieta.${\displaystyle {\frac {1}{\sqrt {r}}}}$

Otros tipos de elementos

Figura 7: Elemento de triángulo natural

El método del elemento rectangular no permite que los elementos singulares se enreden fácilmente alrededor de la punta de la grieta. Esto impide la capacidad de capturar la dependencia angular de los campos de tensión que es fundamental para determinar la trayectoria de la fisura. Además, excepto a lo largo de los bordes del elemento, la singularidad existe en una región muy pequeña cerca de la punta de la grieta. La Figura 6 muestra otro método de un cuarto de punto para modelar esta singularidad. El elemento rectangular de 8 nodos se puede mapear en un triángulo. ^[15] Esto se hace colapsando los nodos en la línea a la ubicación del nodo medio y moviendo los nodos medios en${\displaystyle {\frac {1}{\sqrt {r}}}}$${\displaystyle \xi =-1}$${\displaystyle \eta =\pm 1}$a la ubicación de un cuarto de punto. El rectángulo colapsado puede rodear más fácilmente la punta de la grieta, pero requiere que los bordes del elemento sean rectos o se reducirá la precisión del cálculo del factor de intensidad de la tensión.

Un mejor candidato para el método de un cuarto de punto es el triángulo natural como se ve en la Figura 7. La geometría del elemento permite rodear fácilmente la punta de la grieta y simplificar el mallado. Siguiendo el mismo procedimiento descrito anteriormente, el campo de desplazamiento y deformación de los elementos triangulares son:

${\displaystyle u=u_{3}+{\sqrt {\frac {x}{L}}}\left[4u_{6}-3u_{3}-u_{1}\right]+{\frac {x}{L}}\left[2u_{1}+2u_{3}-4u_{6}\right]}$

${\displaystyle \gamma _{xx}={\frac {\partial u}{\partial x}}={\frac {1}{\sqrt {xL}}}\left[-{\frac {u_{1}}{2}}-{\frac {3u_{3}}{2}}+2u_{6}\right]+{\frac {1}{L}}\left[2u_{1}+2u_{3}-4u_{6}\right]}$

Este método reproduce los dos primeros términos de las soluciones de Williams ^[16] con un término constante y singular.

Una ventaja del método de un cuarto de punto es que se puede generalizar fácilmente a modelos tridimensionales. Esto puede reducir en gran medida el cálculo en comparación con otros métodos tridimensionales, pero puede provocar errores si la punta de la grieta se propaga con un gran grado de curvatura. ^[17]

Ver también

• Mecánica de fracturas
• Factor de intensidad de estrés
• Tenacidad a la fractura
• J-integral

Referencias

1. Li, FZ; Shih, CF; Needleman, A. (1985). "Una comparación de métodos para calcular las tasas de liberación de energía". Ingeniería Mecánica de Fracturas . 21 (2): 405–421. doi : 10.1016 / 0013-7944 (85) 90029-3 . ISSN  0013-7944 .
2. Arroz, JR; Budiansky, B. (1973). "Leyes de conservación y tasas de liberación de energía". Revista de Mecánica Aplicada . 40 (1): 201–3. Código bibliográfico : 1973JAM .... 40..201B . doi : 10.1115 / 1.3422926 . S2CID 13910502 . 
3. Alan Zehnder (2012). Mecánica de fracturas . Londres; Nueva York: Springer Science + Business Media. ISBN 9789400725942.
4. Soboyejo, WO (2003). "11.6.5 Equivalencia de G y K". Propiedades mecánicas de los materiales de ingeniería. Marcel Dekker. ISBN 0-8247-8900-8 . OCLC 300921090. 
5. Tradegard, A. (15 de julio de 1998). "Técnica de remallado FEM aplicada a problemas de crecimiento de grietas". Métodos informáticos en mecánica e ingeniería aplicadas . 160 (1-2): 115-131. Código bibliográfico : 1998CMAME.160..115T . doi : 10.1016 / s0045-7825 (97) 00287-9 .
6. Rybicki, EF; Kanninen, MF (enero de 1977). "Un cálculo de elementos finitos de los factores de intensidad de la tensión mediante una integral de cierre de fisura modificada". Ingeniería Mecánica de Fracturas . 9 (4): 931–938. doi : 10.1016 / 0013-7944 (77) 90013-3 . ISSN 0013-7944 . 
7. Sethuraman, R .; Maiti, SK (enero de 1988). "Cálculo basado en elementos finitos de la tasa de liberación de energía de deformación por integral de cierre de fisura modificado". Ingeniería Mecánica de Fracturas . 30 (2): 227–231. doi : 10.1016 / 0013-7944 (88) 90226-3 . ISSN 0013-7944 . 
8. Zehnder, Alan T. (3 de enero de 2012). Mecánica de fracturas . Dordrecht. ISBN 9789400725959. OCLC  773034407 .
9. Zehnder, Alan T. (2012). Mecánica de fracturas . Apuntes de clases en Mecánica Aplicada y Computacional. 62 . Dordrecht: Springer Holanda. doi : 10.1007 / 978-94-007-2595-9 . ISBN 9789400725942.
10. Henshell, RD; Shaw, KG (1975). "Los elementos finitos de la punta de la grieta son innecesarios". Revista Internacional de Métodos Numéricos en Ingeniería . 9 (3): 495–507. Código bibliográfico : 1975IJNME ... 9..495H . doi : 10.1002 / nme.1620090302 . ISSN 0029-5981 . 
11. Barsoum, Roshdy S. (1977). "Elementos triangulares de cuarto de punto como elementos de punta de fisura elásticos y perfectamente plásticos". Revista Internacional de Métodos Numéricos en Ingeniería . 11 (1): 85–98. Código bibliográfico : 1977IJNME..11 ... 85B . doi : 10.1002 / nme.1620110109 . ISSN 0029-5981 . 
12. Sol, CT; Jin, Z.-H. (2012), "Criterios de fractura elástica-plástica", Fracture Mechanics , Elsevier, págs. 171–187, doi : 10.1016 / b978-0-12-385001-0.00007-9 , ISBN 9780123850010
13. Stern, Morris (1979). "Familias de elementos conformes consistentes con campos derivados singulares". Revista Internacional de Métodos Numéricos en Ingeniería . 14 (3): 409–421. Código Bibliográfico : 1979IJNME..14..409S . doi : 10.1002 / nme.1620140307 . ISSN 0029-5981 . 
14. Levy, N .; Marcal, PV; Ostergren, WJ; Rice, JR (junio de 1971). "Producción a pequeña escala cerca de una grieta en la deformación plana: un análisis de elementos finitos". Revista Internacional de Mecánica de Fracturas . 7 (2). doi : 10.1007 / bf00183802 . ISSN 0020-7268 . 
15. Barsoum, Roshdy S. (1976). "Sobre el uso de elementos finitos isoparamétricos en mecánica de fracturas lineales". Revista Internacional de Métodos Numéricos en Ingeniería . 10 (1): 25–37. Código bibliográfico : 1976IJNME..10 ... 25B . doi : 10.1002 / nme.1620100103 . ISSN 0029-5981 . 
16. Williams, ML (1959). "Las tensiones en torno a una falla o fisura en medios disímiles" . Boletín de la Sociedad Sismológica de América . 49 : 199-204.
17. Peano, A .; Pasini, A. (febrero de 1982). "Una advertencia contra el mal uso de elementos de un cuarto de punto". Revista Internacional de Métodos Numéricos en Ingeniería . 18 (2): 314–320. Código bibliográfico : 1982IJNME..18..314P . doi : 10.1002 / nme.1620180212 . ISSN 0029-5981 . 

enlaces externos

• Notas de mecánica de fracturas no lineales por el profesor John Hutchinson (de la Universidad de Harvard)
• Tasa de liberación de energía de deformación de Griffith en www.fracturemechanics.org