Bloquear autómata celular

La vecindad de Margolus para un autómata celular de bloques bidimensionales. La partición de las celdas alterna entre el conjunto de bloques de 2 × 2 indicado por las líneas azules sólidas y el conjunto de bloques indicado por las líneas rojas discontinuas.

Un autómata celular de bloque o un autómata celular de partición es un tipo especial de autómata celular en el que la celosía de las células se divide en bloques no superpuestos (con diferentes particiones en diferentes pasos de tiempo) y la regla de transición se aplica a un bloque completo a la vez. en lugar de una sola celda. Los autómatas celulares de bloque son útiles para simulaciones de cantidades físicas, porque es sencillo elegir reglas de transición que obedezcan restricciones físicas como las leyes de reversibilidad y conservación . ^[1]

Definición

Un autómata celular de bloque consta de los siguientes componentes: ^{[1] [2]}

• Una celosía regular de células.
• Un conjunto finito de los estados en los que cada celda puede estar
• Una partición de las celdas en una teselación uniforme en la que cada mosaico de la partición tiene el mismo tamaño y forma.
• Una regla para cambiar la partición después de cada paso de tiempo
• Una regla de transición, una función que toma como entrada una asignación de estados para las celdas en un solo mosaico y produce como salida otra asignación de estados para las mismas celdas.

En cada paso de tiempo, la regla de transición se aplica de forma simultánea y sincrónica a todos los mosaicos de la partición. Luego, la partición se desplaza y la misma operación se repite en el siguiente paso de tiempo, y así sucesivamente. De esta manera, como con cualquier autómata celular, el patrón de estados de celda cambia con el tiempo para realizar algún cálculo o simulación no trivial.

Barrios

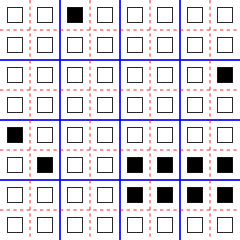
El esquema de partición más simple es probablemente el barrio de Margolus , que lleva el nombre de Norman Margolus , quien estudió por primera vez los autómatas celulares de bloques utilizando esta estructura de barrio. En el barrio de Margolus, la celosía se divide en bloques de 2 celdas (o cuadrados de 2 × 2 en dos dimensiones, o cubos de 2 × 2 × 2 en tres dimensiones, etc.) que se desplazan una celda (a lo largo de cada dimensión) en Pasos de tiempo alternativos. ^{[1] [2] [3]}

Una técnica estrechamente relacionada debida a K. Morita y M. Harao ^[4] consiste en dividir cada celda en un número finito de partes, cada parte dedicada a algún vecino. La evolución procede intercambiando las partes correspondientes entre vecinos y luego aplicando en cada celda una transformación puramente local que depende solo del estado de la celda (y no de los estados de sus vecinas). Con tal esquema de construcción, se garantiza que el autómata celular sea reversible si la transformación local es en sí misma una biyección.${\displaystyle F}$${\displaystyle F}$. Esta técnica puede verse como un autómata celular en bloque sobre un entramado de células más fino, formado por las partes de cada célula más grande; los bloques de esta celosía más fina alternan entre los conjuntos de partes dentro de una sola celda grande y los conjuntos de partes en celdas vecinas que comparten partes entre sí.

Reversibilidad y conservación

Siempre que la regla para la evolución de cada bloque sea reversible , el autómata completo también lo será. Más fuertemente, en este caso, el comportamiento inverso en el tiempo del autómata también se puede describir como un autómata celular de bloque, con la misma estructura de bloque y con una regla de transición que invierte la regla del autómata original dentro de cada bloque. Lo contrario también es cierto: si los bloques no son reversibles individualmente, la evolución global no puede ser reversible: si dos configuraciones diferentes x y y de una ventaja de bloque al mismo estado resultado z , a continuación, una configuración global con x en un bloque serían indistinguible después de un paso de la configuración en la que la x se reemplaza pory . Es decir, un autómata celular es reversible globalmente si y solo si es reversible a nivel de bloque. ^[5]

La facilidad de diseño de bloque reversible autómatas celulares, y de probar bloque autómatas celulares para la reversibilidad, es en fuerte contraste con los autómatas celulares con otras estructuras de la vecindad no de bloque, para lo cual es indecidible si el autómata es reversible y para el cual la dinámica inversa puede requieren vecindarios mucho más grandes que la dinámica de avance. ^[6]Cualquier autómata celular reversible puede ser simulado por un autómata celular de bloque reversible con un mayor número de estados; sin embargo, debido a la indecidibilidad de la reversibilidad para los autómatas celulares sin bloques, no hay límite computable en el radio de las regiones en el autómata sin bloques que corresponden a los bloques en la simulación, y la traducción de una regla sin bloques a una regla de bloque tampoco es computable. ^[7]

Los autómatas celulares de bloques también son un formalismo conveniente para diseñar reglas que, además de la reversibilidad, implementen leyes de conservación como la conservación del número de partículas, conservación del momento, etc. Por ejemplo, si la regla dentro de cada bloque conserva el número de células vivas en el bloque, entonces la evolución global del autómata también conservará el mismo número. Esta propiedad es útil en las aplicaciones de los autómatas celulares a la simulación física. ^[8]

Simulación por autómatas celulares convencionales

Como escriben Toffoli y Margolus, ^[2] el modelo de autómata celular de bloque no introduce ningún poder adicional en comparación con un autómata celular convencional que usa la misma estructura de vecindad en cada paso de tiempo: cualquier autómata celular de bloque puede ser simulado en un autómata celular convencional mediante usando más estados y un vecindario más grande. Específicamente, deje que los dos autómatas usen el mismo entramado de celdas, pero deje que cada estado del autómata convencional especifique el estado del autómata de bloque, la fase de su patrón de cambio de partición y la posición de la celda dentro de su bloque. Por ejemplo, con la vecindad de Margolus, esto aumentaría el número de estados en un factor de ocho: hay cuatro posiciones posibles que una celda puede tomar en su 2 × 2bloque, y dos fases a la partición. Además, sea la vecindad del autómata convencional la unión de los bloques que contienen la celda dada en el autómata celular del bloque. Luego, con esta estructura de vecindad y estado, cada actualización del autómata de bloque puede simularse mediante una única actualización del autómata celular convencional.

Aplicaciones

Los autómatas celulares de bloque se utilizan comúnmente para implementar gases de celosía y otras simulaciones cuasi-físicas, debido a la facilidad de simular restricciones físicas como las leyes de conservación en estos sistemas. ^{[1] [8]} Por ejemplo, el modelo de Margolus puede usarse para simular el modelo de gas reticular HPP, en el que las partículas se mueven en dos direcciones perpendiculares y se dispersan en ángulos rectos cuando chocan entre sí. En la simulación celular de bloque de este modelo, la regla de actualización mueve cada celda a la celda diagonalmente opuesta en su bloque, excepto en el caso de que una celda contenga dos partículas diagonalmente opuestas, en cuyo caso son reemplazadas por el par complementario de diagonalmente opuestas. partículas. De esta forma, las partículas se mueven en diagonal y se dispersan según el modelo HPP.^{[2] [9]} Una regla alternativa que simula el modelo de gas de celosía HPP con movimiento horizontal y vertical de partículas, en lugar de con movimiento diagonal, implica rotar el contenido de cada bloque en sentido horario o antihorario en fases alternas, excepto nuevamente en el caso de que una celda contiene dos partículas diagonalmente opuestas, en cuyo caso permanece sin cambios. ^[2] En cualquiera de estos modelos, la cantidad de movimiento (la suma de los vectores de velocidadde las partículas en movimiento) se conserva, así como su número, una propiedad esencial para la simulación de gases físicos. Sin embargo, los modelos HPP son algo poco realistas como modelo de dinámica de gases, porque tienen reglas de conservación no físicas adicionales: se conserva el momento total dentro de cada línea de movimiento, así como el momento total del sistema en general. Los modelos más complejos basados ​​en la cuadrícula hexagonal evitan este problema. ^[9]

Estos autómatas también se pueden utilizar para modelar el movimiento de granos de arena en pilas de arena y relojes de arena . En esta aplicación, se puede usar un vecindario de Margolus con una regla de actualización que conserva el número de granos dentro de cada bloque de 2 × 2 pero que mueve cada grano lo más abajo posible dentro de su bloque. Si un bloque incluye dos granos que se apilan verticalmente uno encima del otro, la función de transición del autómata lo reemplaza por un bloque en el que los granos están uno al lado del otro, lo que de hecho permite que los montones de arena se vuelquen y se esparzan. Este modelo no es reversible, pero sigue cumpliendo una ley de conservación sobre el número de partículas. ^[10]Una regla modificada, que usa el mismo vecindario pero mueve las partículas hacia los lados tanto como sea posible, permite que las pilas de arena simuladas se extiendan incluso cuando no son muy empinadas. ^[11] También son posibles modelos de pila de arena de autómatas celulares más sofisticados, que incorporan fenómenos como el transporte del viento y la fricción. ^[10]

La aplicación original de Margolus para el modelo de autómata celular de bloque era simular el modelo de bola de billar de cálculo reversible, en el que las señales lógicas booleanas se simulan mediante partículas en movimiento y las puertas lógicas se simulan mediante colisiones elásticas.de esas partículas. Es posible, por ejemplo, realizar cálculos de bola de billar en el modelo de Margolus bidimensional, con dos estados por celda, y con el número de células vivas conservadas por la evolución del modelo. En la regla "BBM" que simula el modelo de bola de billar de esta manera, las señales consisten en células vivas individuales, que se mueven en diagonal. Para lograr este movimiento, la función de transición de bloque reemplaza un bloque que contiene una sola celda viva con otro bloque en el que la celda se ha movido a la esquina opuesta del bloque. De manera similar, las colisiones elásticas se pueden realizar mediante una función de transición de bloque que reemplaza dos celdas vivas diagonalmente opuestas por las otras dos celdas del bloque. En todas las demás configuraciones de un bloque, la función de transición de bloque no cambia su estado. En este modelo,2 × 4los rectángulos de células vivas (cuidadosamente alineados con respecto a la partición) permanecen estables y pueden usarse como espejos para guiar las trayectorias de las partículas en movimiento. Por ejemplo, la ilustración de la vecindad de Margolus muestra cuatro partículas y un espejo; si el siguiente paso usa la partición azul, entonces dos partículas se mueven hacia el espejo mientras que las otras dos están a punto de chocar, mientras que si el siguiente paso usa la partición roja, entonces dos partículas se alejan del espejo y las otras dos tienen simplemente chocaron y se separarán unos de otros. ^{[3] [5] [12]}

Reglas adicionales

Los planeadores escapan de una semilla aleatoria central, más allá de los escombros de accidentes de planeadores anteriores, en la regla Critters.

Toffoli y Margolus ^[2] sugieren dos reglas más reversibles para la vecindad de Margolus con células de dos estados que, aunque no están motivadas por consideraciones físicas, conducen a dinámicas interesantes.

Bichos

Artículo principal: Critters (autómata celular)

En la regla "Critters", la función de transición invierte el estado de cada celda en un bloque, excepto para un bloque con exactamente dos celdas vivas que permanece sin cambios. Además, los bloques con tres celdas vivas se someten a una rotación de 180 grados, así como a la inversión de estado. ^[2] Esta es una regla reversible y obedece las leyes de conservación sobre el número de partículas (contando una partícula como una célula viva en fases pares y como una célula muerta en fases impares) y sobre la paridad del número de partículas a lo largo de la diagonal. líneas. ^[12]Debido a que es reversible, los estados iniciales en los que todas las células toman estados elegidos al azar permanecen desestructurados a lo largo de su evolución. Sin embargo, cuando se comienza con un campo más pequeño de células aleatorias centradas dentro de una región más grande de células muertas, esta regla conduce a dinámicas complejas similares a las del Juego de la vida de Conway en el que muchos patrones pequeños similares al planeador de la vida escapan del área aleatoria central y Interactuar el uno con el otro. ^{[2] [12]}A diferencia de los planeadores en Life, la reversibilidad y la conservación de partículas juntas implican que cuando los planeadores chocan juntos en Critters, al menos uno debe escapar y, a menudo, estos choques permiten que ambos planeadores entrantes se reconstituyan en diferentes trayectorias de salida. Mediante tales colisiones, esta regla también puede simular el modelo de computación de la bola de billar, aunque de una manera más compleja que la regla BBM. ^[12] La regla Critters también puede admitir naves espaciales más complejas de diferentes velocidades, así como osciladores con infinitos períodos diferentes. ^[13]

Tron

Las formas rectilíneas generadas por la regla de Tron.

En la regla "Tron", la función de transición deja cada bloque sin cambios, excepto cuando las cuatro celdas tienen el mismo estado, en cuyo caso todos sus estados se invierten. Ejecutar esta regla a partir de las condiciones iniciales en forma de un rectángulo de células vivas, o de formas similares simples de bordes rectos, conduce a patrones rectilíneos complejos. Toffoli y Margolus también sugieren que esta regla se puede usar para implementar una regla de sincronización local que permita simular cualquier autómata celular de bloques de vecindad de Margolus usando un autómata celular asincrónico . En esta simulación, cada celda de un autómata asíncrono almacena tanto un estado para el autómata simulado como un segundo bit que representa la paridadde una marca de tiempo para esa celda; por lo tanto, el autómata asincrónico resultante tiene el doble de estados que el autómata que simula. Las marcas de tiempo están limitadas a diferir como máximo en una entre celdas adyacentes, y cualquier bloque de cuatro celdas cuyas marcas de tiempo tengan la paridad correcta puede actualizarse de acuerdo con la regla de bloque que se está simulando. Cuando se realiza una actualización de este tipo, las paridades de la marca de tiempo también deben actualizarse de acuerdo con la regla Tron, que necesariamente preserva la restricción en las marcas de tiempo adyacentes. Al realizar actualizaciones locales de esta manera, la evolución de cada celda en el autómata asíncrono es idéntica a su evolución en el autómata de bloque síncrono que se está simulando. ^{[2] [14]}

Los tres primeros pasos de la secuencia de los mondadientes y su emulación por un autómata celular de bloque con el barrio de Margolus

Ver también

• Secuencia de palillo de dientes , un patrón fractal que puede ser emulado por autómatas celulares con la vecindad de Margolus

Referencias

1. Schiff, Joel L. (2008), "4.2.1 Partición de autómatas celulares", Autómatas celulares: una visión discreta del mundo , Wiley, págs. 115-116
2. Toffoli, Tommaso ; Margolus, Norman (1987), "II.12 El barrio de Margolus", Máquinas de autómatas celulares: un nuevo entorno para el modelado , MIT Press, págs. 119-138
3. Margolus, N. (1984), "Modelos de computación similares a la física", Physica D , 10 : 81–95, Bibcode : 1984PhyD ... 10 ... 81M , doi : 10.1016 / 0167-2789 (84 ) 90252-5. Reimpreso en Wolfram, Stephen , ed. (1986), Teoría y aplicaciones de los autómatas celulares , Serie avanzada sobre sistemas complejos, 1 , World Scientific, págs. 232–246
4. Morita, K .; Harao, M. (1989), "Computación universalidad de autómatas celulares unidimensionales reversibles (inyectables)", Instituto de Transacciones de Ingenieros de Electrónica, Información y Comunicación, E , 72 : 758–762
5. Durand-Lose, Jérôme (2002), "Computación dentro del modelo de bola de billar", en Adamatzky, Andrew (ed.), Computación basada en colisiones , Springer-Verlag, págs. 135-160
6. Kari, Jarkko (1990), "La reversibilidad de los autómatas celulares 2D es indecidible", Physica D , 45 : 379–385, Bibcode : 1990PhyD ... 45..379K , doi : 10.1016 / 0167-2789 (90) 90195- U
7. Kari, Jarkko (1999), "Sobre la profundidad del circuito de autómatas celulares estructuralmente reversibles", Fundamenta Informaticae , 38 : 93-107; Durand-Lose, Jérôme (2001), "Representación de autómatas celulares reversibles con autómatas celulares de bloques reversibles" , Matemáticas discretas e informática teórica , AA : 145-154, archivado desde el original el 15 de mayo de 2011
8. Wolfram, Stephen (2002), Un nuevo tipo de ciencia , Wolfram Media, págs.  459–464 , ISBN 1-57955-008-8
9. "5.5.4 Lattice Gases", en Schiff (2008) , págs. 165-169.
10. Chopard, Bastien; Droz, Michael (1998), "2.2.6 La regla de la pila de arena", Modelado de sistemas físicos de autómatas celulares , Cambridge University Press, págs. 42-46
11. Gruau, Frédéric; Tromp, John (2000), "Cellular gravity" (PDF) , Parallel Processing Letters , 10 (4): 383–393, doi : 10.1142 / s0129626400000354 , archivado desde el original (PDF) el 18 de julio de 2011
12. Margolus, Norman (1999), "Crystalline Computation", en Hey, Anthony JG (ed.), Feynman and Computation , Perseus Books, págs. 267-305, arXiv : comp-gas / 9811002 , Bibcode : 1998comp.gas.11002M
13. Marotta, Sebastian M. (2005), "Living in Critters 'world" , Revista Ciências Exatas e Naturais , 7 (1), archivado desde el original el 19 de marzo de 2012
14. Ojala, Leo; Penttinen, Olli-Matti; Parviainen, Elina (2004), "Modelado y análisis de autómatas celulares cuánticos de Margolus utilizando métodos teóricos de la red", Aplicaciones y teoría de las redes de Petri 2004 , Lecture Notes in Computer Science, 3099 , Springer-Verlag, págs. 331–350, doi : 10.1007 / 978-3-540-27793-4_19

enlaces externos

• Simulación de bichos , Seth Koehler, Univ. de Florida