Consistencia local

En la satisfacción de restricciones , las condiciones de consistencia local son propiedades de los problemas de satisfacción de restricciones relacionados con la consistencia de subconjuntos de variables o restricciones. Se pueden utilizar para reducir el espacio de búsqueda y facilitar la resolución del problema. Se aprovechan varios tipos de condiciones de coherencia local, incluida la coherencia del nodo , la coherencia del arco y la coherencia de la ruta .

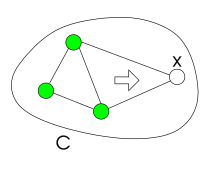
Cada condición de coherencia local se puede imponer mediante una transformación que cambie el problema sin cambiar sus soluciones. Esta transformación se denomina propagación de restricciones . La propagación de restricciones funciona reduciendo dominios de variables, fortaleciendo restricciones o creando nuevas. Esto conduce a una reducción del espacio de búsqueda, lo que hace que el problema sea más fácil de resolver mediante algunos algoritmos. La propagación de restricciones también se puede utilizar como un verificador de insatisfacción, incompleta en general pero completa en algunos casos particulares.

Las condiciones de coherencia local se pueden agrupar en varias clases. Las condiciones de coherencia local originales requieren que cada asignación coherente se pueda extender de forma coherente a otra variable. La consistencia direccional solo requiere que se cumpla esta condición cuando la otra variable sea superior a las de la asignación, según un orden determinado. La consistencia relacional incluye extensiones a más de una variable, pero esta extensión solo es necesaria para satisfacer una restricción determinada o un conjunto de restricciones.

En este artículo, un problema de satisfacción de restricciones se define como un conjunto de variables, un conjunto de dominios y un conjunto de restricciones. Las variables y los dominios están asociados: el dominio de una variable contiene todos los valores que la variable puede tomar. Una restricción se compone de una secuencia de variables, llamada su alcance, y un conjunto de sus evaluaciones, que son las evaluaciones que satisfacen la restricción.

Se supone que los problemas de satisfacción de restricciones a los que se hace referencia en este artículo tienen una forma especial. Un problema está en forma normalizada , respectivamente en forma regular , si cada secuencia de variables es el alcance de como máximo una restricción o exactamente una restricción. El supuesto de regularidad realizado solo para restricciones binarias conduce a la forma estandarizada . Estas condiciones siempre se pueden hacer cumplir combinando todas las restricciones sobre una secuencia de variables en una sola y / o agregando una restricción que se satisfaga con todos los valores de una secuencia de variables.

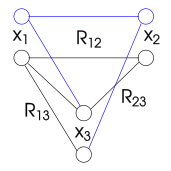
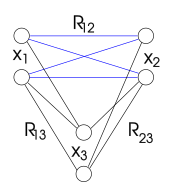
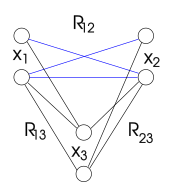
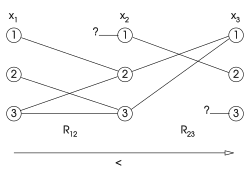
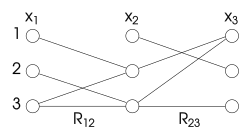
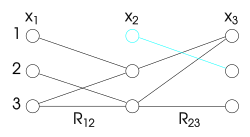
En las cifras utilizadas en este artículo, la falta de vínculos entre dos variables indica que entre estas dos variables no existe una restricción o una restricción satisfecha por todos los valores. [ aclaración necesaria ]

x2 es coherente con x3 pero no con x1, ya que el valor x2 = 1 no corresponde a ningún valor para x1.
La consistencia del arco se aplica al eliminar 1 como valor para x2. Como resultado, x3 ya no es coherente con x2 porque x3 = 2 no corresponde a un valor para x2.
x1 y x2 no son coherentes con la ruta de x3. Se pueden hacer que la trayectoria sea consistente eliminando los valores azules de R12.
Dos variables que no están en una restricción pueden considerarse relacionadas por una restricción virtual que permite cualquier posible par de valores, representados por los bordes azules en esta figura.
Hacer cumplir la consistencia de la ruta de x1 y x2 con x3 elimina el borde en la parte superior. Los valores de x1 y x2 ya no son libres, sino que están relacionados por una nueva restricción real.
Esta instancia es coherente con el arco y no contiene ningún dominio vacío, pero no tiene solución. Las líneas azules indican asignaciones forzadas por la opción x1 = 1.
Una instancia que es coherente con el arco direccional según el orden x1 x2 x3 pero no con coherencia con el arco (no hay ninguna restricción entre x1 y x3; se omiten los bordes correspondientes). Cada valor de una variable de índice más bajo corresponde a valores de variables de índice más alto. Los signos de interrogación indican puntos donde lo contrario no se sostiene.
Las líneas azules indican que no hay restricción entre x3 y x4, por lo que se permiten todos los pares de valores. En estas imágenes, la falta de bordes entre dos variables indica implícitamente la falta de una restricción. Este problema tiene un ancho de 2.
Hacer cumplir la coherencia en x5 elimina la línea roja, creando así una nueva restricción no trivial entre x3 y x4. Como resultado, x4 tiene x3 como nuevo padre, además de x1 y x2. Este cambio aumenta el ancho a 3.
I-consistencia (regular): si una evaluación es consistente, puede extenderse a otra variable de tal manera que se satisfagan todas las restricciones relevantes.
Consistencia del arco relacional: si una evaluación de las variables de una restricción, pero una es consistente, siempre se puede extender a esa variable de tal manera que se satisfaga la restricción . Los bordes cian representan restricciones que no deben ser satisfechas por la extensión.
Una matriz convexa de fila: los 1 de cada fila son contiguos (no hay 0 entre ellos).
Cada matriz representa la restricción entre x i y x k +1 . Si a 1 ... a k son valores para x 1 ... x k , las filas de a 1 ... a k en cada matriz indican los valores permitidos para x k +1 . La convexidad de filas y la fuerte consistencia de la ruta relacional implican la existencia de un valor consistente a k +1 para x k +1 .