número catalán

En matemáticas combinatorias , los números catalanes son una secuencia de números naturales que ocurren en varios problemas de conteo , a menudo involucrando objetos definidos recursivamente . Llevan el nombre del matemático franco-belga Eugène Charles Catalan (1814–1894).

que es equivalente a la expresión dada anteriormente porque . Esta expresión muestra que C _n es un número entero , lo que no es inmediatamente obvio a partir de la primera fórmula dada. Esta expresión forma la base para una prueba de la exactitud de la fórmula .${\displaystyle {\tbinom {2n}{n+1}}={\tfrac {n}{n+1}}{\tbinom {2n}{n}}}$

Los únicos números catalanes C _n que son impares son aquellos para los que n  = 2 ^k  − 1; todos los demás son pares. Los únicos números primos catalanes son C ₂ = 2 y C ₃ = 5. ^[1]

La última representación está estrechamente relacionada con la ley del semicírculo de Wigner para la distribución de valores propios de matrices simétricas aleatorias.

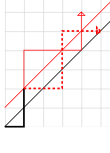
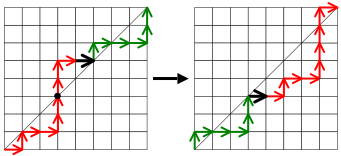
Hay muchos problemas de conteo en combinatoria cuya solución viene dada por los números catalanes. El libro Enumerative Combinatorics: Volume 2 del combinatorialista Richard P. Stanley contiene un conjunto de ejercicios que describen 66 interpretaciones diferentes de los números catalanes. A continuación se presentan algunos ejemplos, con ilustraciones de los casos C ₃  = 5 y C ₄  = 14.

Además, el interior de la Y de cierre que coincide correctamente para la primera X de una palabra de Dyck contiene la descripción del subárbol izquierdo, y el exterior describe el subárbol derecho.

El C ₅ = 42 particiones que no se cruzan de un conjunto de 5 elementos (abajo, las otras 10 de las 52 particiones )

Enrejado de las 14 palabras de Dyck de longitud 8 - ( y ) interpretadas como arriba y abajo

El asociaedro de orden 4 con el C ₄ =14 árboles binarios completos con 5 hojas

El triángulo oscuro es el nodo raíz, los triángulos claros corresponden a los nodos internos de los árboles binarios y las barras verdes son las hojas.

Figura 1. La parte no válida de la ruta (rojo punteado) se invierte (rojo continuo). Los malos caminos (después del cambio) alcanzan ( n  – 1,  n  + 1) en lugar de ( n , n ).

Figura 2. Un camino con excedencia 5.

Figura 3. Las porciones verde y roja se intercambian.

Figura 4. Todos los caminos monótonos en una cuadrícula de 3×3, que ilustran el algoritmo de disminución de excedencia.

Números catalanes en el libro de Mingantu El método rápido para obtener la razón precisa de la división de un círculo volumen III