Teorema del corte de proyección

Teorema de la rebanada de Fourier

En matemáticas , el teorema de proyección-rebanada , teorema central de la rebanada o de Fourier teorema rebanada en dos estados dimensiones que los resultados de los dos cálculos siguientes son iguales:

• Tome una función bidimensional f ( r ), proyéctela (por ejemplo, usando la transformada de Radon ) en una línea (unidimensional) y haga una transformada de Fourier de esa proyección.
• Tome esa misma función, pero primero haga una transformada de Fourier bidimensional y luego córtela a través de su origen, que es paralelo a la línea de proyección.

En términos de operador, si

• F ₁ y F ₂ son los operadores de transformada de Fourier de 1 y 2 dimensiones mencionados anteriormente,
• P ₁ es el operador de proyección (que proyecta una función 2-D en una línea 1-D),
• S ₁ es un operador de corte (que extrae un corte central 1-D de una función),

luego

${\displaystyle F_{1}P_{1}=S_{1}F_{2}.}$

Esta idea se puede extender a dimensiones superiores.

Este teorema se utiliza, por ejemplo, en el análisis de tomografías computarizadas médicas donde una "proyección" es una imagen de rayos X de un órgano interno. Se ve que las transformadas de Fourier de estas imágenes son cortes a través de la transformada de Fourier de la densidad tridimensional del órgano interno, y estos cortes se pueden interpolar para construir una transformada de Fourier completa de esa densidad. La transformada inversa de Fourier se utiliza luego para recuperar la densidad tridimensional del objeto. Esta técnica fue derivada por primera vez por Ronald N. Bracewell en 1956 para un problema de radioastronomía. ^[1]

El teorema del corte de proyección en N dimensiones

En N dimensiones, el teorema del corte de proyección establece que la transformada de Fourier de la proyección de una función N -dimensional f ( r ) en una subvariedad lineal m -dimensional es igual a un corte m -dimensional de la transformada de Fourier N -dimensional de esa función consiste en una subvarietal lineal m -dimensional a través del origen en el espacio de Fourier que es paralelo a la subvarietal de proyección. En términos de operador:

${\displaystyle F_{m}P_{m}=S_{m}F_{N}.\,}$

El teorema generalizado de la rebanada de Fourier

Además de generalizar a N dimensiones, el teorema del corte de proyección se puede generalizar aún más con un cambio arbitrario de base. ^[2] Por conveniencia de la notación, consideramos que el cambio de base se representa como B , una matriz invertible N -por- N que opera en vectores columna N -dimensionales. Entonces, el teorema generalizado de la rebanada de Fourier se puede enunciar como

${\displaystyle F_{m}P_{m}B=S_{m}{\frac {B^{-T}}{|B^{-T}|}}F_{N}}$

donde es la transpuesta de la inversa de la transformada de cambio de base.${\displaystyle B^{-T}=(B^{-1})^{T}}$

Prueba en dos dimensiones

Una ilustración gráfica del teorema del corte de proyección en dos dimensiones. f ( r ) y F ( k ) son pares de transformadas de Fourier bidimensionales. La proyección de f ( r ) en la x eje x es la integral de f ( r ) a lo largo de líneas de visión paralela a la y eje x y la etiqueta es p ( x ). El corte a través de F ( k ) está en el eje k _x , que es paralelo al eje x y está etiquetado como s ( k _x). El teorema del corte de proyección establece que p ( x ) ys ( k _x ) son pares de transformadas de Fourier unidimensionales.

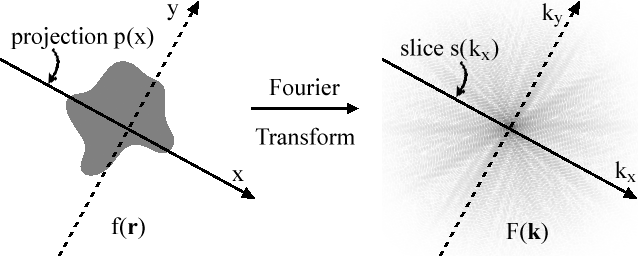
El teorema del corte de proyección se prueba fácilmente para el caso de dos dimensiones. Sin pérdida de generalidad, podemos tomar la línea de proyección como el eje x . No hay pérdida de generalidad porque si usamos una línea desplazada y rotada, la ley aún se aplica. El uso de una línea desplazada (en y) da la misma proyección y, por lo tanto, los mismos resultados de la transformada de Fourier 1D. La función rotada es el par de Fourier de la transformada de Fourier rotada, para la cual el teorema vuelve a ser válido.

Si f ( x ,  y ) es una función bidimensional, entonces la proyección de f ( x ,  y ) sobre el eje x es p ( x ) donde

${\displaystyle p(x)=\int _{-\infty }^{\infty }f(x,y)\,dy.}$

La transformada de Fourier de es${\displaystyle f(x,y)}$

${\displaystyle F(k_{x},k_{y})=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\pi i(xk_{x}+yk_{y})}\,dxdy.}$

La rebanada es entonces ${\displaystyle s(k_{x})}$

${\displaystyle s(k_{x})=F(k_{x},0)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\pi ixk_{x}}\,dxdy}$

${\displaystyle =\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }f(x,y)\,dy\right]\,e^{-2\pi ixk_{x}}dx}$

${\displaystyle =\int _{-\infty }^{\infty }p(x)\,e^{-2\pi ixk_{x}}dx}$

que es solo la transformada de Fourier de p ( x ). La prueba de dimensiones superiores se generaliza fácilmente a partir del ejemplo anterior.

El ciclo de la FHA

Si la función bidimensional f ( r ) es circularmente simétrica, puede representarse como f ( r ), donde r  = | r |. En este caso, la proyección sobre cualquier línea de proyección será la transformada de Abel de f ( r ). La transformada bidimensional de Fourier de f ( r ) será una función circularmente simétrica dada por la transformada de Hankel de orden cero de f ( r), que por lo tanto también representará cualquier corte a través del origen. El teorema del corte de proyección establece que la transformada de Fourier de la proyección es igual al corte o

${\displaystyle F_{1}A_{1}=H,}$

donde A ₁ representa el operador de transformada de Abel, proyectando una función bidimensional circularmente simétrica sobre una línea unidimensional, F ₁ representa el operador de transformada de Fourier 1-D y H representa el operador de transformada de Hankel de orden cero.

Extensión a CT de haz de abanico o haz cónico

El teorema del corte de proyección es adecuado para la reconstrucción de imágenes de TC con proyecciones de haz paralelo. No se aplica directamente a TC de haz de ventilador o haz de cono. El teorema se extendió a la reconstrucción de imágenes de TC en haz de abanico y haz de cono por Shuang-ren Zhao en 1995. ^[3]

Ver también

• Transformada de radón § Relación con la transformada de Fourier

Referencias

1. Bracewell, Ronald N. (1956). "Integración de bandas en radioastronomía" . Revista australiana de física . 9 (2): 198–217. Código bibliográfico : 1956AuJPh ... 9..198B . doi : 10.1071 / PH560198 .
2. Ng, Ren (2005). "Fotografía de Fourier Slice" (PDF) . Transacciones ACM en gráficos . 24 (3): 735–744. doi : 10.1145 / 1073204.1073256 .
3. Zhao SR y H. Halling (1995). Un nuevo método de transformada de Fourier para la tomografía con haz de abanico . Publicado en 1995 en el Simposio de Ciencias Nucleares y el Registro de la Conferencia de Imágenes Médicas . 2 . págs. 1287–91. doi : 10.1109 / NSSMIC.1995.510494 . ISBN 978-0-7803-3180-8.

Otras lecturas

• Bracewell, Ronald N. (1990). "Transformaciones numéricas". Ciencia . 248 (4956): 697–704. Código Bibliográfico : 1990Sci ... 248..697B . doi : 10.1126 / science.248.4956.697 . PMID  17812072 .
• Bracewell, Ronald N. (1956). "Integración de bandas en Radioastronomía" . Aust. J. Phys . 9 (2): 198. Código Bibliográfico : 1956AuJPh ... 9..198B . doi : 10.1071 / PH560198 .
• Gaskill, Jack D. (2005). Sistemas lineales, transformadas de Fourier y óptica . John Wiley & Sons, Nueva York. ISBN 978-0-471-29288-3.
• Ng, Ren (2005). "Fotografía de Fourier Slice" (PDF) . Transacciones ACM en gráficos . 24 (3): 735–744. doi : 10.1145 / 1073204.1073256 .
• Zhao, Shuang-Ren; Halling, Horst (1995). "Reconstrucción de proyecciones de haz cónico con camino de fuente libre por un método de Fourier generalizado". Actas de la reunión internacional de 1995 sobre reconstrucción de imágenes totalmente tridimensionales en radiología y medicina nuclear : 323–7.
• Garcés, Daissy H .; Rhodes, William T .; Peña, Néstor (2011). "El teorema de proyección-rebanada: una notación compacta". Revista de la Sociedad Americana de Óptica A . 28 (5): 766–769. Código Bibliográfico : 2011JOSAA..28..766G . doi : 10.1364 / JOSAA.28.000766 . PMID  21532686 .

enlaces externos

• Teorema de Fourier Slice (video). Parte del curso "Tomografía computarizada y la caja de herramientas ASTRA". Universidad de Amberes . 10 de septiembre de 2015.