Suma de Riemann

En matemáticas , una suma de Riemann es un cierto tipo de aproximación de una integral por una suma finita. Lleva el nombre del matemático alemán del siglo XIX Bernhard Riemann . Una aplicación muy común es aproximar el área de funciones o líneas en un gráfico, pero también la longitud de curvas y otras aproximaciones.

La suma se calcula dividiendo la región en formas ( rectángulos , trapezoides , parábolas o cúbicas ) que juntas forman una región que es similar a la región que se está midiendo, luego se calcula el área para cada una de estas formas y finalmente se suman todas estas pequeñas áreas juntas. Este enfoque se puede usar para encontrar una aproximación numérica para una integral definida incluso si el teorema fundamental del cálculo no facilita encontrar una solución de forma cerrada .

Debido a que la región ocupada por las formas pequeñas no suele tener exactamente la misma forma que la región que se mide, la suma de Riemann diferirá del área que se mide. Este error se puede reducir dividiendo la región más finamente, usando formas cada vez más pequeñas. A medida que las formas se hacen más y más pequeñas, la suma se acerca a la integral de Riemann .

Sea una función definida en un intervalo cerrado de los números reales, , y${\ estilo de visualización f: [a, b] \ flecha derecha \ mathbb {R}}$ ${\ estilo de visualización [a, b]}$${\ estilo de visualización \ mathbb {R}}$

Una suma de Riemann de f sobre I con partición P se define como${\ estilo de visualización S}$

donde y . ^[1] Uno podría producir diferentes sumas de Riemann dependiendo de las que se elijan. Al final esto no importará, si la función es Riemann integrable , cuando la diferencia o ancho de los sumandos se acerque a cero.${\displaystyle \Delta x_{i}=x_{i}-x_{i-1}}$${\displaystyle x_{i}^{*}\en [x_{i-1},x_{i}]}$${\displaystyle x_{i}^{*}}$${\ estilo de visualización \ Delta x_ {i}}$

Cuatro de los métodos de suma de Riemann para aproximar el área bajo las curvas. Los métodos derecho e izquierdo hacen la aproximación utilizando los extremos derecho e izquierdo de cada subintervalo, respectivamente. Los métodos máximo y mínimo realizan la aproximación utilizando los valores de punto final más grande y más pequeño de cada subintervalo, respectivamente. Los valores de las sumas convergen a medida que los subintervalos se reducen a la mitad de arriba a la izquierda a abajo a la derecha.

Suma de Riemann izquierda de x ³ sobre [0,2] usando 4 subdivisiones

Suma de Riemann derecha de x ³ sobre [0,2] usando 4 subdivisiones

Suma de Riemann de punto medio de x ³ sobre [0,2] usando 4 subdivisiones

Suma trapezoidal de Riemann de x ³ sobre [0,2] usando 4 subdivisiones

Comparación de las sumas de la mano derecha de la función y = x ² de 0 a 2 con la integral de la misma de 0 a 2.

Aproximar el área bajo de 0 a 2 usando sumas de la regla correcta. Observe que debido a que la función es monótonamente creciente, las sumas de la mano derecha siempre sobreestimarán el área aportada por cada término en la suma (y lo harán al máximo).${\ estilo de visualización y = x ^ {2}}$

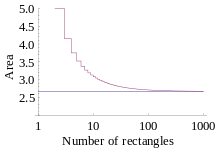
El valor de la suma de Riemann bajo la curva y = x ² de 0 a 2. A medida que aumenta el número de rectángulos, se acerca al área exacta de 8/3.