Problema de Stokes

Problema de Stokes en un fluido viscoso debido a la oscilación armónica de una placa rígida plana (borde inferior negro). Velocidad (línea azul) y excursión de partículas (puntos rojos) en función de la distancia a la pared.

En dinámica de fluidos, el problema de Stokes , también conocido como segundo problema de Stokes o, a veces, denominado capa límite de Stokes o capa límite oscilante, es un problema de determinación del flujo creado por una superficie sólida oscilante, que lleva el nombre de Sir George Stokes . Este se considera uno de los problemas inestables más simples que tienen una solución exacta para las ecuaciones de Navier-Stokes . ^{[1] [2]} En flujo turbulento , esto todavía se llama una capa límite de Stokes, pero ahora uno tiene que confiar en experimentos , simulaciones numéricas o métodos aproximados. para obtener información útil sobre el flujo.

Descripción del flujo ^{[3] [4]}

Considere una placa infinitamente larga que oscila con una velocidad en la dirección, que se encuentra en un dominio infinito de fluido, donde está la frecuencia de las oscilaciones. Las ecuaciones incompresibles de Navier-Stokes se reducen a${\displaystyle U\cos \omega t}$${\displaystyle x}$${\displaystyle y=0}$${\displaystyle \omega }$

${\displaystyle {\frac {\partial u}{\partial t}}=\nu {\frac {\partial ^{2}u}{\partial y^{2}}}}$

donde es la viscosidad cinemática . El gradiente de presión no entra en el problema. La condición inicial, antideslizante en la pared es${\displaystyle \nu }$

${\displaystyle u(0,t)=U\cos \omega t,\quad u(\infty ,t)=0,}$

y la segunda condición de contorno se debe al hecho de que el movimiento en el infinito no se siente. El flujo se debe solo al movimiento de la placa, no hay un gradiente de presión impuesto.${\displaystyle y=0}$

Solución ^{[5] [6]}

La condición inicial no es necesaria debido a la periodicidad. Dado que tanto la ecuación como las condiciones de contorno son lineales, la velocidad se puede escribir como la parte real de alguna función compleja

${\displaystyle u=U\Re \left[e^{i\omega t}f(y)\right]}$

porque .${\displaystyle \cos \omega t=\Re e^{i\omega t}}$

Sustituir esto en la ecuación diferencial parcial lo reduce a ecuación diferencial ordinaria

${\displaystyle f''-{\frac {i\omega }{\nu }}f=0}$

con condiciones de contorno

${\displaystyle f(0)=1,\quad f(\infty )=0}$

La solución al problema anterior es

${\displaystyle f(y)=\exp \left[-{\frac {1+i}{\sqrt {2}}}{\sqrt {\frac {\omega }{\nu }}}y\right]}$

${\displaystyle u(y,t)=Ue^{-{\sqrt {\frac {\omega }{2\nu }}}y}\cos \left(\omega t-{\sqrt {\frac {\omega }{2\nu }}}y\right)}$

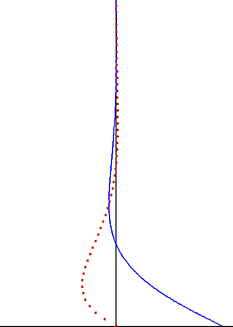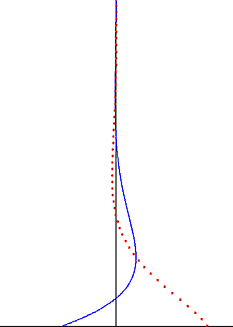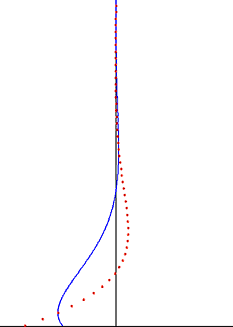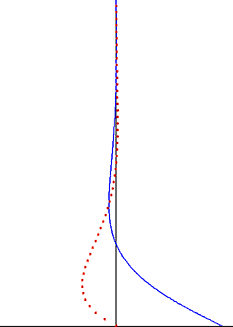
La perturbación creada por la placa oscilante viaja como onda transversal a través del fluido, pero está muy amortiguada por el factor exponencial. La profundidad de penetración de esta onda disminuye con la frecuencia de la oscilación, pero aumenta con la viscosidad cinemática del fluido.${\displaystyle \delta ={\sqrt {2\nu /\omega }}}$

La fuerza por unidad de área ejercida sobre la placa por el fluido es

${\displaystyle F=\mu \left({\frac {\partial u}{\partial y}}\right)_{y=0}={\sqrt {\rho \omega \mu }}U\cos \left(\omega t-{\frac {\pi }{4}}\right)}$

Hay un cambio de fase entre la oscilación de la placa y la fuerza creada.

Oscilaciones de vorticidad cerca del límite

Una observación importante de la solución de Stokes para el flujo de Stokes oscilante es que las oscilaciones de vorticidad se limitan a una capa límite delgada y se humedecen exponencialmente cuando se alejan de la pared. ^[7] Esta observación también es válida para el caso de una capa límite turbulenta. Fuera de la capa límite de Stokes, que a menudo es la mayor parte del volumen de fluido, las oscilaciones de vorticidad pueden despreciarse. Con una buena aproximación, las oscilaciones de la velocidad del flujo son irrotacionales fuera de la capa límite, y la teoría del flujo potencial se puede aplicar a la parte oscilatoria del movimiento. Esto simplifica significativamente la solución de estos problemas de flujo y, a menudo, se aplica en las regiones de flujo de irrigación deondas de sonido y ondas de agua .

Fluido delimitado por una pared superior

Si el dominio del fluido está delimitado por una pared superior estacionaria, ubicada a una altura , la velocidad del flujo está dada por${\displaystyle y=h}$

${\displaystyle u(y,t)={\frac {U}{2(\cosh 2\lambda h-\cos 2\lambda h)}}[e^{-\lambda (y-2h)}\cos(\omega t-\lambda y)+e^{\lambda (y-2h)}\cos(\omega t+\lambda y)-e^{-\lambda y}\cos(\omega t-\lambda y+2\lambda h)-e^{\lambda y}\cos(\omega t+\lambda y-2\lambda h)]}$

donde .${\displaystyle \lambda ={\sqrt {\omega /(2\nu )}}}$

Flujo debido a un gradiente de presión oscilante cerca de una placa rígida plana

Stokes capa límite debido a la oscilación sinusoidal de la velocidad del flujo de campo lejano. La velocidad horizontal es la línea azul y las correspondientes excursiones de partículas horizontales son los puntos rojos.

El caso de un flujo de campo lejano oscilante , con la placa en reposo, se puede construir fácilmente a partir de la solución anterior para una placa oscilante mediante el uso de superposición lineal de soluciones. Considere una oscilación de velocidad uniforme lejos de la placa y una velocidad de fuga en la placa . A diferencia del fluido estacionario en el problema original, el gradiente de presión aquí en el infinito debe ser una función armónica del tiempo. Entonces la solución viene dada por${\displaystyle u(\infty ,t)=U_{\infty }\cos \omega t}$${\displaystyle u(0,t)=0}$

${\displaystyle u(y,t)=U_{\infty }\left[\,\cos \omega t-{\text{e}}^{-{\sqrt {\frac {\omega }{2\nu }}}y}\,\cos \left(\omega t-{\sqrt {\frac {\omega }{2\nu }}}y\right)\right],}$

que es cero en la pared z = 0 , correspondiente a la condición de no deslizamiento para una pared en reposo. Esta situación se encuentra a menudo en ondas de sonido cerca de una pared sólida o para el movimiento de fluidos cerca del lecho marino en ondas de agua . La vorticidad, para el flujo oscilante cerca de una pared en reposo, es igual a la vorticidad en el caso de una placa oscilante pero de signo opuesto.

Problema de Stokes en geometría cilíndrica

Oscilación torsional

Considere un cilindro infinitamente largo de radio que exhibe oscilación torsional con velocidad angular donde está la frecuencia. Luego, la velocidad se acerca después de la fase transitoria inicial a ^[8]${\displaystyle a}$${\displaystyle \Omega \cos \omega t}$${\displaystyle \omega }$

${\displaystyle v_{\theta }=a\Omega \ \Re \left[{\frac {K_{1}(r{\sqrt {i\omega /\nu }})}{K_{1}(a{\sqrt {i\omega /\nu }})}}e^{i\omega t}\right]}$

donde es la función de Bessel modificada del segundo tipo. Esta solución se puede expresar con un argumento real ^[9] como:${\displaystyle K_{1}}$

${\displaystyle {\begin{aligned}v_{\theta }\left(r,t\right)&=\Psi \left\lbrace \left[{\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}r\right)+{\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}r\right)\right]\cos \left(t\right)\right.\\&+\left.\left[{\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}r\right)-{\textrm {ker}}_{1}\left({\sqrt {R_{\omega }}}\right){\textrm {kei}}_{1}\left({\sqrt {R_{\omega }}}r\right)\right]\sin \left(t\right)\right\rbrace \\\end{aligned}}}$

donde

${\displaystyle \Psi =\left[{\textrm {kei}}_{1}^{2}\left({\sqrt {R_{\omega }}}\right)+{\textrm {ker}}_{1}^{2}\left({\sqrt {R_{\omega }}}\right)\right]^{-1},}$

${\displaystyle \mathrm {kei} }$y son funciones de Kelvin y es el número de Reynolds oscilatorio adimensional definido como , siendo la viscosidad cinemática.${\displaystyle \mathrm {ker} }$${\displaystyle R_{\omega }}$${\displaystyle R_{\omega }=\omega a^{2}/\nu }$${\displaystyle \nu }$

Oscilación axial

Si el cilindro oscila en la dirección axial con la velocidad , entonces el campo de velocidad es${\displaystyle U\cos \omega t}$

${\displaystyle u=U\ \Re \left[{\frac {K_{0}(r{\sqrt {i\omega /\nu }})}{K_{0}(a{\sqrt {i\omega /\nu }})}}e^{i\omega t}\right]}$

donde es la función de Bessel modificada del segundo tipo.${\displaystyle K_{0}}$

Flujo de Stokes-Couette ^[10]

En el flujo de Couette , en lugar del movimiento de traslación de una de las placas, se ejecutará una oscilación de un plano. Si tenemos una pared inferior en reposo en y la pared superior en está ejecutando un movimiento oscilatorio con velocidad , entonces el campo de velocidad está dado por${\displaystyle y=0}$${\displaystyle y=h}$${\displaystyle U\cos \omega t}$

${\displaystyle u=U\ \Re \left\{{\frac {\sin ky}{\sin kh}}\right\},\quad {\text{where}}\quad k={\frac {1+i}{\sqrt {2}}}{\sqrt {\frac {\omega }{\nu }}}.}$

La fuerza de fricción por unidad de área en el plano en movimiento es y en el plano fijo es .${\displaystyle -\mu U\Re \{k\cot kh\}}$${\displaystyle \mu U\Re \{k\csc kh\}}$

Ver también

• Problema de Rayleigh

Referencias

1. Wang, CY (1991). "Soluciones exactas de las ecuaciones de Navier-Stokes de estado estacionario". Revisión anual de mecánica de fluidos . 23 : 159-177. Código Bibliográfico : 1991AnRFM..23..159W . doi : 10.1146 / annurev.fl.23.010191.001111 .
2. Landau y Lifshitz (1987), págs. 83–85.
3. Batchelor, George Keith. Introducción a la dinámica de fluidos. Prensa de la universidad de Cambridge, 2000.
4. Lagerstrom, Paco Axel. Teoría del flujo laminar. Prensa de la Universidad de Princeton, 1996.
5. Acheson, David J. Dinámica de fluidos elemental. Prensa de la Universidad de Oxford, 1990.
6. Landau, Lev Davidovich y Evgenii Mikhailovich Lifshitz. "Mecánica de fluidos." (1987).
7. Phillips (1977), pág. 46.
8. Drazin, Philip G. y Norman Riley . Las ecuaciones de Navier-Stokes: una clasificación de flujos y soluciones exactas. No. 334. Cambridge University Press, 2006.
9. Rivero, M .; Garzón, F .; Núñez, J .; Figueroa, A. "Estudio del flujo inducido por cilindro circular realizando oscilación torsional". Revista europea de mecánica - B / Fluids . 78 : 245-251. doi : 10.1016 / j.euromechflu.2019.08.002 .
10. Landau, LD y Sykes, JB (1987). Mecánica de fluidos: Vol 6. págs. 88