Algoritmo de Lloyd

Ejemplo de algoritmo de Lloyd. Se muestra el diagrama de Voronoi de los puntos actuales en cada iteración. Los signos más denotan los centroides de las celdas de Voronoi.

Iteración 2

Iteración 3

Iteración 15

En la última imagen, los puntos están muy cerca de los centroides de las celdas de Voronoi. Se ha encontrado una teselación de Voronoi centroidal.

En ingeniería eléctrica e informática , el algoritmo de Lloyd , también conocido como iteración o relajación de Voronoi , es un algoritmo que lleva el nombre de Stuart P. Lloyd para encontrar conjuntos de puntos espaciados uniformemente en subconjuntos de espacios euclidianos y particiones de estos subconjuntos en formas bien formadas y uniformes. células convexas de tamaño. ^[1] Al igual que el algoritmo de agrupación de k- medias estrechamente relacionado , encuentra repetidamente el centroidede cada conjunto en la partición y luego vuelve a particionar la entrada de acuerdo con cuál de estos centroides es el más cercano. En esta configuración, la operación media es una integral sobre una región del espacio, y la operación de centroide más cercana da como resultado diagramas de Voronoi .

Aunque el algoritmo se puede aplicar más directamente al plano euclidiano , también se pueden aplicar algoritmos similares a espacios de dimensiones superiores oa espacios con otras métricas no euclidianas . El algoritmo de Lloyd se puede utilizar para construir aproximaciones cercanas a las teselaciones de Voronoi centroidales de la entrada, ^[2] que se pueden utilizar para cuantificación , difuminado y punteado . Otras aplicaciones del algoritmo de Lloyd incluyen el suavizado de mallas triangulares en el método de elementos finitos .

Historia

El algoritmo fue propuesto por primera vez por Stuart P. Lloyd de Bell Labs en 1957 como una técnica para la modulación de código de pulso . El trabajo de Lloyd se difundió ampliamente pero permaneció inédito hasta 1982. ^[1] Un algoritmo similar fue desarrollado independientemente por Joel Max y publicado en 1960, ^{[3] por} lo que el algoritmo a veces se conoce como el algoritmo de Lloyd-Max.

Descripción del algoritmo

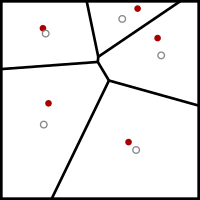
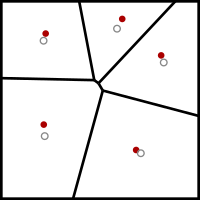
El algoritmo de Lloyd comienza con una ubicación inicial de un número k de sitios puntuales en el dominio de entrada. En aplicaciones de suavizado de malla, estos serían los vértices de la malla que se suavizará; en otras aplicaciones, pueden colocarse al azar o cruzando una malla triangular uniforme del tamaño apropiado con el dominio de entrada.

Luego ejecuta repetidamente el siguiente paso de relajación:

• Se calcula el diagrama de Voronoi de los k sitios.
• Cada celda del diagrama de Voronoi está integrada y se calcula el centroide.
• Luego, cada sitio se mueve al centroide de su celda de Voronoi.

Integración y cálculo de centroides

Debido a que los algoritmos de construcción de diagramas de Voronoi pueden ser muy no triviales, especialmente para entradas de dimensión superior a dos, los pasos para calcular este diagrama y encontrar los centroides exactos de sus celdas pueden reemplazarse por una aproximación.

Aproximación

Una simplificación común es emplear una discretización adecuada del espacio como una fina cuadrícula de píxeles, por ejemplo, el búfer de textura en el hardware gráfico. Las celdas se materializan como píxeles, etiquetados con su correspondiente ID de sitio. El nuevo centro de una celda se aproxima al promediar las posiciones de todos los píxeles asignados con la misma etiqueta. Alternativamente, se pueden utilizar métodos de Monte Carlo , en los que se generan puntos de muestra aleatorios de acuerdo con una distribución de probabilidad subyacente fija, se asignan al sitio más cercano y se promedian para aproximar el centroide de cada sitio.

Cálculo exacto

Aunque también es posible la incrustación en otros espacios, esta elaboración asume el espacio euclidiano utilizando la norma L 2 y discute los dos escenarios más relevantes, que son dos y tres dimensiones respectivamente.

Dado que una celda de Voronoi tiene forma convexa y siempre encierra su sitio, existen descomposiciones triviales en simples simples integrables:

• En dos dimensiones, los bordes de la celda poligonal están conectados con su sitio, creando un conjunto de triángulos en forma de paraguas.
• En tres dimensiones, la celda está rodeada por varios polígonos planos que primero deben triangularse:
  • Calcule un centro para la cara del polígono, por ejemplo, el promedio de todos sus vértices.
  • Al conectar los vértices de una cara poligonal con su centro se obtiene una triangulación plana en forma de paraguas.
  • Trivialmente, un conjunto de tetraedros se obtiene conectando triángulos del casco de la celda con el sitio de la celda.

La integración de una celda y el cálculo de su centroide (centro de masa) ahora se da como una combinación ponderada de los centroides de sus simples (en lo sucesivo llamado ).${\textstyle \mathbf {c} _{i}}$

• Dos dimensiones:
  • Para un triángulo, el centroide se puede calcular fácilmente, por ejemplo, utilizando coordenadas cartesianas .
  • La ponderación se calcula como relaciones de área simplex a celda .
• Tres dimensiones:
  • El centroide de un tetraedro se encuentra como la intersección de tres planos bisectores y se puede expresar como un producto matriz-vector.
  • La ponderación se calcula como relaciones de volumen simplex a celda .

Para una celda 2D con n simples triangulares y un área acumulada (donde es el área de un triángulo simplex), el nuevo centroide de celda se calcula como:${\textstyle A_{C}=\sum _{i=0}^{n}a_{i}}$${\textstyle a_{i}}$

${\displaystyle C={\frac {1}{A_{C}}}\sum _{i=0}^{n}\mathbf {c} _{i}a_{i}}$

De manera análoga, para una celda 3D con un volumen de (donde es el volumen de un tetraedro simplex), el centroide se calcula como:${\textstyle V_{C}=\sum _{i=0}^{n}v_{i}}$${\textstyle v_{i}}$

${\displaystyle C={\frac {1}{V_{C}}}\sum _{i=0}^{n}\mathbf {c} _{i}v_{i}}$

Convergencia

Cada vez que se realiza un paso de relajación, los puntos se dejan en una distribución ligeramente más uniforme: los puntos poco espaciados se alejan más y los puntos muy espaciados se acercan más. En una dimensión, se ha demostrado que este algoritmo converge en un diagrama de Voronoi centroidal, también llamado teselación de Voronoi centroidal . ^[4] En dimensiones superiores, se conocen algunos resultados de convergencia ligeramente más débiles. ^{[5] [6]}

El algoritmo converge lentamente o, debido a limitaciones en la precisión numérica, puede que no converja. Por lo tanto, las aplicaciones del algoritmo de Lloyd en el mundo real normalmente se detienen una vez que la distribución es "suficientemente buena". Un criterio de terminación común es detenerse cuando la distancia máxima movida por cualquier sitio en una iteración cae por debajo de un umbral preestablecido. La convergencia se puede acelerar al relajar demasiado los puntos, lo que se hace moviendo cada punto ω veces la distancia al centro de masa, típicamente usando un valor ligeramente menor que 2 para ω . ^[7]

Aplicaciones

El método de Lloyd se utilizó originalmente para la cuantificación escalar, pero está claro que el método se extiende también a la cuantificación vectorial. Como tal, se utiliza ampliamente en técnicas de compresión de datos en la teoría de la información . El método de Lloyd se usa en gráficos por computadora porque la distribución resultante tiene características de ruido azul (ver también Colores de ruido ), lo que significa que hay pocos componentes de baja frecuencia que podrían interpretarse como artefactos. Es especialmente adecuado para seleccionar posiciones de muestra para difuminar . El algoritmo de Lloyd también se utiliza para generar dibujos de puntos en el estilo de punteado . ^[8]En esta aplicación, los centroides se pueden ponderar en función de una imagen de referencia para producir ilustraciones punteadas que coincidan con una imagen de entrada. ^[9]

En el método de elementos finitos , un dominio de entrada con una geometría compleja se divide en elementos con formas más simples; por ejemplo, los dominios bidimensionales (ya sea subconjuntos del plano euclidiano o superficies en tres dimensiones) a menudo se dividen en triángulos. Es importante para la convergencia de los métodos de elementos finitos que estos elementos tengan una buena forma; en el caso de triángulos, a menudo se prefieren los elementos que son casi triángulos equiláteros. El algoritmo de Lloyd se puede usar para suavizar una malla generada por algún otro algoritmo, moviendo sus vértices y cambiando el patrón de conexión entre sus elementos para producir triángulos que sean más equiláteros. ^[10]Estas aplicaciones suelen utilizar un número menor de iteraciones del algoritmo de Lloyd, deteniéndolo hasta la convergencia, con el fin de preservar otras características de la malla, como las diferencias en el tamaño de los elementos en diferentes partes de la malla. A diferencia de un método de suavizado diferente, el suavizado laplaciano (en el que los vértices de la malla se mueven al promedio de las posiciones de sus vecinos), el algoritmo de Lloyd puede cambiar la topología de la malla, lo que lleva a elementos más casi equiláteros y evita los problemas con enredos que pueden surgir con el alisado laplaciano. Sin embargo, el suavizado laplaciano se puede aplicar de manera más general a mallas con elementos no triangulares.

Diferentes distancias

El algoritmo de Lloyd se usa generalmente en un espacio euclidiano . La distancia euclidiana juega dos roles en el algoritmo: se usa para definir las celdas de Voronoi, pero también corresponde a la elección del centroide como el punto representativo de cada celda, ya que el centroide es el punto que minimiza la distancia euclidiana cuadrática promedio a los puntos en su celda. En su lugar, se pueden utilizar distancias alternativas y puntos centrales alternativos al centroide. Por ejemplo, Hausner (2001) usó una variante de la métrica de Manhattan (con orientaciones que varían localmente) para encontrar un mosaico de una imagen con mosaicos aproximadamente cuadrados cuya orientación se alinea con las características de una imagen, que usó para simular la construcción de mosaicos en mosaico. .^[11] En esta aplicación, a pesar de variar la métrica, Hausner continuó usando centroides como puntos representativos de sus celdas de Voronoi. Sin embargo, para las métricas que difieren más significativamente de las euclidianas, puede ser apropiado elegir el minimizador de la distancia cuadrática promedio como punto representativo, en lugar del centroide. ^[12]

Ver también

• El algoritmo Linde-Buzo-Gray , una generalización de este algoritmo para la cuantificación vectorial
• Recorrido más lejano primero , un método diferente para generar puntos espaciados uniformemente en espacios geométricos
• Desplazamiento medio , un método relacionado para encontrar los máximos de una función de densidad
• K-medias ++

Referencias

1. Lloyd, Stuart P. (1982), "Cuantización de mínimos cuadrados en PCM" (PDF) , IEEE Transactions on Information Theory , 28 (2): 129-137, doi : 10.1109 / TIT.1982.1056489.
2. Du, Qiang ; Faber, Vance; Gunzburger, Max (1999), "Teselaciones centroidales de Voronoi: aplicaciones y algoritmos", Revisión de SIAM , 41 (4): 637–676, Código bibliográfico : 1999SIAMR..41..637D , doi : 10.1137 / S0036144599352836.
3. Max, Joel (1960), "Cuantificación para una distorsión mínima", Transacciones IRE sobre teoría de la información , 6 (1): 7-12, doi : 10.1109 / TIT.1960.1057548.
4. Du, Qiang ; Emelianenko, Maria ; Ju, Lili (2006), "Convergencia del algoritmo de Lloyd para calcular teselaciones de Voronoi centroidales", SIAM Journal on Numerical Analysis , 44 : 102–119, CiteSeerX 10.1.1.591.9903 , doi : 10.1137 / 040617364 .
5. Sabin, MJ; Gray, RM (1986), "Convergencia global y consistencia empírica del algoritmo de Lloyd generalizado", IEEE Transactions on Information Theory , 32 (2): 148-155, doi : 10.1109 / TIT.1986.1057168.
6. Emelianenko, Maria; Ju, Lili; Rand, Alexander (2009), "Nondegeneracy and Weak Global Convergence of the Lloyd Algorithm in R ^d ", SIAM Journal on Numerical Analysis , 46 : 1423–1441, doi : 10.1137 / 070691334.
7. Xiao, Xiao. "Método de Lloyd de relajación excesiva para calcular teselaciones de Voronoi centroidales". (2010).
8. Deussen, Oliver; Hiller, Stefan; van Overveld, Cornelius; Strothotte, Thomas (2000), "Puntos flotantes: un método para calcular dibujos punteados", Computer Graphics Forum , 19 (3): 41–50, doi : 10.1111 / 1467-8659.00396 , Proceedings of Eurographics.
9. Secord, Adrian (2002), "Punteado de Voronoi ponderado", Actas del Simposio sobre animación y renderizado no fotorrealistas (NPAR) , ACM SIGGRAPH , págs. 37-43, doi : 10.1145 / 508530.508537.
10. Du, Qiang ; Gunzburger, Max (2002), "Generación y optimización de cuadrículas basadas en teselaciones de Voronoi centroidales", Matemáticas aplicadas y Computación , 133 (2–3): 591–607, CiteSeerX 10.1.1.324.5020 , doi : 10.1016 / S0096-3003 ( 01) 00260-0 .
11. Hausner, Alejo (2001), "Simulando mosaicos decorativos", Actas de la 28ª conferencia anual sobre gráficos por computadora y técnicas interactivas , ACM SIGGRAPH , págs. 573–580, doi : 10.1145 / 383259.383327.
12. Dickerson, Matthew T .; Eppstein, David ; Wortman, Kevin A. (2010), "Diagramas planos de Voronoi para sumas de funciones convexas, distancia suavizada y dilatación", Proc. Séptimo Simposio Internacional sobre Diagramas de Voronoi en Ciencia e Ingeniería (ISVD 2010) , págs. 13–22, arXiv : 0812.0607 , doi : 10.1109 / ISVD.2010.12.

Enlaces externos

• Simulador gráfico de JavaScript DemoGNG.js para algoritmo LBG y otros modelos, incluye visualización de regiones de Voronoi