Teorema de Berry-Esseen
En la teoría de la probabilidad , el teorema del límite central establece que, en determinadas circunstancias, la distribución de probabilidad de la media escalada de una muestra aleatoria converge a una distribución normal a medida que el tamaño de la muestra aumenta hasta el infinito. Bajo suposiciones más fuertes, el teorema de Berry-Esseen , o la desigualdad de Berry-Esseen , da un resultado más cuantitativo, porque también especifica la velocidad a la que se produce esta convergencia dando un límite al error máximo de aproximación entre la distribución normal y la distribución normal . distribución verdadera de la media muestral escalada. La aproximación se mide por laDistancia Kolmogorov-Smirnov . En el caso de muestras independientes , la tasa de convergencia es n −1/2 , donde n es el tamaño de la muestra, y la constante se estima en términos del tercer momento absoluto normalizado .
Las declaraciones del teorema varían, ya que fue descubierto de forma independiente por dos matemáticos , Andrew C. Berry (en 1941) y Carl-Gustav Esseen (1942), quienes luego, junto con otros autores, lo refinaron repetidamente durante las décadas posteriores.
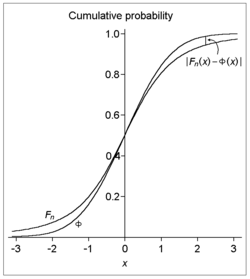
Es decir: dada una secuencia de variables aleatorias independientes e idénticamente distribuidas , cada una con media cero y varianza positiva , si además el tercer momento absoluto es finito, entonces las funciones de distribución acumulativa de la media muestral estandarizada y la distribución normal estándar difieren (verticalmente, en un gráfico) en no más de la cantidad especificada. Tenga en cuenta que el error de aproximación para todo n (y, por lo tanto, la tasa límite de convergencia para n indefinido suficientemente grande) está acotado por el orden de n −1/2 .
Los valores calculados de la constante C han disminuido notablemente a lo largo de los años, desde el valor original de 7,59 de Esseen (1942) , hasta 0,7882 de van Beek (1972) , luego 0,7655 de Shiganov (1986) , luego 0,7056 de Shevtsova (2007) , luego 0.7005 por Shevtsova (2008) , luego 0.5894 por Tyurin (2009) , luego 0.5129 por Korolev & Shevtsova (2010a) , luego 0.4785 por Tyurin (2010) . La revisión detallada se puede encontrar en los documentos Korolev & Shevtsova (2010a) y Korolev & Shevtsova (2010b) . La mejor estimación a partir de 2012 [actualizar], C < 0.4748, se sigue de la desigualdad
Es fácil asegurarse de que ψ 0 ≤ψ 1 . Debido a esta circunstancia, la desigualdad (3) se denomina convencionalmente desigualdad de Berry-Esseen, y la cantidad ψ 0 se denomina fracción de Lyapunov de tercer orden. Además, en el caso de que los sumandos X 1 , ..., X n tengan distribuciones idénticas
Los límites superiores para C 0 se redujeron posteriormente de la estimación original 7,59 debido a Esseen (1942) a (considerando solo los resultados recientes) 0,9051 debido a Zolotarev (1967) , 0,7975 debido a van Beek (1972) , 0,7915 debido a Shiganov (1986) ) , 0,6379 y 0,5606 debido a Tyurin (2009) y Tyurin (2010) . A partir de 2011 [actualizar], la mejor estimación es 0,5600 obtenida por Shevtsova (2010) .