Dominio estratégico

Para la estrategia empresarial, consulte Dominancia (economía) .

Este artículo incluye una lista de referencias generales , pero permanece en gran parte sin verificar porque carece de suficientes citas en línea correspondientes . Ayude a mejorar este artículo introduciendo citas más precisas. ( Enero de 2016 ) ( Obtenga información sobre cómo y cuándo eliminar este mensaje de plantilla )

En la teoría de juegos , el dominio estratégico (comúnmente llamado simplemente dominio ) ocurre cuando una estrategia es mejor que otra para un jugador, sin importar cómo jueguen los oponentes de ese jugador. Muchos juegos simples se pueden resolver usando dominancia. Lo contrario, la intransibilidad , ocurre en juegos en los que una estrategia puede ser mejor o peor que otra para un jugador, dependiendo de cómo jueguen los oponentes del jugador.

Terminología

Cuando un jugador intenta elegir la "mejor" estrategia entre una multitud de opciones, ese jugador puede comparar dos estrategias A y B para ver cuál es mejor. El resultado de la comparación es uno de los siguientes:

• B es equivalente a A: elegir B ​​siempre da el mismo resultado que elegir A, sin importar lo que hagan los otros jugadores.
• B domina estrictamente a A: elegir B ​​siempre da mejores resultados que elegir A, sin importar lo que hagan los otros jugadores.
• B domina débilmente a A: elegir B ​​siempre da al menos un resultado tan bueno como elegir A, sin importar lo que hagan los otros jugadores, y hay al menos un conjunto de acciones de los oponentes para las cuales B da un mejor resultado que A. (Fíjese que si B domina estrictamente A, entonces B domina débilmente A. Por lo tanto, podemos decir que "B domina A" como sinónimo de "B domina débilmente A".) ^[1]
• B y A son intransitivos : B y A no son equivalentes, y B ni domina ni está dominado por A. Elegir A es mejor en algunos casos, mientras que elegir B ​​es mejor en otros casos, dependiendo exactamente de cómo el oponente elija tocar. Por ejemplo, B es "lanzar piedra" mientras que A es "tirar tijeras" en Piedra, Papel, Tijeras .
• B está débilmente dominado por A: hay al menos un conjunto de acciones de los oponentes para las que B da un resultado peor que A, mientras que todos los demás conjuntos de acciones de los oponentes dan a A la misma recompensa que B. (La estrategia A domina débilmente a B) .
• B está estrictamente dominado por A: elegir B ​​siempre da un resultado peor que elegir A, sin importar lo que hagan los otros jugadores. (La estrategia A domina estrictamente a B).

Esta noción se puede generalizar más allá de la comparación de dos estrategias.

• La estrategia B es estrictamente dominante si la estrategia B domina estrictamente todas las demás estrategias posibles.
• La estrategia B es débilmente dominante si la estrategia B domina débil o estrictamente todas las demás estrategias, pero algunas (o todas) las estrategias están solo débilmente dominadas por B.
• La estrategia B está estrictamente dominada si existe alguna otra estrategia que domine estrictamente B.
• La estrategia B está débilmente dominada si existe alguna otra estrategia que domine débilmente B.

Estrategia: un plan contingente completo para un jugador en el juego. Un plan contingente completo es una especificación completa del comportamiento de un jugador, que describe cada acción que un jugador tomaría en cada posible punto de decisión. Debido a que los conjuntos de información representan puntos en un juego en los que un jugador debe tomar una decisión, la estrategia de un jugador describe lo que hará ese jugador con cada conjunto de información. ^[2]

Racionalidad: la suposición de que cada jugador actúa de una manera diseñada para lograr lo que más prefiere dadas las probabilidades de varios resultados; von Neumann y Morgenstern demostraron que si estas preferencias satisfacen ciertas condiciones, esto es matemáticamente equivalente a maximizar una recompensa. Un ejemplo sencillo de maximizar la recompensa es el de la ganancia monetaria, pero para el propósito de un análisis de la teoría de juegos, esta recompensa puede tener cualquier resultado deseado. Por ejemplo, recompensa en efectivo, minimización del esfuerzo o la incomodidad, promoción de la justicia o acumulación de "utilidad" general: el supuesto de racionalidad establece que los jugadores siempre actuarán de la manera que mejor satisfaga su orden del mejor al peor de los diversos resultados posibles. ^[2]

Conocimiento común : la suposición de que cada jugador tiene conocimiento del juego, conoce las reglas y los beneficios asociados con cada curso de acción y se da cuenta de que todos los demás jugadores tienen el mismo nivel de comprensión. Esta es la premisa que permite a un jugador hacer un juicio de valor sobre las acciones de otro jugador, respaldado por el supuesto de racionalidad, en consideración al seleccionar una acción. ^[2]

Equilibrios de dominancia y de Nash

	C	D
C	1, 1	0, 0
D	0, 0	0, 0

Si existe una estrategia estrictamente dominante para un jugador en un juego, ese jugador jugará esa estrategia en cada uno de los equilibrios de Nash del juego . Si ambos jugadores tienen una estrategia estrictamente dominante, el juego solo tiene un equilibrio de Nash único. Sin embargo, ese equilibrio de Nash no es necesariamente "eficiente", lo que significa que puede haber resultados del juego sin equilibrio que serían mejores para ambos jugadores. El juego clásico utilizado para ilustrar esto es el Dilema del Prisionero .

Las estrategias estrictamente dominadas no pueden ser parte de un equilibrio de Nash y, como tal, es irracional que cualquier jugador las juegue. Por otro lado, las estrategias débilmente dominadas pueden formar parte de los equilibrios de Nash. Por ejemplo, considere la matriz de pagos que se muestra a la derecha.

La estrategia C domina débilmente la estrategia D. Considere jugar C : si el oponente juega C, uno obtiene 1; si el oponente juega D, uno obtiene 0. Compare esto con D, donde uno obtiene 0 independientemente. Ya que en un caso, uno hace mejor al jugar C en lugar de D y nunca lo hace peor, C domina débilmente D . A pesar de esto, es un equilibrio de Nash. Supongamos que ambos jugadores eligen D . Ninguno de los jugadores mejorará si se desvía unilateralmente: si un jugador cambia a jugar C,${\displaystyle (D,D)}$todavía obtendrán 0. Esto satisface los requisitos de un equilibrio de Nash. Suponga que ambos jugadores eligen C. A ninguno de los jugadores le irá mejor si se desvía unilateralmente; si un jugador cambia a jugar D, obtendrá 0. Esto también satisface los requisitos de un equilibrio de Nash.

Eliminación iterada de estrategias estrictamente dominadas (IESDS)

La eliminación iterativa (o supresión) de estrategias dominadas (también denominadas IESDS o IDSDS) es una técnica común para resolver juegos que implica la eliminación iterativa de estrategias dominadas. En el primer paso, como máximo se elimina una estrategia dominada del espacio de estrategia de cada uno de los jugadores, ya que ningún jugador racional jugaría estas estrategias. Esto da como resultado un juego nuevo y más pequeño. Algunas estrategias, que antes no estaban dominadas, pueden estar dominadas en el juego más pequeño. Se repite el primer paso, creando un nuevo juego aún más pequeño, y así sucesivamente. El proceso se detiene cuando no se encuentra ninguna estrategia dominada para ningún jugador. Este proceso es válido ya que se asume que la racionalidad entre los jugadores es de conocimiento común, es decir, cada jugador sabe que el resto de los jugadores son racionales, y cada jugador sabe que el resto de los jugadores sabe que sabe que el resto de los jugadores son racionales, y así ad infinitum (ver Aumann, 1976) .

Hay dos versiones de este proceso. Una versión implica solo eliminar las estrategias estrictamente dominadas. Si, después de completar este proceso, solo queda una estrategia para cada jugador, ese conjunto de estrategias es el equilibrio de Nash único. ^[3]

Ejemplo paso a paso de eliminación de dominancia estricta:

1. C está estrictamente dominado por A para el jugador 1. Por lo tanto, el jugador 1 nunca jugará la estrategia C. El jugador 2 lo sabe. (ver IESDS Figura 1)
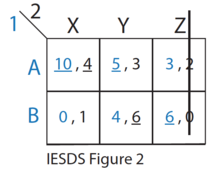
2. De las estrategias restantes (ver IESDS Figura 2), Z está estrictamente dominada por Y y X para el jugador 2. Por lo tanto, el jugador 2 nunca jugará la estrategia Z. El jugador 1 lo sabe.
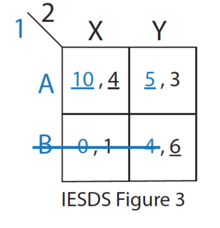
3. De las estrategias restantes (ver IESDS Figura 3), B está estrictamente dominada por A para el jugador 1. Por lo tanto, el jugador 1 nunca jugará B. El jugador 2 lo sabe.
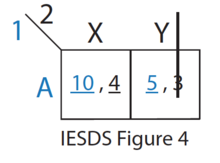
4. De las estrategias restantes (ver IESDS Figura 4), Y está estrictamente dominada por X para el jugador 2. Por lo tanto, el jugador 2 nunca jugará con Y. El jugador 1 lo sabe.
5. Solo queda una estrategia racionalizable {A, X} que da como resultado una recompensa de (10,4). Este es el único equilibrio de Nash para este juego.

Otra versión implica la eliminación de estrategias dominadas tanto estricta como débilmente. Si, al final del proceso, hay una única estrategia para cada jugador, este conjunto de estrategias también es un equilibrio de Nash . Sin embargo, a diferencia del primer proceso, la eliminación de estrategias débilmente dominadas puede eliminar algunos equilibrios de Nash. Como resultado, el equilibrio de Nash encontrado al eliminar estrategias débilmente dominadas puede no ser el único equilibrio de Nash. (En algunos juegos, si eliminamos estrategias débilmente dominadas en un orden diferente, podemos terminar con un equilibrio de Nash diferente).

Ejemplo paso a paso de eliminación de dominancia débil:

1. O está estrictamente dominado por N para el jugador 1. Por lo tanto, el jugador 1 nunca jugará la estrategia O. El jugador 2 lo sabe. (ver IESDS Figura 5)
2. U está débilmente dominado por T para el jugador 2. Si el jugador 2 elige T, entonces el equilibrio final es (N, T)

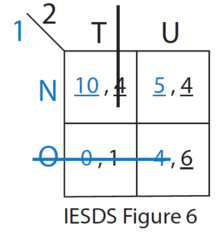
1. O está estrictamente dominado por N para el jugador 1. Por lo tanto, el jugador 1 nunca jugará la estrategia O. El jugador 2 lo sabe. (ver IESDS Figura 6)
2. T está débilmente dominado por U para el jugador 2. Si el jugador 2 elige U, entonces el equilibrio final es (N, U)

En cualquier caso, si mediante la eliminación iterativa de las estrategias dominadas solo queda una estrategia para cada jugador, el juego se denomina juego con solución por dominancia .

Ver también

• Arbitraje
• Estrategia dominada por Max
• La paradoja de Newcomb
• Dominio del riesgo
• Estrategia ganadora

Referencias

1. Leyton-Brown, Kevin; Shoham, Yoav (enero de 2008). "Fundamentos de la teoría de juegos: una introducción multidisciplinar concisa". Conferencias de síntesis sobre inteligencia artificial y aprendizaje automático . 2 (1): 36. doi : 10.2200 / S00108ED1V01Y200802AIM003 .
2. Joel, Watson (9 de mayo de 2013). Estrategia: Introducción a la teoría de juegos (Tercera ed.). Nueva York. ISBN 9780393918380. OCLC  842323069 .
3. Joel., Watson ,. Estrategia: una introducción a la teoría de juegos (Segunda ed.). Nueva York. ISBN 9780393929348 . 

• Fudenberg, Drew; Tirole, Jean (1993). Teoría de juegos . Prensa del MIT.
• Gibbons, Robert (1992). Teoría de juegos para economistas aplicados . Prensa de la Universidad de Princeton. ISBN 0-691-00395-5.
• Gintis, Herbert (2000). Evolución de la teoría de juegos . Prensa de la Universidad de Princeton. ISBN 0-691-00943-0.
• Leyton-Brown, Kevin; Shoham, Yoav (2008). Fundamentos de la teoría de juegos: una introducción concisa y multidisciplinaria . San Rafael, CA: Morgan & Claypool Publishers. ISBN 978-1-59829-593-1.. Una introducción matemática de 88 páginas; consulte la Sección 3.3. Gratis en línea en muchas universidades.
• Rapoport, A. (1966). Teoría de juegos para dos personas: las ideas esenciales . Prensa de la Universidad de Michigan.
• Curso de teoría de juegos de Jim Ratliff: dominio estratégico
• Shoham, Yoav; Leyton-Brown, Kevin (2009). Sistemas multiagente: fundamentos algorítmicos, teóricos de juegos y lógicos . Nueva York: Cambridge University Press . ISBN 978-0-521-89943-7.. Una referencia integral desde una perspectiva computacional; consulte las Secciones 3.4.3, 4.5. Descarga gratuita en línea .

Este artículo incorpora material de la estrategia dominante en PlanetMath , que está bajo la licencia Creative Commons Attribution / Share-Alike License .