Regresión isotónica

Tipo de análisis numérico

Este artículo proporciona un contexto insuficiente para quienes no están familiarizados con el tema . Por favor, ayuda a mejorar el artículo por proporcionar más contexto para el lector . ( Febrero de 2012 ) ( Obtenga información sobre cómo y cuándo eliminar este mensaje de plantilla )

Un ejemplo de regresión isotónica (línea roja continua) en comparación con la regresión lineal en los mismos datos, ambos se ajustan para minimizar el error cuadrático medio . La propiedad de forma libre de la regresión isotónica significa que la línea puede ser más empinada donde los datos son más empinados; la restricción de isotonicidad significa que la línea no disminuye.

Parte de una serie sobre
Análisis de regresión
Modelos
Regresión lineal Regresión simple Regresión polinomial Modelo linear general
Modelo lineal generalizado Elección discreta Regresión binomial Regresión binaria Regresión logística Logit multinomial Logit mixto Probit Probit multinomial Logit ordenado Probit ordenado Poisson
Modelo multinivel Efectos fijos Efectos aleatorios Modelo lineal de efectos mixtos Modelo no lineal de efectos mixtos
Regresión no lineal No paramétrico Semiparamétrico Robusto Cuantil Isotónico Componentes principales Menor ángulo Local Segmentario
Errores en variables
Estimacion
Mínimos cuadrados Lineal No lineal
Ordinario Ponderado Generalizado
Parcial Total No negativo Regresión de crestas Regularizado
Desviaciones mínimas absolutas Reponderado iterativamente Bayesiano Multivariado bayesiano
Fondo
Validación de regresión Respuesta media y prevista Errores y residuales Bondad de ajuste Residuo estudentizado Teorema de Gauss-Markov
Portal de matemáticas
v t mi

En estadísticas , regresión isotónica o monotónica de regresión es la técnica de ajuste de una línea de forma libre a una secuencia de observaciones de tal manera que la línea ajustada es no decreciente (o no creciente) en todas partes, y la mentira como cerca de las observaciones como sea posible.

Aplicaciones

La regresión isotónica tiene aplicaciones en inferencia estadística . Por ejemplo, se podría usar para ajustar una curva isotónica a las medias de algún conjunto de resultados experimentales cuando se espera un aumento de esas medias de acuerdo con algún orden en particular. Una ventaja de la regresión isotónica es que no está limitada por ninguna forma funcional, como la linealidad impuesta por la regresión lineal , siempre que la función sea monótona creciente.

Otra aplicación es el escalado multidimensional no métrico , ^[1] donde se busca una incrustación de baja dimensión para los puntos de datos de manera que el orden de las distancias entre los puntos en la incrustación coincida con el orden de disimilitud entre los puntos. La regresión isotónica se usa iterativamente para ajustar distancias ideales para preservar el orden relativo de disimilitud.

La regresión isotónica también se utiliza en la clasificación probabilística para calibrar las probabilidades predichas de los modelos de aprendizaje automático supervisados . ^[2]

La regresión isotónica para el caso simplemente ordenado con univariante se ha aplicado para estimar las relaciones continuas de dosis-respuesta en campos como la anestesiología y la toxicología. Hablando en términos estrictos, la regresión isotónica solo proporciona estimaciones puntuales en los valores observados. La estimación de la curva completa de respuesta a la dosis sin suposiciones adicionales se realiza generalmente mediante interpolación lineal entre las estimaciones puntuales. ^[3]${\displaystyle x,y}$${\displaystyle x.}$

Se ha desarrollado un software para calcular la regresión isotónica (monótona) para R , ^{[4] [5]} Stata y Python . ^[6]

Enunciado del problema y algoritmos

Sea un conjunto dado de observaciones, donde el y el caen en algún conjunto parcialmente ordenado . En general, a cada observación se le puede dar un peso , aunque comúnmente para todas . ${\displaystyle (x_{1},y_{1}),\ldots ,(x_{n},y_{n})}$${\displaystyle y_{i}\in \mathbb {R} }$${\displaystyle x_{i}}$${\displaystyle (x_{i},y_{i})}$${\displaystyle w_{i}\geq 0}$${\displaystyle w_{i}=1}$${\displaystyle i}$

La regresión isotónica busca un ajuste de mínimos cuadrados ponderados para todos , sujeto a la restricción de que siempre . Esto da el siguiente programa cuadrático (QP) en las variables :${\displaystyle {\hat {y}}_{i}\approx y_{i}}$${\displaystyle i}$${\displaystyle {\hat {y}}_{i}\leq {\hat {y}}_{j}}$${\displaystyle x_{i}\leq x_{j}}$${\displaystyle {\hat {y}}_{1},\ldots ,{\hat {y}}_{n}}$

${\displaystyle \min \sum _{i=1}^{n}w_{i}({\hat {y}}_{i}-y_{i})^{2}}$ sujeto a ${\displaystyle {\hat {y}}_{i}\leq {\hat {y}}_{j}{\text{ for all }}(i,j)\in E}$

donde especifica el orden parcial de las entradas observadas (y puede considerarse como el conjunto de aristas de algún gráfico dirigido con vértices ). Los problemas de esta forma pueden resolverse mediante técnicas genéricas de programación cuadrática.${\displaystyle E=\{(i,j):x_{i}\leq x_{j}\}}$${\displaystyle x_{i}}$${\displaystyle 1,2,\ldots n}$

En el escenario habitual donde los valores caen en un conjunto totalmente ordenado como , podemos asumir WLOG que las observaciones se han ordenado de modo que , y tome . En este caso, un algoritmo iterativo simple para resolver el programa cuadrático es el algoritmo de infractores adyacentes al grupo . Por el contrario, Best y Chakravarti ^[7] estudiaron el problema como un problema de identificación de conjuntos activos y propusieron un algoritmo primario. Estos dos algoritmos pueden verse como el dual del otro, y ambos tienen una complejidad computacional de datos ya ordenados. ^[7]${\displaystyle x_{i}}$${\displaystyle \mathbb {R} }$${\displaystyle x_{1}\leq x_{2}\leq \cdots \leq x_{n}}$${\displaystyle E=\{(i,i+1):1\leq i<n\}}$${\displaystyle O(n)}$

Para completar la tarea de regresión isotónica, entonces podemos elegir cualquier función no decreciente tal que para todo i. Cualquiera de estas funciones obviamente resuelve${\displaystyle f(x)}$${\displaystyle f(x_{i})={\hat {y}}_{i}}$

${\displaystyle \min _{f}\sum _{i=1}^{n}w_{i}(f(x_{i})-y_{i})^{2}}$sujeto a ser no decreciente${\displaystyle f}$

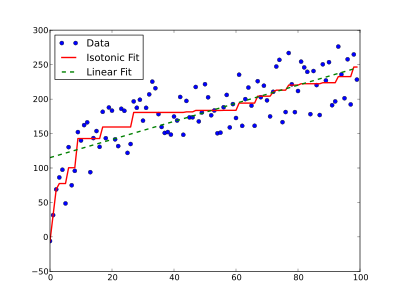
y se puede utilizar para predecir los valores de nuevos valores de . Una elección común cuando sería interpolar linealmente entre los puntos , como se ilustra en la figura, produciendo una función lineal continua por partes:${\displaystyle y}$${\displaystyle x}$${\displaystyle x_{i}\in \mathbb {R} }$${\displaystyle (x_{i},{\hat {y}}_{i})}$

${\displaystyle f(x)={\begin{cases}{\hat {y}}_{1}&{\text{if }}x\leq x_{1}\\{\hat {y}}_{i}+{\frac {x-x_{i}}{x_{i+1}-x_{i}}}({\hat {y}}_{i+1}-{\hat {y}}_{i})&{\text{if }}x_{i}\leq x\leq x_{i+1}\\{\hat {y}}_{n}&{\text{if }}x\geq x_{n}\end{cases}}}$

Regresión isotónica centrada

Como muestra la primera figura de este artículo, en presencia de violaciones de monotonicidad, la curva interpolada resultante tendrá intervalos planos (constantes). En las aplicaciones de respuesta a la dosis, generalmente se sabe que no solo es monótono sino también suave. Los intervalos planos son incompatibles con la forma asumida y se puede demostrar que están sesgados. Oron y Flournoy desarrollaron una mejora simple para tales aplicaciones, denominada regresión isotónica centrada (CIR), que demostró que reduce sustancialmente el error de estimación tanto para aplicaciones de dosis-respuesta como de búsqueda de dosis. ^[8] Tanto CIR como la regresión isotónica estándar para el caso univariante, simplemente ordenado, se implementan en el paquete R "cir". ^[4] Este paquete también proporciona estimaciones analíticas de intervalos de confianza.${\displaystyle f(x)}$${\displaystyle f(x)}$

Referencias

1. Kruskal, JB (1964). "Escalado multidimensional no métrico: un método numérico". Psychometrika . 29 (2): 115-129. doi : 10.1007 / BF02289694 .
2. "Predicción de buenas probabilidades con aprendizaje supervisado | Actas de la 22ª conferencia internacional sobre aprendizaje automático" . dl.acm.org . Consultado el 7 de julio de 2020 .
3. Stylianou, diputado; Flournoy, N (2002). "Hallazgo de dosis utilizando el diseño de moneda sesgada hacia arriba y hacia abajo y regresión isotónica". Biometría . 58 : 171-177. doi : 10.1111 / j.0006-341x.2002.00171.x .
4. Oron, Assaf. "Paquete 'cir ' " . CRAN . Fundación R para la Computación Estadística . Consultado el 26 de diciembre de 2020 .
5. Leeuw, Jan de; Hornik, Kurt; Mair, Patrick (2009). "Optimización isotónica en R: algoritmo de violadores adyacentes de grupo (PAVA) y métodos de conjunto activo" . Revista de software estadístico . 32 (5): 1–24. doi : 10.18637 / jss.v032.i05 . ISSN 1548-7660 . 
6. Pedregosa, Fabián; et al. (2011). "Scikit-learn: aprendizaje automático en Python". Revista de investigación sobre aprendizaje automático . 12 : 2825-2830. arXiv : 1201.0490 . Código bibliográfico : 2012arXiv1201.0490P .
7. Mejor, Michael J .; Chakravarti, Nilotpal (1990). "Algoritmos de conjuntos activos para regresión isotónica; un marco unificador" . Programación matemática . 47 (1–3): 425–439. doi : 10.1007 / bf01580873 . ISSN 0025-5610 . 
8. Oron, AP; Flournoy, N (2017). "Regresión isotónica centrada: estimación de intervalos y puntos para estudios de dosis-respuesta". Estadística en Investigación Biofarmacéutica . 9 : 258-267. arXiv : 1701.05964 . doi : 10.1080 / 19466315.2017.1286256 .

Lectura adicional

• Robertson, T .; Wright, FT; Dykstra, RL (1988). Ordene la inferencia estadística restringida . Nueva York: Wiley. ISBN 978-0-471-91787-8.
• Barlow, RE; Bartolomé, DJ; Bremner, JM; Brunk, HD (1972). Inferencia estadística bajo restricciones de orden; la teoría y aplicación de la regresión isotónica . Nueva York: Wiley. ISBN 978-0-471-04970-8.
• Shively, TS, Sager, TW, Walker, SG (2009). "Un enfoque bayesiano para la estimación de funciones monótonas no paramétricas". Revista de la Sociedad Real de Estadística, Serie B . 71 (1): 159-175. CiteSeerX  10.1.1.338.3846 . doi : 10.1111 / j.1467-9868.2008.00677.x .
• Wu, WB ; Woodroofe, M .; Mentz, G. (2001). "Regresión isotónica: otra mirada al problema del punto de cambio". Biometrika . 88 (3): 793–804. doi : 10.1093 / biomet / 88.3.793 .