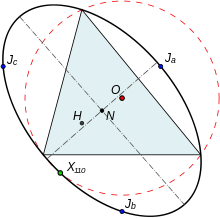
Círculos de Johnson
En geometría , un conjunto de círculos de Johnson comprende tres círculos de igual radio r que comparten un punto común de intersección H. En tal configuración, los círculos suelen tener un total de cuatro intersecciones (puntos donde al menos dos de ellos se encuentran): el punto común H que comparten todos, y para cada uno de los tres pares de círculos un punto de intersección más (referido aquí como su intersección de dos sentidos). Si dos círculos cualesquiera osculan, solo tienen H como punto común, y entonces se considerará que Hsea también su intersección de dos sentidos; si coinciden, declaramos que su intersección en dos sentidos es el punto diametralmente opuesto a H. Los tres puntos de intersección de dos sentidos definen el triángulo de referencia de la figura. El concepto lleva el nombre de Roger Arthur Johnson. [1] [2] [3]
La propiedad 1 es obvia a partir de la definición. La propiedad 2 también es clara: para cualquier círculo de radio r , y cualquier punto P sobre él, el círculo de radio 2 r centrado en P es tangente al círculo en su punto opuesto a P ; esto se aplica en particular a P = H , dando el círculo anticomplementario C. Inmediatamente sigue la propiedad 3 en la formulación de la homotecia; el triángulo de puntos de tangencia se conoce como triángulo anticomplementario.
Para las propiedades 4 y 5, primero observe que dos de los tres círculos de Johnson son intercambiados por la reflexión en la línea que conecta H y su intersección bidireccional (o en su tangente común en H si estos puntos coinciden), y esta reflexión también intercambia los dos vértices del triángulo anticomplementario que se encuentran en estos círculos. Por lo tanto, el punto de intersección de 2 sentidos es el punto medio de un lado del triángulo anticomplementario, y H se encuentra en la bisectriz perpendicularde este lado. Ahora, los puntos medios de los lados de cualquier triángulo son las imágenes de sus vértices por una homotecia con factor −½, centrada en el baricentro del triángulo. Aplicado al triángulo anticomplementario, que a su vez se obtiene del triángulo de Johnson por una homotecia con factor 2, se deduce de la composición de homotecias que el triángulo de referencia es homotético al triángulo de Johnson por un factor -1. Dado que tal homotecia es una congruencia , esto da la propiedad 5, y también el teorema de los círculos de Johnson, ya que los triángulos congruentes tienen círculos circunscritos de igual radio.
Para la propiedad 6, ya se estableció que las bisectrices perpendiculares de los lados del triángulo anticomplementario pasan todas por el punto H ; dado que ese lado es paralelo a un lado del triángulo de referencia, estas bisectrices perpendiculares son también las altitudes del triángulo de referencia.
La propiedad 7 se sigue inmediatamente de la propiedad 6 ya que el centro homotético cuyo factor es -1 debe estar en el punto medio de los circuncentros O del triángulo de referencia y H del triángulo de Johnson; este último es el ortocentro del triángulo de referencia, y se sabe que su centro de nueve puntos es ese punto medio. Dado que la simetría central también asigna el ortocentro del triángulo de referencia al del triángulo de Johnson, el centro homotético también es el centro de nueve puntos del triángulo de Johnson.