Multiplicador de Lagrange

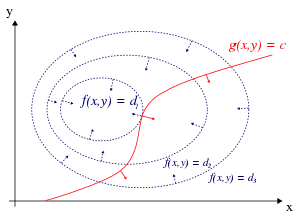
En optimización matemática , el método de los multiplicadores de Lagrange es una estrategia para encontrar los máximos y mínimos locales de una función sujeta a restricciones de igualdad (es decir, sujeta a la condición de que una o más ecuaciones deben satisfacerse exactamente por los valores elegidos de las variables ). ^[1] Lleva el nombre del matemático Joseph-Louis Lagrange . La idea básica es convertir un problema restringido en una forma tal que la prueba de la derivadade un problema sin restricciones todavía se puede aplicar. La relación entre el gradiente de la función y los gradientes de las restricciones conduce de manera bastante natural a una reformulación del problema original, conocida como la función de Lagrangian . ^[2]

El método se puede resumir de la siguiente manera: para encontrar el máximo o mínimo de una función sujeta a la restricción de igualdad , formar la función Lagrangiana${\ estilo de visualización f (x)}$${\ estilo de visualización g (x) = 0}$

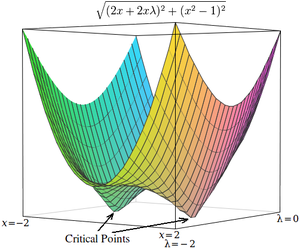
y encuentre los puntos estacionarios ^{[ aclaración necesaria ]} de considerados en función de y el multiplicador de Lagrange . ^[3] La solución correspondiente a la optimización restringida original es siempre un punto silla de la función Lagrangiana, ^{[4] [5]} que se puede identificar entre los puntos estacionarios a partir de la definición de la matriz hessiana bordeada . ^[6]${\displaystyle {\mathcal {L}}}$${\ estilo de visualización x}$${\ estilo de visualización \ lambda}$

La gran ventaja de este método es que permite resolver la optimización sin una parametrización explícita en términos de las restricciones. Como resultado, el método de los multiplicadores de Lagrange se usa ampliamente para resolver problemas desafiantes de optimización con restricciones. Además, el método de los multiplicadores de Lagrange se generaliza mediante las condiciones de Karush-Kuhn-Tucker , que también pueden tener en cuenta las restricciones de desigualdad de la forma .${\displaystyle h(\mathbf {x} )\leq c}$

Sea la función objetivo, sea ​​la función de restricciones, ambas pertenecientes a (es decir, que tienen primeras derivadas continuas). Sea una solución óptima del siguiente problema de optimización tal que rank :${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }$${\displaystyle g\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{c}}$${\ estilo de visualización C^{1}}$${\ estilo de visualización x^{*}}$${\displaystyle Dg(x^{*})=c<n}$

Figura 1: La curva roja muestra la restricción g ( x , y ) = c . Las curvas azules son contornos de f ( x , y ) . El punto donde la restricción roja toca tangencialmente un contorno azul es el máximo de f ( x , y ) a lo largo de la restricción, ya que d ₁ > d ₂ .

Figura 2: Un paraboloide restringido a lo largo de dos líneas que se cruzan.

Figura 3: Mapa de contorno de la Figura 2.

Ilustración del problema de optimización con restricciones 1a

Ilustración del problema de optimización con restricciones 1b

Ilustración del problema de optimización con restricciones

Los multiplicadores de Lagrange hacen que los puntos críticos ocurran en los puntos silla.

La magnitud del gradiente se puede usar para forzar que los puntos críticos ocurran en mínimos locales.