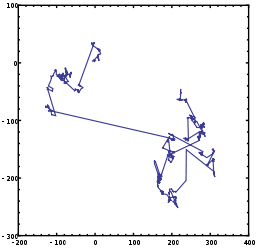
Vuelo de Lévy

Un vuelo Lévy es un paseo aleatorio en el que la etapa de longitudes tienen una distribución Lévy , una distribución de probabilidad que es pesado de cola . Cuando se define como un paseo en un espacio de dimensión mayor que uno, los pasos realizados son en direcciones isotrópicas aleatorias. Investigadores posteriores han ampliado el uso del término "vuelo de Lévy" para incluir también los casos en los que la caminata aleatoria tiene lugar en una cuadrícula discreta en lugar de en un espacio continuo. ^{[1] [2]}

El término "vuelo de Lévy" fue acuñado por Benoît Mandelbrot , ^[3] quien lo utilizó para una definición específica de la distribución de tamaños de paso. Usó el término vuelo de Cauchy para el caso donde la distribución de tamaños de paso es una distribución de Cauchy , ^[4] y vuelo de Rayleigh para cuando la distribución es una distribución normal ^[5] (que no es un ejemplo de una distribución de probabilidad de cola pesada ).

El caso particular para el que Mandelbrot utilizó el término "vuelo de Lévy" ^[3] se define por la función de superviviente (comúnmente conocida como función de supervivencia) de la distribución de tamaños de paso, U , siendo ^[6]

Aquí D es un parámetro relacionado con la dimensión fractal y la distribución es un caso particular de la distribución de Pareto .

Los vuelos de Lévy son, por construcción, procesos de Markov . Para distribuciones generales del tamaño de paso, satisfaciendo la condición de potencia, la distancia desde el origen de la caminata aleatoria tiende, después de un gran número de pasos, a una distribución estable debido al teorema del límite central generalizado , lo que permite que muchos procesos modelarse utilizando vuelos de Lévy.

Las densidades de probabilidad de las partículas que experimentan un vuelo de Levy se pueden modelar utilizando una versión generalizada de la ecuación de Fokker-Planck , que generalmente se usa para modelar el movimiento browniano . La ecuación requiere el uso de derivadas fraccionarias . Para longitudes de salto que tienen una distribución de probabilidad simétrica, la ecuación toma una forma simple en términos de la derivada fraccionaria de Riesz . En una dimensión, la ecuación se lee como

Figura 1. Un ejemplo de 1000 pasos de un vuelo Lévy en dos dimensiones. El origen del movimiento está en [0,0], la dirección angular se distribuye uniformemente y el tamaño del paso se distribuye de acuerdo con una distribución de Lévy (es decir, estable ) con α  = 1 y β  = 0, que es una distribución de Cauchy . Tenga en cuenta la presencia de grandes saltos en la ubicación en comparación con el movimiento browniano ilustrado en la Figura 2.

Figura 2. Un ejemplo de 1000 pasos de una aproximación a un tipo de movimiento browniano de vuelo de Lévy en dos dimensiones. El origen del movimiento está en [0, 0], la dirección angular se distribuye uniformemente y el tamaño del paso se distribuye según una distribución de Lévy (es decir, estable ) con α  = 2 y β  = 0 ( es decir, una distribución normal ).