Onda de Poisson

En matemáticas, en el análisis funcional, varias ondas diferentes se conocen con el nombre de ondas de Poisson . En un contexto, el término "ondícula de Poisson" se utiliza para denotar una familia de ondículas etiquetadas por el conjunto de números enteros positivos , cuyos miembros están asociados con la distribución de probabilidad de Poisson . Estas ondas fueron definidas y estudiadas por primera vez por Karlene A. Kosanovich, Allan R. Moser y Michael J. Piovoso en 1995-1996. ^{[1] [2]} En otro contexto, el término se refiere a una cierta ondícula que involucra una forma del núcleo integral de Poisson. ^[3]En otro contexto más, la terminología se usa para describir una familia de ondículas complejas indexadas por enteros positivos que están conectados con las derivadas del núcleo integral de Poisson. ^[4]

Ondas asociadas con la distribución de probabilidad de Poisson

Definición

Los miembros de la familia de Poisson wavelets que corresponde a n = 1, 2, 3, 4.

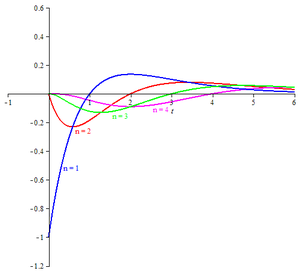
Para cada entero positivo n, la ondícula de Poisson se define por${\displaystyle \psi _{n}(t)}$

${\displaystyle \psi _{n}(t)={\begin{cases}\left({\frac {t-n}{n!}}\right)t^{n-1}e^{-t}&{\text{ for }}t\geq 0\\0&{\text{ for }}t<0.\end{cases}}}$

Para ver la relación entre la ondícula de Poisson y la distribución de Poisson, sea X una variable aleatoria discreta que tenga la distribución de Poisson con el parámetro (media) t y, para cada entero no negativo n , sea Prob ( X = n ) = p _n ( t ). Entonces nosotros tenemos

${\displaystyle p_{n}(t)={\frac {t^{n}}{n!}}e^{-t}.}$

La ondícula de Poisson ahora está dada por${\displaystyle \psi _{n}(t)}$

${\displaystyle \psi _{n}(t)=-{\frac {d}{dt}}p_{n}(t).}$

Propiedades básicas

• ${\displaystyle \psi _{n}(t)}$ es la diferencia hacia atrás de los valores de la distribución de Poisson:

${\displaystyle \psi _{n}(t)=p_{n}(t)-p_{n-1}(t).}$

• La "ondulación" de los miembros de esta familia de ondículas se deriva de

${\displaystyle \int _{-\infty }^{\infty }\psi _{n}(t)\,dt=0.}$

• La transformada de Fourier se da${\displaystyle \psi _{n}(t)}$

${\displaystyle \Psi (\omega )={\frac {-i\omega }{(1+i\omega )^{n+1}}}.}$

• La constante de admisibilidad asociada con es${\displaystyle \psi _{n}(t)}$

${\displaystyle C_{\psi _{n}}=\int _{-\infty }^{\infty }{\frac {\left|\Psi _{n}(\omega )\right|^{2}}{|\omega |}}\,d\omega ={\frac {1}{n}}.}$

• La ondícula de Poisson no es una familia ortogonal de ondículas.

Transformada de ondas de Poisson

La familia de ondas de Poisson se puede utilizar para construir la familia de transformadas de funciones de ondas de Poisson definidas en el dominio del tiempo. Dado que las ondas de Poisson también satisfacen la condición de admisibilidad, las funciones en el dominio del tiempo se pueden reconstruir a partir de sus transformadas de ondas de Poisson utilizando la fórmula para las transformadas de ondas de tiempo continuo inversas.

Si f ( t ) es una función en el dominio del tiempo, su n -ésima transformada de ondas de Poisson está dada por

${\displaystyle (W_{n}f)(a,b)={\frac {1}{\sqrt {|a|}}}\int _{-\infty }^{\infty }f(t)\psi _{n}\left({\frac {t-b}{a}}\right)\,dt}$

En la dirección inversa, dada la n -ésima transformada de ondas de Poisson de una función f ( t ) en el dominio del tiempo, la función f ( t ) se puede reconstruir de la siguiente manera:${\displaystyle (W_{n}f)(a,b)}$

${\displaystyle f(t)={\frac {1}{C_{\psi _{n}}}}\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }\,\left\{(W_{n}f)(a,b){\frac {1}{\sqrt {|a|}}}\psi _{n}\left({\frac {t-b}{a}}\right)\,\right\}db\right]{\frac {da}{a^{2}}}}$

Aplicaciones

Las transformadas de ondas de Poisson se han aplicado en análisis de múltiples resoluciones, identificación de sistemas y estimación de parámetros. Son particularmente útiles para estudiar problemas en los que las funciones en el dominio del tiempo consisten en combinaciones lineales de exponenciales decrecientes con retardo de tiempo.

Wavelet asociado con el núcleo de Poisson

Imagen de la ondícula asociada al kernel de Poisson.

Imagen de la transformada de Fourier de la ondícula asociada al núcleo de Poisson.

Definición

La ondícula de Poisson está definida por la función ^[3]

${\displaystyle \psi (t)={\frac {1}{\pi }}{\frac {1-t^{2}}{(1+t^{2})^{2}}}}$

Esto se puede expresar en la forma

${\displaystyle \psi (t)=P(t)+t{\frac {d}{dt}}P(t)}$donde .${\displaystyle P(t)={\frac {1}{\pi }}{\frac {1}{1+t^{2}}}}$

Relación con el kernel de Poisson

La función aparece como un núcleo integral en la solución de un cierto problema de valor inicial del operador de Laplace .${\displaystyle P(t)}$

Este es el problema del valor inicial: dado cualquier en , encuentre una función armónica definida en el semiplano superior que satisfaga las siguientes condiciones:${\displaystyle s(x)}$${\displaystyle L^{p}(\mathbb {R} )}$${\displaystyle \phi (x,y)}$

1. ${\displaystyle \int _{-\infty }^{\infty }|\phi (x,y)|^{p}\,dx\leq c<\infty }$, y
2. ${\displaystyle \phi (x,y)\rightarrow s(x)}$como en .${\displaystyle y\rightarrow 0}$${\displaystyle L^{p}(\mathbb {R} )}$

El problema tiene la siguiente solución: hay exactamente una función que satisface las dos condiciones y está dada por${\displaystyle \phi (x,y)}$

${\displaystyle \phi (t,y)=P_{y}(t)\star s(t)}$

donde y donde " " denota la operación de convolución . La función es el núcleo integral de la función . La función es la continuación armónica de en el semiplano superior.${\displaystyle P_{y}(t)={\frac {1}{y}}P\left({\frac {t}{y}}\right)={\frac {1}{\pi }}{\frac {y}{t^{2}+y^{2}}}}$${\displaystyle \star }$${\displaystyle P_{y}(t)}$${\displaystyle \phi (x,y)}$${\displaystyle \phi (x,y)}$${\displaystyle s(x)}$

Propiedades

• La "ondulación" de la función se deriva de

${\displaystyle \int _{-\infty }^{\infty }\psi (t)\,dt=0}$.

• La transformada de Fourier de está dada por${\displaystyle \psi (t)}$

${\displaystyle \Psi (\omega )=|\omega |e^{-|\omega |}}$.

• La constante de admisibilidad es

${\displaystyle C_{\psi }=\int _{-\infty }^{\infty }{\frac {\left|\Psi (\omega )\right|^{2}}{|\omega |}}\,d\omega =2.}$

Una clase de ondículas complejas asociadas con el núcleo de Poisson

Las gráficas de las partes reales de la ondícula de Poisson para .${\displaystyle \psi _{n}(t)}$${\displaystyle n=1,2,3,4}$

Las gráficas de las partes imaginarias de la ondícula de Poisson para .${\displaystyle \psi _{n}(t)}$${\displaystyle n=1,2,3,4}$

Definición

La ondícula de Poisson es una familia de funciones con valores complejos indexadas por el conjunto de números enteros positivos y definidas por ^{[4] [5]}

${\displaystyle \psi _{n}(t)={\frac {1}{2\pi }}(1-it)^{-(n+1)}}$ dónde ${\displaystyle n=1,2,3,\ldots }$

Relación con el kernel de Poisson

La función se puede expresar como una n -ésima derivada de la siguiente manera:${\displaystyle \psi _{n}(t)}$

${\displaystyle \psi _{n}(t)={\frac {1}{2\pi }}{\frac {1}{n!\,i^{n}}}{\frac {d^{n}}{dt^{n}}}\left((1-it)^{-1}\right)}$

Escribiendo la función en términos del núcleo integral de Poisson como ${\displaystyle (1-it)^{-1}}$${\displaystyle P(t)={\frac {1}{1+t^{2}}}}$

${\displaystyle (1-it)^{-1}=P(t)+itP(t)}$

tenemos

${\displaystyle \psi _{n}(t)={\frac {1}{2\pi }}{\frac {1}{n!\,i^{n}}}{\frac {d^{n}}{dt^{n}}}P(t)+i\left({\frac {1}{2\pi }}{\frac {1}{n!\,i^{n}}}{\frac {d^{n}}{dt^{n}}}\left(tP(t)\right)\right)}$

Por tanto, se puede interpretar como una función proporcional a las derivadas del núcleo integral de Poisson.${\displaystyle \psi _{n}(t)}$

Propiedades

La transformada de Fourier de está dada por${\displaystyle \psi _{n}(t)}$

${\displaystyle \Psi _{n}(\omega )={\frac {1}{\Gamma (n+1)}}\omega ^{n}e^{-\omega }u(\omega )}$

donde es la función de paso unitario .${\displaystyle u(\omega )}$

Referencias

1. Karlene A. Kosanovich, Allan R. Moser y Michael J. Piovoso (1996). "La transformada de ondas de Poisson". Comunicaciones de ingeniería química . 146 (1): 131-138.
2. Karlene A. Kosanovich, Allan R. Moser y Michael J. Piovoso (1997). "Una nueva familia de wavelets: la transformada de wavelets de Poisson". Computadoras en Ingeniería Química . 21 (6): 601–620.
3. Roland Klees, Roger Haagmans (editores) (2000). Wavelets en las Geociencias . Berlín: Springer. págs. 18-20.
4. Abdul J. Jerri (1998). El fenómeno de Gibbs en análisis de Fourier, splines y aproximaciones wavelet . Dordrech: Springer Science + Business Media. págs.  222 –224. ISBN 978-1-4419-4800-7.
5. Wojbor A. Woyczynski (1997). Distribuciones en las Ciencias Físicas y de la Ingeniería: Cálculo de Distribución y Fractal, Transformaciones Integrales y Ondas, Volumen 1 . Springer Science & Business Media. pag. 223. ISBN 9780817639242.