Proporción de población

Parámetros que denotan fracciones de poblaciones, generalmente como porcentaje

En estadística , una proporción de la población , generalmente denotada por${\displaystyle P}$o la letra griega ${\displaystyle \pi }$, ^{[1] [2]} es un parámetro que describe un valor porcentual asociado con una población . Por ejemplo, el censo de los Estados Unidos de 2010 mostró que el 83,7% de la población estadounidense se identificó como no hispana o latina; el valor de .837 es una proporción de población. En general, se desconocen la proporción de la población y otros parámetros de la población. Se puede realizar un censo para determinar el valor real de un parámetro de población, pero a menudo un censo no es práctico debido a sus costos y consumo de tiempo.

Una proporción de la población generalmente se estima a través de una muestra estadística no sesgada obtenida de un estudio o experimento observacional . Por ejemplo, la Conferencia Nacional de Alfabetización Tecnológica realizó una encuesta nacional de 2.000 adultos para determinar el porcentaje de adultos que son analfabetos económicos. El estudio mostró que el 72% de los 2.000 adultos incluidos en la muestra no entendían qué es un producto interno bruto . ^[3] El valor del 72% es una proporción de muestra. La proporción de la muestra generalmente se denota por${\displaystyle {\hat {p}}}$ y en algunos libros de texto por ${\displaystyle p}$. ^{[1] [4] [5]}

Definición matemática

Una ilustración del diagrama de Venn de un conjunto ${\displaystyle R}$ y su subconjunto ${\displaystyle S}$. La proporción se puede calcular midiendo la cantidad de${\displaystyle S}$ es en ${\displaystyle R}$.

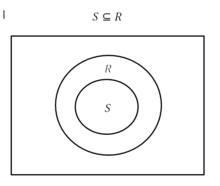
Una proporción se define matemáticamente como la relación de los valores en un subconjunto${\displaystyle S}$ a los valores en un conjunto ${\displaystyle R}$.

Como tal, la proporción de la población se puede definir de la siguiente manera:

${\displaystyle P={\frac {X}{N}}}$ (donde ${\displaystyle X}$ es el recuento de éxitos en la población, y ${\displaystyle N}$ es el tamaño de la población)

Esta definición matemática se puede generalizar para proporcionar la definición de la proporción muestral:

${\displaystyle {\hat {p}}={\frac {x}{n}}}$ (donde ${\displaystyle x}$ es el recuento de éxitos en la muestra, y ${\displaystyle n}$es el tamaño de la muestra obtenida de la población) ^{[6] [4]}

Estimación

Uno de los principales focos de estudio de la estadística inferencial es determinar el valor "verdadero" de un parámetro. Generalmente, el valor real de un parámetro nunca se encontrará, a menos que se realice un censo de la población de estudio. Sin embargo, existen métodos estadísticos que se pueden utilizar para obtener una estimación razonable de un parámetro. Estos métodos incluyen intervalos de confianza y pruebas de hipótesis .

Estimar el valor de una proporción de la población puede tener una gran implicación en las áreas de agricultura , negocios , economía , educación , ingeniería , estudios ambientales , medicina , derecho , ciencias políticas , psicología y sociología .

Se puede estimar una proporción de población mediante el uso de un intervalo de confianza conocido como proporción de una muestra en el intervalo Z, cuya fórmula se da a continuación:

${\displaystyle {\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}$ (donde ${\displaystyle {\hat {p}}}$ es la proporción de la muestra, ${\displaystyle n}$ es el tamaño de la muestra, y ${\displaystyle z^{*}}$ es el superior ${\displaystyle {\frac {1-C}{2}}}$ valor crítico de la distribución normal estándar para un nivel de confianza${\displaystyle C}$) ^[7]

Prueba

Para derivar la fórmula para la proporción de una muestra en el intervalo Z , se debe tener en cuenta una distribución muestral de las proporciones muestrales. La media de la distribución muestral de las proporciones muestrales generalmente se denota como${\displaystyle \mu _{\hat {p}}=P}$ y su desviación estándar se denota como ${\displaystyle \sigma _{\hat {p}}={\sqrt {\frac {P(1-P)}{n}}}}$. ^[4] Dado que el valor de${\displaystyle P}$ es desconocido, una estadística imparcial ${\displaystyle {\hat {p}}}$ será utilizado para ${\displaystyle P}$. La media y la desviación estándar se reescriben como${\displaystyle \mu _{\hat {p}}={\hat {p}}}$ y ${\displaystyle \sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}$respectivamente. Invocando el teorema del límite central , la distribución muestral de las proporciones muestrales es aproximadamente normal, siempre que la muestra sea razonablemente grande y no esté sesgada.

Suponga que se calcula la siguiente probabilidad: ${\displaystyle P(-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*})=C}$, donde ${\displaystyle 0<C<1}$ y ${\displaystyle \pm z^{*}}$ son los valores críticos estándar.

La distribución muestral de las proporciones muestrales es aproximadamente normal cuando satisface los requisitos del Teorema del límite central.

La desigualdad ${\displaystyle -z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}}$ se puede reescribir algebraicamente de la siguiente manera:

${\displaystyle -z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}\Rightarrow -z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}<{\hat {p}}-P<z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}\Rightarrow -{\hat {p}}-z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}<-P<-{\hat {p}}+z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}\Rightarrow {\hat {p}}-z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}<P<{\hat {p}}+z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}$A partir del trabajo algebraico realizado anteriormente, es evidente desde un nivel de certeza ${\displaystyle C}$ ese${\displaystyle P}$ podría caer entre los valores de ${\displaystyle {\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}$.

Condiciones para la inferencia

En general, la fórmula utilizada para estimar una proporción de población requiere sustituciones de valores numéricos conocidos. Sin embargo, estos valores numéricos no se pueden sustituir "ciegamente" en la fórmula porque la inferencia estadística requiere que la estimación de un parámetro desconocido sea justificable. Para que la estimación de un parámetro sea justificable, hay tres condiciones que deben verificarse:

1. La observación individual de los datos debe obtenerse de una muestra aleatoria simple de la población de interés.
2. Las observaciones individuales de los datos deben mostrar normalidad . Esto se puede verificar matemáticamente con la siguiente definición:
   • Dejar ${\displaystyle n}$ ser el tamaño de muestra de una muestra aleatoria dada y dejar ${\displaystyle {\hat {p}}}$sea ​​su proporción muestral. Si ${\displaystyle n{\hat {p}}\geq 10}$ y ${\displaystyle n(1-{\hat {p}})\geq 10}$, entonces las observaciones individuales de los datos muestran normalidad.
3. Las observaciones individuales de los datos deben ser independientes entre sí. Esto se puede verificar matemáticamente con la siguiente definición:
   • Dejar ${\displaystyle N}$ ser el tamaño de la población de interés y dejar ${\displaystyle n}$ser el tamaño de la muestra de una muestra aleatoria simple de la población. Si${\displaystyle N\geq 10n}$, entonces las observaciones individuales de los datos son independientes entre sí.

Las condiciones para el SRS, la normalidad y la independencia a veces se denominan condiciones para la caja de herramientas de inferencia en la mayoría de los libros de texto estadísticos.

Ejemplo

Supongamos que se llevan a cabo elecciones presidenciales en una democracia. Una muestra aleatoria de 400 votantes elegibles en la población de votantes de la democracia muestra que 272 votantes apoyan al candidato B. Un científico político quiere determinar qué porcentaje de la población de votantes apoya al candidato B.

Para responder a la pregunta del politólogo, se puede construir una proporción de una muestra en el intervalo Z con un nivel de confianza del 95% para determinar la proporción de la población de votantes elegibles en esta democracia que apoyan al candidato B.

Solución

Se sabe a partir de la muestra aleatoria que ${\displaystyle {\hat {p}}={\frac {272}{400}}=0.68}$ con tamaño de muestra ${\displaystyle n=400}$. Antes de construir un intervalo de confianza, se verificarán las condiciones para la inferencia.

• Dado que se obtuvo una muestra aleatoria de 400 votantes de la población votante, se ha cumplido la condición de una muestra aleatoria simple.
• Dejar ${\displaystyle n=400}$ y ${\displaystyle {\hat {p}}=0.68}$, se comprobará si ${\displaystyle n{\hat {p}}\geq 10}$ y ${\displaystyle n(1-{\hat {p}})\geq 10}$

${\displaystyle (400)(0.68)\geq 10\Rightarrow 272\geq 10}$ y ${\displaystyle (400)(1-0.68)\geq 10\Rightarrow 128\geq 10}$

Se ha cumplido la condición de normalidad.

• Dejar ${\displaystyle N}$ ser el tamaño de la población de votantes en esta democracia, y dejar ${\displaystyle n=400}$. Si${\displaystyle N\geq 10n}$, luego está la independencia.

${\displaystyle N\geq 10(400)\Rightarrow N\geq 4000}$

El tamaño de la población ${\displaystyle N}$pues se puede suponer que los votantes de esta democracia son al menos 4.000. Por tanto, se ha cumplido la condición de independencia.

Con las condiciones para la inferencia verificadas, es permisible construir un intervalo de confianza.

Dejar ${\displaystyle {\hat {p}}=0.68,n=400,}$ y ${\displaystyle C=0.95}$

Para resolver ${\displaystyle z^{*}}$, la expresión ${\displaystyle {\frac {1-C}{2}}}$ se utiliza.

${\displaystyle {\frac {1-C}{2}}={\frac {1-0.95}{2}}={\frac {0.05}{2}}=0.0250}$

La curva normal estándar con ${\displaystyle z^{*}}$ lo que da un área de cola superior de 0.0250 y un área de 0.9750 para ${\displaystyle Z\leq z^{*}}$.

Una tabla con probabilidades normales estándar para ${\displaystyle Z\leq z}$.

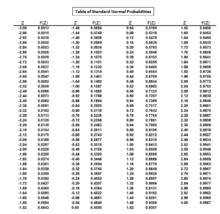
Al examinar una curva de campana normal estándar, el valor de ${\displaystyle z^{*}}$se puede determinar identificando qué puntuación estándar le da a la curva normal estándar un área de cola superior de 0.0250 o un área de 1 - 0.0250 = 0.9750. El valor de${\displaystyle z^{*}}$ también se puede encontrar a través de una tabla de probabilidades normales estándar.

De una tabla de probabilidades normales estándar, el valor de ${\displaystyle Z}$que da un área de 0.9750 es 1.96. Por tanto, el valor de${\displaystyle z^{*}}$ es 1,96.

Los valores para ${\displaystyle {\hat {p}}=0.68}$, ${\displaystyle n=400}$, ${\displaystyle z^{*}=1.96}$ ahora se puede sustituir en la fórmula para la proporción de una muestra en el intervalo Z:

${\displaystyle {\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}\Rightarrow (0.68)\pm (1.96){\sqrt {\frac {(0.68)(1-0.68)}{(400)}}}\Rightarrow 0.68\pm 1.96{\sqrt {0.000544}}}$ ${\displaystyle \Rightarrow {\bigl (}0.63429,0.72571{\bigr )}}$

Con base en las condiciones de inferencia y la fórmula para la proporción de una muestra en el intervalo Z, se puede concluir con un nivel de confianza del 95% que el porcentaje de la población de votantes en esta democracia que apoya al candidato B está entre 63,429% y 72,571 %.

Valor del parámetro en el rango del intervalo de confianza

Una pregunta común en la estadística inferencial es si el parámetro se incluye dentro de un intervalo de confianza. La única forma de responder a esta pregunta es realizar un censo. Con referencia al ejemplo anterior, la probabilidad de que la proporción de la población esté en el rango del intervalo de confianza es 1 o 0. Es decir, el parámetro está incluido en el rango del intervalo o no. El propósito principal de un intervalo de confianza es ilustrar mejor cuál podría ser el valor ideal para un parámetro.

Errores comunes y malas interpretaciones de la estimación

Un error muy común que surge de la construcción de un intervalo de confianza es la creencia de que el nivel de confianza, como ${\displaystyle C=95\%}$, significa 95% de probabilidad. Esto es incorrecto. El nivel de confianza se basa en una medida de certeza, no de probabilidad. Por tanto, los valores de${\displaystyle C}$ caen entre 0 y 1, exclusivamente.

Ver también

• Intervalo de confianza de la proporción binomial
• Intervalo de confianza
• Predominio
• Prueba de hipótesis estadística
• Inferencia estadística
• Parámetro estadístico
• Intervalo de tolerancia

Referencias

1. "Lista de símbolos de probabilidad y estadística" . Bóveda de matemáticas . 2020-04-26 . Consultado el 22 de agosto de 2020 .
2. Introducción a las investigaciones estadísticas . Wiley. ISBN 978-1-118-95667-0.
3. Ott, R. Lyman. Introducción a los métodos estadísticos y al análisis de datos . ISBN 0-534-93150-2.
4. Weisstein, Eric W. "Proporción de la muestra" . mathworld.wolfram.com . Consultado el 22 de agosto de 2020 .
5. "6.3: La proporción de la muestra" . Estadísticas LibreTexts . 2014-04-16 . Consultado el 22 de agosto de 2020 .
6. Weisstein, Eric. Enciclopedia Concisa de Matemáticas CRC . Chapman y Hall / CRC.
7. Obstáculos, Duane. Edición anotada del profesor La práctica de la estadística . ISBN 0-7167-7703-7.