Secuencia de baja discrepancia
En matemáticas , una secuencia de discrepancia baja es una secuencia con la propiedad de que para todos los valores de N , su subsecuencia x 1 , ..., x N tiene una discrepancia baja .
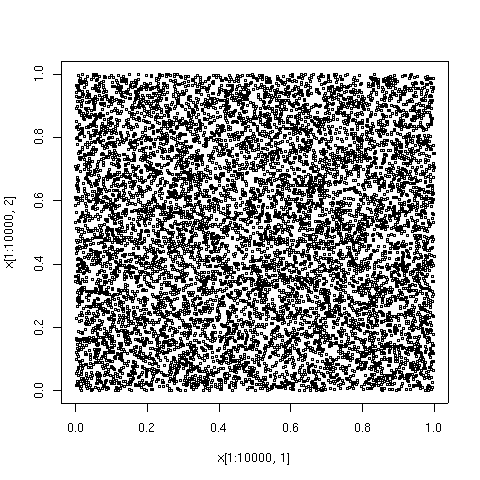
En términos generales, la discrepancia de una secuencia es baja si la proporción de puntos en la secuencia que caen en un conjunto arbitrario B es casi proporcional a la medida de B , como sucedería en promedio (pero no para muestras particulares) en el caso de una secuencia equidistribuida . Las definiciones específicas de discrepancia difieren con respecto a la elección de B ( hiperesferas , hipercubos, etc.) y cómo la discrepancia para cada B se calcula (generalmente normalizada) y se combina (generalmente tomando el peor valor).
Las secuencias de baja discrepancia también se denominan secuencias cuasialeatorias , debido a su uso común como reemplazo de números aleatorios distribuidos uniformemente . El modificador "cuasi" se usa para indicar más claramente que los valores de una secuencia de discrepancia baja no son ni aleatorios ni pseudoaleatorios , pero tales secuencias comparten algunas propiedades de variables aleatorias y en ciertas aplicaciones, como el método cuasi-Monte Carlo, su discrepancia más baja . es una ventaja importante.
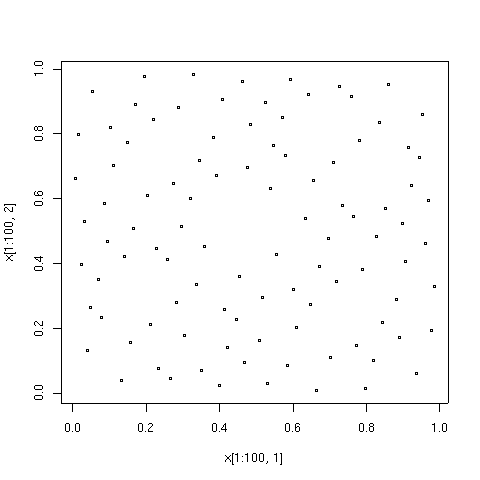
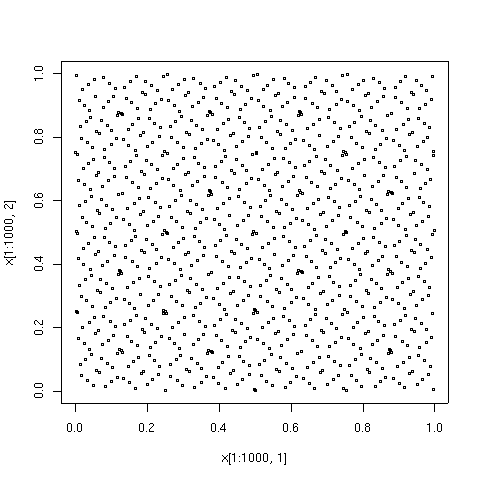
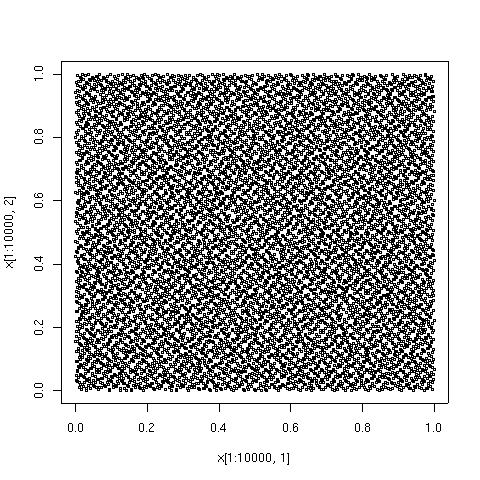
Los números cuasialeatorios tienen una ventaja sobre los números aleatorios puros porque cubren el dominio de interés de manera rápida y uniforme. Tienen una ventaja sobre los métodos puramente deterministas en que los métodos deterministas solo brindan alta precisión cuando el número de puntos de datos está preestablecido, mientras que al usar secuencias cuasialeatorias, la precisión generalmente mejora continuamente a medida que se agregan más puntos de datos, con la reutilización completa de los puntos existentes. Por otro lado, los conjuntos de puntos cuasialeatorios pueden tener una discrepancia significativamente menor para un número determinado de puntos que las secuencias puramente aleatorias.
Dos aplicaciones útiles son encontrar la función característica de una función de densidad de probabilidad y encontrar la función derivada de una función determinista con una pequeña cantidad de ruido. Los números cuasialeatorios permiten calcular momentos de orden superior con gran precisión con mucha rapidez.
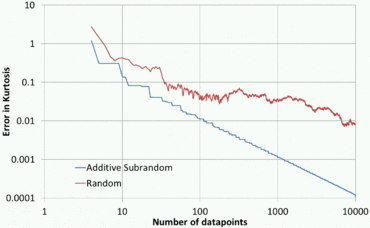
Las aplicaciones que no implican ordenamiento serían encontrar la media , la desviación estándar , la asimetría y la curtosis de una distribución estadística, y encontrar los máximos y mínimos integrales y globales de funciones deterministas difíciles. Los números cuasialeatorios también se pueden utilizar para proporcionar puntos de partida para algoritmos deterministas que solo funcionan localmente, como la iteración Newton-Raphson .