Mapa autoorganizado
Un mapa autoorganizado ( SOM ) o un mapa de características autoorganizado ( SOFM ) es una técnica de aprendizaje automático no supervisada que se utiliza para producir una representación de baja dimensión (normalmente bidimensional) de un conjunto de datos de mayor dimensión, al tiempo que se preserva la estructura topológica del datos. Por ejemplo, un conjunto de datos con p variables medidas en nlas observaciones podrían representarse como grupos de observaciones con valores similares para las variables. Estos grupos luego podrían visualizarse como un "mapa" bidimensional de modo que las observaciones en los grupos proximales tengan valores más similares que las observaciones en los grupos distales. Esto puede hacer que los datos de alta dimensión sean más fáciles de visualizar y analizar.
Un SOM es un tipo de red neuronal artificial, pero se entrena mediante aprendizaje competitivo en lugar del aprendizaje de corrección de errores (p. ej., propagación inversa con descenso de gradiente ) utilizado por otras redes neuronales artificiales. El SOM fue presentado por el profesor finlandés Teuvo Kohonen en la década de 1980 y, por lo tanto, a veces se lo denomina mapa de Kohonen o red de Kohonen . [1] [2] El mapa o red de Kohonen es una abstracción computacionalmente conveniente basada en modelos biológicos de sistemas neuronales de la década de 1970 [3] y modelos de morfogénesis que se remontan aAlan Turing en la década de 1950. [4]
Los mapas autoorganizados, como la mayoría de las redes neuronales artificiales, funcionan de dos modos: entrenamiento y mapeo. En primer lugar, el entrenamiento utiliza un conjunto de datos de entrada (el "espacio de entrada") para generar una representación de menor dimensión de los datos de entrada (el "espacio de mapa"). En segundo lugar, el mapeo clasifica los datos de entrada adicionales utilizando el mapa generado.
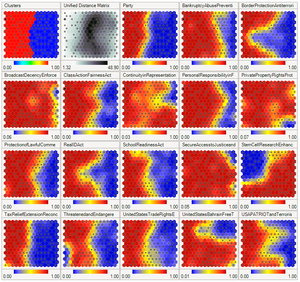
En la mayoría de los casos, el objetivo del entrenamiento es representar un espacio de entrada con p dimensiones como un espacio de mapa con dos dimensiones. Específicamente, se dice que un espacio de entrada con p variables tiene p dimensiones. Un espacio de mapa consta de componentes llamados "nodos" o "neuronas", que están dispuestos como una cuadrícula hexagonal o rectangular con dos dimensiones. [5] El número de nodos y su disposición se especifican de antemano en función de los objetivos más amplios del análisis y exploración de los datos .
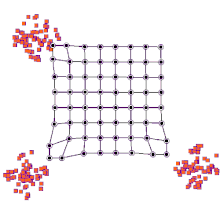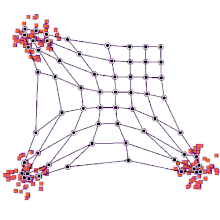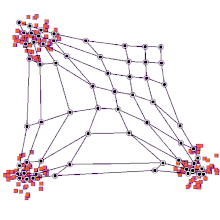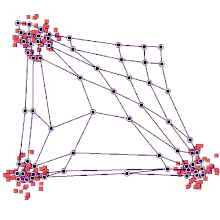
Cada nodo en el espacio del mapa está asociado con un vector de "peso", que es la posición del nodo en el espacio de entrada. Si bien los nodos en el espacio del mapa permanecen fijos, el entrenamiento consiste en mover los vectores de peso hacia los datos de entrada (reduciendo una métrica de distancia como la distancia euclidiana ) sin estropear la topología inducida desde el espacio del mapa. Después del entrenamiento, el mapa se puede usar para clasificar observaciones adicionales para el espacio de entrada al encontrar el nodo con el vector de peso más cercano (métrica de distancia más pequeña) al vector espacial de entrada.
El objetivo del aprendizaje en el mapa autoorganizado es hacer que diferentes partes de la red respondan de manera similar a ciertos patrones de entrada. Esto se debe en parte a cómo se maneja la información visual, auditiva u otra información sensorial en partes separadas de la corteza cerebral en el cerebro humano . [6]