En el análisis complejo, el fenómeno de Stokes , descubierto por GG Stokes ( 1847 , 1858 ), es que el comportamiento asintótico de las funciones puede diferir en diferentes regiones del plano complejo. Estas regiones están delimitadas por la línea Stokes o las líneas anti-Stokes .
Líneas de Stokes y líneas anti-Stokes
De manera algo confusa, los matemáticos y físicos usan los términos "línea de Stokes" y "línea anti-Stokes" de manera opuesta. Las líneas originalmente estudiadas por Stokes son lo que algunos matemáticos llaman líneas anti-Stokes y lo que los físicos llaman líneas de Stokes. (Estos términos también se utilizan en óptica para las líneas de Stokes no relacionadas y las líneas anti-Stokes en la dispersión Raman ). Este artículo utiliza la convención de los físicos, que históricamente es más precisa y parece volverse más común entre los matemáticos. Olver (1997) recomienda el término "curva principal" para las líneas anti-Stokes (del físico).
De manera informal, las líneas anti-Stokes son aproximadamente donde algún término en la expansión asintótica cambia de creciente a decreciente (y por lo tanto puede exhibir un comportamiento puramente oscilatorio), y las líneas de Stokes son líneas a lo largo de las cuales algún término se acerca al infinito o cero más rápidamente. Las líneas anti-Stokes limitan regiones donde la función exhibe un comportamiento asintótico particular. Las líneas de Stokes y las líneas anti-Stokes no son únicas y realmente no tienen una definición precisa en general, porque la región donde una función tiene un comportamiento asintótico dado es un concepto algo vago. Sin embargo, las líneas suelen tener direcciones bien determinadas en las singularidades esenciales de la función y, a veces, hay una elección natural de estas líneas de la siguiente manera. La expansión asintótica de una función suele estar dada por una combinación lineal de funciones de la formaf ( z ) e ± g ( z ) para las funciones f y g . Las líneas de Stokes pueden entonces tomarse como los ceros de la parte imaginaria de g , y las líneas anti-Stokes como los ceros de la parte real de g . (Esto no es del todo canónico, porque se puede agregar una constante ag , cambiando las líneas). Si las líneas se definen así, entonces son ortogonales donde se encuentran, a menos que g tenga un cero múltiple.
Como ejemplo trivial, la función sinh ( z ) tiene dos regiones Re ( z )> 0 y Re ( z ) <0 donde es asintótica con e z / 2 y −e - z / 2. Entonces, la línea anti-Stokes puede tomarse como el eje imaginario y la línea de Stokes como el eje real. Se podría igualmente tomar la línea de Stokes como cualquier línea de una parte imaginaria dada; estas opciones difieren solo por un cambio vertical, lo que demuestra que no existe una opción canónica para la línea de Stokes.
Ejemplo: la función Airy
La función de Airy Ai ( x ) es una de dos soluciones a una ecuación diferencial simple
que a menudo es útil aproximar para muchos valores de x , incluidos los valores complejos. Para x grande de un argumento dado, la solución se puede aproximar mediante una combinación lineal de las funciones
Sin embargo, la combinación lineal tiene que cambiar a medida que el argumento de x pasa ciertos valores porque estas aproximaciones son funciones de varios valores, pero la función de Airy es de un solo valor. Por ejemplo, si consideramos que el límite de x es grande y real, y nos gustaría aproximar la función de Airy tanto para valores positivos como negativos, encontraríamos que

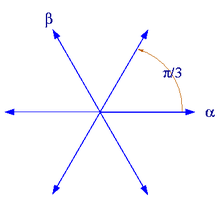
que son dos expresiones muy diferentes. Lo que ha sucedido es que a medida que aumentamos el argumento de x de 0 a pi (rotándolo a través del semiplano complejo superior) hemos cruzado una línea anti-Stokes, que en este caso está en. En esta línea anti-Stokes, el coeficiente dese ve obligado a saltar. El coeficiente depuede saltar en esta línea pero no está obligado a hacerlo; puede cambiar gradualmente a medida que arg x varía de π / 3 a π, ya que no está determinado en esta región.
Hay tres líneas anti-Stokes con argumentos π / 3, π. –Π / 3 y tres líneas de Stokes con argumentos 2π / 3, 0. –2π / 3.
Ejemplo: ecuaciones diferenciales lineales de segundo orden
El ejemplo de la función de Airy se puede generalizar a una amplia clase de ecuaciones diferenciales lineales de segundo orden de la siguiente manera. Mediante cambios estándar de variables, una ecuación de segundo orden a menudo se puede cambiar a una de la forma
donde f es holomorfa en una región simplemente conectada y w es una solución de la ecuación diferencial. Entonces, en algunos casos, el método WKB da una aproximación asintótica para w como una combinación lineal de funciones de la forma
por alguna constante a . (Elegir diferentes valores de a es equivalente a elegir diferentes coeficientes en la combinación lineal.) Las líneas anti-Stokes y las líneas de Stokes son los ceros de las partes real e imaginaria, respectivamente, de
Si a es un simple cero de f , localmente f se ve como. Las soluciones se comportarán localmente como las funciones de Airy; tendrán tres líneas Stokes y tres líneas anti-Stokes que se reunirán en a .
Ver también
Referencias
- Berry, MV (1988), "Fenómeno de Stokes; suavizando una discontinuidad victoriana". , Inst. Hautes Études Sci. Publ. Matemáticas. , 68 : 211–221, doi : 10.1007 / bf02698550 , MR 1001456 , S2CID 121293430
- Berry, MV (1989), "Suavizado asintótico uniforme de las discontinuidades de Stokes", Proc. Roy. Soc. Lond. A , 422 (1862): 7–21, Bibcode : 1989RSPSA.422 .... 7B , doi : 10.1098 / rspa.1989.0018 , JSTOR 2398522 , MR 0990851 , S2CID 122020328
- Meyer, RE (1989), "Una explicación simple del fenómeno de Stokes" , SIAM Rev. , 31 (3): 435–445, doi : 10.1137 / 1031090 , JSTOR 2031404 , MR 1012299
- Olver, Frank William John (1997) [1974], Asintótica y funciones especiales , AKP Classics, Wellesley, MA: AK Peters Ltd., ISBN 978-1-56881-069-0, Señor 1429619
- Stokes, GG (1847), "Sobre el cálculo numérico de una clase de integrales definidas y series infinitas" , Transactions of the Cambridge Philosophical Society , IX (I): 166-189
- Stokes, GG (1858), "Sobre la discontinuidad de constantes arbitrarias que aparecen en desarrollos divergentes" , Transactions of the Cambridge Philosophical Society , X (I): 105-128
- Witten, Ed (2010). "Continuación analítica de la teoría de Chern-Simons". arXiv : 1001,2933v4 [ hep-ésimo ].
- Bender, Carl M. (1978), Métodos matemáticos avanzados para científicos e ingenieros , Serie internacional en matemáticas puras y aplicadas, McGraw Hill Inc., ISBN 0-07-004452-X
- Ablowitz, MJ y Fokas, AS (2003). Variables complejas: introducción y aplicaciones. Prensa de la Universidad de Cambridge .









