Número complejo

En matemáticas , un número complejo es un elemento de un sistema numérico que contiene los números reales y un elemento específico denotado i , llamado unidad imaginaria , y que satisface la ecuación i ² = −1 . Además, cada número complejo se puede expresar en la forma a + bi , donde a y b son números reales. Como ningún número real satisface la ecuación anterior, René Descartes me llamó un número imaginario . Para el número complejo a+ bi , a se llamala parte real ybsellamaparte imaginaria . El conjunto denúmeros complejos se indica mediante los símboloso C. A pesar de la nomenclatura histórica "imaginaria", los números complejos se consideran en lasciencias matemáticastan "reales" como los números reales y son fundamentales en muchos aspectos de la descripción científica del mundo natural. ^{[1] [a]}${\ Displaystyle \ mathbb {C}}$

Los números complejos permiten soluciones para todas las ecuaciones polinomiales , incluso aquellas que no tienen soluciones en números reales. Más precisamente, el teorema fundamental del álgebra afirma que toda ecuación polinomial no constante con coeficientes reales o complejos tiene una solución que es un número complejo. Por ejemplo, la ecuación no tiene solución real, ya que el cuadrado de un número real no puede ser negativo, pero tiene las dos soluciones complejas no reales −1 + 3 i y −1 - 3 i .${\ Displaystyle (x + 1) ^ {2} = - 9}$

La suma, resta y multiplicación de números complejos se pueden definir naturalmente usando la regla i ² = −1 combinada con las leyes asociativas , conmutativas y distributivas . Todo número complejo distinto de cero tiene un inverso multiplicativo . Esto hace que los números complejos sean un campo que tiene los números reales como subcampo. Los números complejos también forman un espacio vectorial real de dimensión dos, con {1, i } como base estándar .

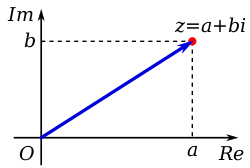
Esta base estándar hace que los números complejos sean un plano cartesiano , llamado plano complejo . Esto permite una interpretación geométrica de los números complejos y sus operaciones y, a la inversa, expresar en términos de números complejos algunas propiedades y construcciones geométricas. Por ejemplo, los números reales forman la línea real que se identifica con el eje horizontal del plano complejo. Los números complejos de valor absoluto uno forman el círculo unitario . La suma de un número complejo es una traslación en el plano complejo, y la multiplicación por un número complejo es una similitud centrada en el origen. La conjugación compleja es lasimetría de reflexión con respecto al eje real. El valor absoluto complejo es una norma euclidiana .

En resumen, los números complejos forman una estructura rica que es simultáneamente un campo algebraicamente cerrado , un álgebra conmutativa sobre los reales y un espacio vectorial euclidiano de dimensión dos.

Un número complejo es un número de la forma a + bi , donde ayb son números reales e i es un número indeterminado que satisface i ² = −1 . Por ejemplo, 2 + 3 i es un número complejo. ^[3]

Un número complejo se puede representar visualmente como un par de números ( a ,  b ) que forman un vector en un diagrama llamado diagrama de Argand , que representa el plano complejo . Re es el eje real, Im es el eje imaginario e i es la " unidad imaginaria ", que satisface i ² = −1 .

Una ilustración del número complejo z = x + iy en el plano complejo . La parte real es x y su parte imaginaria es y .

Un número complejo z , como un punto (negro) y su vector de posición (azul)

El argumento φ y el módulo r ubican un punto en el plano complejo.

Un gráfico de rueda de color de la expresión ( z ² - 1) ( z - 2 - i ) ² / z ² + 2 + 2 i

Representación geométrica de zy su conjugado z en el plano complejo

La suma de dos números complejos se puede hacer geométricamente construyendo un paralelogramo.

Multiplicación de 2 + i (triángulo azul) y 3 + i (triángulo rojo). El triángulo rojo se gira para que coincida con el vértice del azul (la suma de ambos ángulos en los términos φ ₁ + φ ₂ en la ecuación) y se estira por la longitud de la hipotenusa del triángulo azul (la multiplicación de ambos radios, según el término r ₁ r ₂ en la ecuación).

Representación geométrica de la segunda a la sexta raíces de un número complejo z , en forma polar re ^iφ  donde r = | z  | y φ = arg z . Si z es real, φ = 0 o π . Las raíces principales se muestran en negro.

Gráfico de rueda de color de sin (1 / z ) . Las partes negras en el interior se refieren a números que tienen valores absolutos grandes.

El conjunto de Mandelbrot con los ejes real e imaginario etiquetados.

Construcción de un pentágono regular usando regla y compás .

Gráfico de cuaterniones Cayley Q8 que muestra los ciclos de multiplicación por i , j y k