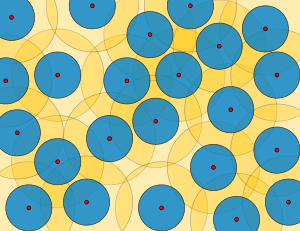
Conjunto de Delone
En la teoría matemática de los espacios métricos , las redes ε , las empaquetaduras ε , las cubiertas ε , los conjuntos uniformemente discretos , los conjuntos relativamente densos y los conjuntos Delone (nombrados en honor a Boris Delone ) son varias definiciones estrechamente relacionadas de conjuntos de puntos bien espaciados, y el radio de empaque y el radio de cobertura de estos conjuntos miden qué tan bien espaciados están. Estos conjuntos tienen aplicaciones en la teoría de la codificación , los algoritmos de aproximación y la teoría de los cuasicristales .
Si ( M , d ) es un espacio métrico, y X es un subconjunto de M , entonces el radio de embalaje de X es la mitad de la infimum de distancias entre los miembros distintos de X . Si el radio de empaquetadura es r , entonces las bolas abiertas de radio r centradas en los puntos de X serán todas disjuntas entre sí, y cada bola abierta centrada en uno de los puntos de X con radio 2 r estará disjunta del resto de X . El radio de cobertura de X es el mínimo de los números.r tal que cada punto de M está dentro de la distancia r de al menos un punto en X ; es decir, es el radio más pequeño tal que bolas cerradas de ese radio centradas en los puntos de X tienen todo M como su unión. Un ε -cajones es un conjunto X de embalaje radio ≥ ε / 2 (equivalentemente, distancia mínima ≥ ε), un ε-recubrimiento es un conjunto X de cubrir radio ≤ ε , y un ε-net es un conjunto que es a la vez una Embalaje ε y una cubierta ε . Un conjunto es uniformemente discretosi tiene un radio de empaquetamiento distinto de cero, y relativamente denso si tiene un radio de cobertura finito. Un conjunto de Delone es un conjunto uniformemente discreto y relativamente denso; por lo tanto, cada ε -net es Delone, pero no al revés. [1] [2]
Como la más restrictiva de las definiciones anteriores, las redes ε son al menos tan difíciles de construir como las empaquetaduras ε, las cubiertas ε y los conjuntos Delone. Sin embargo, siempre que los puntos de M tienen un buen orden , la inducción transfinita muestra que es posible construir un ε-net N , incluyendo en N todos los puntos para los cuales el mínimo de distancias al conjunto de puntos anteriores en el orden es al menos ε. Para conjuntos finitos de puntos en un espacio euclidiano de dimensión acotada, cada punto puede probarse en tiempo constante mapeándolo a una cuadrícula de celdas de diámetro ε, y usando una tabla hash para probar qué celdas cercanas ya contienen puntos de N; por tanto, en este caso, se puede construir una red ε en tiempo lineal . [3] [4]
Para espacios métricos finitos o compactos más generales, se puede utilizar un algoritmo alternativo de Teo González basado en el primer recorrido más lejano para construir una red ε finita. Este algoritmo se inicializa la red N a estar vacío, y después se añade varias veces para N el punto más lejano de M de N , rompiendo los lazos de forma arbitraria y deteniéndose cuando todos los puntos de M están a distancia de ε N . [5] En espacios de dimensión de duplicación acotada , el algoritmo de González se puede implementar en O ( n log n) tiempo para conjuntos de puntos con una relación polinomial entre sus distancias más lejanas y más cercanas, y aproximado en el mismo tiempo limitado para conjuntos de puntos arbitrarios. [6]
En la teoría de los códigos de corrección de errores , el espacio métrico que contiene un código de bloque C consta de cadenas de una longitud fija, digamos n , tomadas sobre un alfabeto de tamaño q (puede considerarse como vectores ), con la métrica de Hamming . Este espacio se denota con . El radio de cobertura y el radio de empaque de este espacio métrico están relacionados con la capacidad del código para corregir errores.
Har-Peled & Raichel (2013) describen un paradigma algorítmico que ellos llaman "net and podar" para diseñar algoritmos de aproximación para ciertos tipos de problemas de optimización geométrica definidos en conjuntos de puntos en espacios euclidianos . Un algoritmo de este tipo funciona realizando los siguientes pasos: