regresión lineal

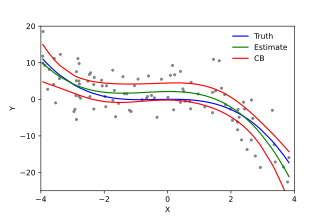
En estadística , la regresión lineal es un enfoque lineal para modelar la relación entre una respuesta escalar y una o más variables explicativas (también conocidas como variables dependientes e independientes ). El caso de una variable explicativa se denomina regresión lineal simple ; para más de uno, el proceso se denomina regresión lineal múltiple . [1] Este término es distinto de la regresión lineal multivariante , donde se predicen múltiples variables dependientes correlacionadas , en lugar de una única variable escalar. [2]

En la regresión lineal, las relaciones se modelan mediante funciones predictoras lineales cuyos parámetros desconocidos del modelo se estiman a partir de los datos . Estos modelos se denominan modelos lineales . [3] Más comúnmente, se supone que la media condicional de la respuesta dados los valores de las variables explicativas (o predictores) es una función afín de esos valores; con menos frecuencia, se utiliza la mediana condicional o algún otro cuantil . Como todas las formas de análisis de regresión , la regresión lineal se centra en la distribución de probabilidad condicionalde la respuesta dados los valores de los predictores, en lugar de la distribución de probabilidad conjunta de todas estas variables, que es el dominio del análisis multivariante .

La regresión lineal fue el primer tipo de análisis de regresión que se estudió rigurosamente y se usó ampliamente en aplicaciones prácticas. [4] Esto se debe a que los modelos que dependen linealmente de sus parámetros desconocidos son más fáciles de ajustar que los modelos que no están relacionados linealmente con sus parámetros y porque las propiedades estadísticas de los estimadores resultantes son más fáciles de determinar.

La regresión lineal tiene muchos usos prácticos. La mayoría de las aplicaciones se incluyen en una de las siguientes dos amplias categorías:

Los modelos de regresión lineal a menudo se ajustan utilizando el enfoque de mínimos cuadrados , pero también se pueden ajustar de otras maneras, como minimizando la "falta de ajuste" en alguna otra norma (como con la regresión de mínimas desviaciones absolutas ), o minimizando una penalización. versión de la función de costo de mínimos cuadrados como en la regresión de cresta ( L 2 - penalización de norma) y lazo ( L 1 - penalización de norma). Por el contrario, el enfoque de mínimos cuadrados se puede utilizar para ajustar modelos que no son modelos lineales. Así, aunque los términos "mínimos cuadrados" y "modelo lineal" están estrechamente vinculados, no son sinónimos.

Dado un conjunto de datos de n unidades estadísticas , un modelo de regresión lineal asume que la relación entre la variable dependiente y y el vector p de regresores x es lineal . Esta relación se modela a través de un término de perturbación o variable de error ε , una variable aleatoria no observada que agrega "ruido" a la relación lineal entre la variable dependiente y los regresores. Así el modelo toma la forma

En la regresión lineal, se supone que las observaciones ( rojo ) son el resultado de desviaciones aleatorias ( verde ) de una relación subyacente ( azul ) entre una variable dependiente ( y ) y una variable independiente ( x ).
Ejemplo de una regresión polinomial cúbica, que es un tipo de regresión lineal. Aunque la regresión polinomial ajusta un modelo no lineal a los datos, como problema de estimación estadística es lineal, en el sentido de que la función de regresión E( y | x ) es lineal en los parámetros desconocidos que se estiman a partir de los datos . Por esta razón, la regresión polinomial se considera un caso especial de regresión lineal múltiple .
Para verificar las violaciones de las suposiciones de linealidad, varianza constante e independencia de errores dentro de un modelo de regresión lineal, los residuos generalmente se grafican contra los valores pronosticados (o cada uno de los predictores individuales). Una dispersión aparentemente aleatoria de puntos alrededor de la línea media horizontal en 0 es ideal, pero no puede descartar ciertos tipos de violaciones como la autocorrelación en los errores o su correlación con una o más covariables.
Los conjuntos de datos del cuarteto de Anscombe están diseñados para tener aproximadamente la misma línea de regresión lineal (así como medias, desviaciones estándar y correlaciones casi idénticas), pero gráficamente son muy diferentes. Esto ilustra los peligros de confiar únicamente en un modelo ajustado para comprender la relación entre las variables.
Ejemplo de regresión lineal simple , que tiene una variable independiente
Ilustración de Francis Galton de 1886 [12] de la correlación entre las alturas de los adultos y sus padres. La observación de que la altura de los hijos adultos tendía a desviarse menos de la altura media que la de sus padres sugirió el concepto de " regresión hacia la media ", dando a la regresión su nombre. El "lugar geométrico de los puntos tangenciales horizontales" que pasan por los puntos más a la izquierda y más a la derecha de la elipse (que es una curva de nivel de la distribución normal bivariada estimada a partir de los datos) es el MCOestimación de la regresión de las alturas de los padres sobre las alturas de los hijos, mientras que el "lugar geométrico de los puntos tangenciales verticales" es la estimación MCO de la regresión de las alturas de los niños sobre las alturas de los padres. El eje principal de la elipse es la estimación de TLS .
Comparación del estimador de Theil-Sen (negro) y la regresión lineal simple (azul) para un conjunto de puntos con valores atípicos.