teorema del valor medio

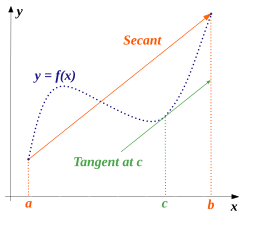
En matemáticas , el teorema del valor medio establece, aproximadamente, que para un arco plano dado entre dos extremos, hay al menos un punto en el que la tangente al arco es paralela a la secante que pasa por sus extremos. Es uno de los resultados más importantes en el análisis real . Este teorema se utiliza para probar enunciados sobre una función en un intervalo a partir de hipótesis locales sobre derivadas en puntos del intervalo.

Más precisamente, el teorema establece que si es una función continua en el intervalo cerrado y diferenciable en el intervalo abierto , entonces existe un punto en el que la tangente en es paralela a la secante que pasa por los extremos y , es decir,${\ estilo de visualización f}$ ${\ estilo de visualización [a, b]}$ ${\ estilo de visualización (a, b)}$${\ estilo de visualización c}$${\ estilo de visualización (a, b)}$${\ estilo de visualización c}$${\displaystyle {\grande (}a,f(a){\grande)}}$${\displaystyle {\grande (}b,f(b){\grande)}}$

Un caso especial de este teorema fue descrito por primera vez por Parameshvara (1380-1460), de la Escuela de Astronomía y Matemáticas de Kerala en la India , en sus comentarios sobre Govindasvāmi y Bhāskara II . ^[1] Michel Rolle demostró una forma restringida del teorema en 1691; el resultado fue lo que ahora se conoce como el teorema de Rolle , y se demostró solo para polinomios, sin las técnicas del cálculo. El teorema del valor medio en su forma moderna fue enunciado y demostrado por Augustin Louis Cauchy en 1823. ^[2] Desde entonces se han demostrado muchas variaciones de este teorema.^{[3] [4]}

Sea una función continua en el intervalo cerrado , y derivable en el intervalo abierto , donde . Entonces existe algo en tal que${\displaystyle f:[a,b]\to \mathbb {R} }$ ${\ estilo de visualización [a, b]}$${\ estilo de visualización (a, b)}$${\ estilo de visualización a <b}$${\ estilo de visualización c}$${\ estilo de visualización (a, b)}$

El teorema del valor medio es una generalización del teorema de Rolle , que supone , de modo que el lado derecho de arriba es cero.${\ estilo de visualización f (a) = f (b)}$

El teorema del valor medio sigue siendo válido en un entorno un poco más general. Solo se necesita asumir que es continuo en , y que para todo en el límite${\displaystyle f:[a,b]\to \mathbb {R} }$${\ estilo de visualización [a, b]}$${\ estilo de visualización x}$${\ estilo de visualización (a, b)}$

Para cualquier función que es continua en y derivable en existe alguna en el intervalo tal que la secante que une los extremos del intervalo es paralela a la tangente en .${\ estilo de visualización [a, b]}$${\ estilo de visualización (a, b)}$${\ estilo de visualización c}$${\ estilo de visualización (a, b)}$${\ estilo de visualización [a, b]}$${\ estilo de visualización c}$

La función obtiene la pendiente de la secante entre y como derivada en el punto .${\ estilo de visualización f}$${\ estilo de visualización a}$${\ estilo de visualización b}$${\ estilo de visualización \ xi \ en (a, b)}$

También es posible que haya múltiples tangentes paralelas a la secante.

Significado geométrico del teorema de Cauchy

Geométricamente: interpretando f(c) como la altura de un rectángulo y b – a como el ancho, este rectángulo tiene la misma área que la región debajo de la curva de a a b ^[11]