Método de diferencias finitas
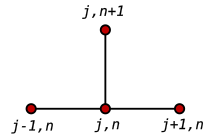
En análisis numérico , los métodos de diferencias finitas ( FDM ) son una clase de técnicas numéricas para resolver ecuaciones diferenciales mediante la aproximación de derivadas con diferencias finitas . Tanto el dominio espacial como el intervalo de tiempo (si corresponde) están discretizados o divididos en un número finito de pasos, y el valor de la solución en estos puntos discretos se aproxima resolviendo ecuaciones algebraicas que contienen diferencias finitas y valores de puntos cercanos.
Los métodos de diferencias finitas convierten las ecuaciones diferenciales ordinarias (EDO) o las ecuaciones diferenciales parciales (PDE), que pueden ser no lineales , en un sistema de ecuaciones lineales que pueden resolverse mediante técnicas de álgebra matricial. Las computadoras modernas pueden realizar estos cálculos de álgebra lineal de manera eficiente, lo que, junto con su relativa facilidad de implementación, ha llevado al uso generalizado de FDM en el análisis numérico moderno. [1] Hoy en día, FDM es uno de los enfoques más comunes para la solución numérica de PDE, junto con los métodos de elementos finitos . [1]
Primero, suponiendo que la función cuyas derivadas deben aproximarse se comporta correctamente, según el teorema de Taylor , podemos crear una expansión en serie de Taylor
donde n ! denota el factorial de n , y R n ( x ) es un término restante, que denota la diferencia entre el polinomio de Taylor de grado n y la función original. Derivaremos una aproximación para la primera derivada de la función "f" truncando primero el polinomio de Taylor:
Suponiendo que sea suficientemente pequeño, la aproximación de la primera derivada de "f" es:
El error en la solución de un método se define como la diferencia entre la aproximación y la solución analítica exacta. Las dos fuentes de error en los métodos de diferencias finitas son el error de redondeo, la pérdida de precisión debido al redondeo de cantidades decimales por computadora y el error de truncamiento o error de discretización , la diferencia entre la solución exacta de la ecuación diferencial original y la cantidad exacta asumiendo aritmética perfecta (es decir, asumiendo que no hay redondeo).