Centripetal force

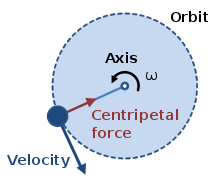
A centripetal force (from Latin centrum, "center" and petere, "to seek"[1]) is a force that makes a body follow a curved path. Its direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre".[2] In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

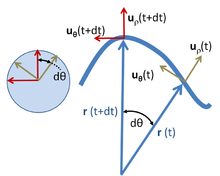
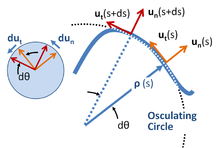
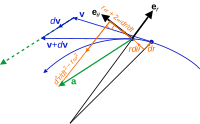
One common example involving centripetal force is the case in which a body moves with uniform speed along a circular path. The centripetal force is directed at right angles to the motion and also along the radius towards the centre of the circular path.[3][4] The mathematical description was derived in 1659 by the Dutch physicist Christiaan Huygens.[5]

The magnitude of the centripetal force on an object of mass m moving at tangential speed v along a path with radius of curvature r is:[6]

In particle accelerators, velocity can be very high (close to the speed of light in vacuum) so the same rest mass now exerts greater inertia (relativistic mass) thereby requiring greater force for the same centripetal acceleration, so the equation becomes:[10]

In the case of an object that is swinging around on the end of a rope in a horizontal plane, the centripetal force on the object is supplied by the tension of the rope. The rope example is an example involving a 'pull' force. The centripetal force can also be supplied as a 'push' force, such as in the case where the normal reaction of a wall supplies the centripetal force for a wall of death or a Rotor rider.

Newton's idea of a centripetal force corresponds to what is nowadays referred to as a central force. When a satellite is in orbit around a planet, gravity is considered to be a centripetal force even though in the case of eccentric orbits, the gravitational force is directed towards the focus, and not towards the instantaneous center of curvature.[11]

A body experiencing uniform circular motion requires a centripetal force, towards the axis as shown, to maintain its circular path.
Vector relationships for uniform circular motion; vector Ω representing the rotation is normal to the plane of the orbit with polarity determined by the right-hand rule and magnitude dθ /dt.
Upper panel: Ball on a banked circular track moving with constant speed v; Lower panel: Forces on the ball
/ R.
Velocity vector v, always tangent to the path of motion.
Acceleration vector a, not parallel to the radial motion but offset by the angular and Coriolis accelerations, nor tangent to the path but offset by the centripetal and radial accelerations.
Kinematic vectors in plane polar coordinates. Notice the setup is not restricted to 2d space, but a plane in any higher dimension.
Polar unit vectors at two times t and t + dt for a particle with trajectory r ( t ); on the left the unit vectors uρ and uθ at the two times are moved so their tails all meet, and are shown to trace an arc of a unit radius circle. Their rotation in time dt is dθ, just the same angle as the rotation of the trajectory r ( t ).
Local coordinate system for planar motion on a curve. Two different positions are shown for distances s and s + ds along the curve. At each position s, unit vector un points along the outward normal to the curve and unit vector ut is tangential to the path. The radius of curvature of the path is ρ as found from the rate of rotation of the tangent to the curve with respect to arc length, and is the radius of the osculating circle at position s. The unit circle on the left shows the rotation of the unit vectors with s.