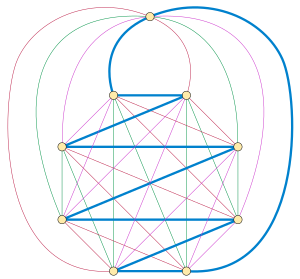
Descomposición hamiltoniana

Descomposición hamiltoniana de Walecki del gráfico completo ${\displaystyle K_{9}}$

En la teoría de grafos , una rama de las matemáticas, una descomposición hamiltoniana de un gráfico dado es una partición de los bordes del gráfico en ciclos hamiltonianos . Las descomposiciones hamiltonianas se han estudiado tanto para gráficos no dirigidos como para gráficos dirigidos . En el caso no dirigido, una descomposición hamiltoniana también se puede describir como una factorización en 2 del gráfico de modo que cada factor esté conectado.

Condiciones necesarias

Para que exista una descomposición hamiltoniana en un gráfico no dirigido, el gráfico debe estar conectado y ser regular de grado par . Un gráfico dirigido con tal descomposición debe estar fuertemente conectado y todos los vértices deben tener el mismo grado de entrada y de salida que los demás, pero este grado no necesita ser uniforme. ^[1]

El gráfico medial del gráfico de Herschel es un gráfico plano regular de 4 sin descomposición hamiltoniana. Las regiones sombreadas corresponden a los vértices del gráfico Herschel subyacente.

Para grafos planos regulares de 4 , se pueden derivar condiciones adicionales necesarias del teorema de Grinberg . Un ejemplo de un gráfico plano de 4 regulares que no cumple estas condiciones y no tiene una descomposición hamiltoniana lo da el gráfico medial del gráfico de Herschel . ^[2]

Gráficos completos

Todo gráfico completo con un número impar de vértices tiene una descomposición hamiltoniana. Este resultado, que es un caso especial del problema de Oberwolfach de descomponer grafos completos en 2 factores isomorfos, fue atribuido a Walecki por Édouard Lucas en 1892. La construcción de Walecki coloca los vértices en un polígono regular y cubre el grafo completo en este subconjunto de vértices con rutas hamiltonianas que zigzaguean a través del polígono, con cada ruta rotada entre sí por un múltiplo de . Luego, todos los caminos se pueden completar a ciclos hamiltonianos conectando sus extremos a través del vértice restante. ^[3]${\displaystyle n}$${\displaystyle n-1}$${\displaystyle (n-1)/2}$${\displaystyle \pi /(n-1)}$

La expansión de un vértice de un gráfico regular en un grupo de vértices, uno para cada punto final de una arista en el vértice reemplazado, no puede cambiar si el gráfico tiene una descomposición hamiltoniana. Lo contrario de este proceso de expansión, colapsando una camarilla en un solo vértice, transformará cualquier descomposición hamiltoniana en el gráfico más grande en una descomposición hamiltoniana en el gráfico original. Por el contrario, la construcción de Walecki se puede aplicar a la camarilla para expandir cualquier descomposición hamiltoniana del gráfico más pequeño en una descomposición hamiltoniana del gráfico expandido. Este proceso de expansión se puede utilizar para producir arbitrariamente grandes gráficos de vértice-transitivo y grafos de Cayley de grado incluso que no tienen descomposiciones de Hamilton.${\displaystyle 2k}$${\displaystyle 2k}$^[4]

El caso dirigido de gráficos completos son los torneos . Respondiendo a una conjetura de Paul Kelly de 1968, ^[5] Daniela Kühn y Deryk Osthus demostraron en 2012 que todo torneo regular suficientemente grande tiene una descomposición hamiltoniana. ^[6]

Número de descomposiciones

Cada grafo no dirigido de 4 regulares tiene un número par de descomposiciones hamiltonianas. Más fuertemente, por cada dos aristas y de un gráfico de 4 regulares, el número de descomposiciones hamiltonianas en las que y pertenecen al mismo ciclo es par. Si un gráfico -regular tiene una descomposición hamiltoniana, tiene al menos un número factorial triple de descomposiciones,${\displaystyle e}$${\displaystyle f}$${\displaystyle e}$${\displaystyle f}$${\displaystyle 2k}$

${\displaystyle (3k-2)\cdot (3k-5)\cdots 7\cdot 4\cdot 1.}$

Por ejemplo, los gráficos 4-regulares que tienen una descomposición hamiltoniana tienen al menos cuatro de ellos; Las gráficas 6-regulares que tienen una descomposición hamiltoniana tienen al menos 28, etc. De ello se deduce que las únicas gráficas cuyas descomposiciones hamiltonianas son únicas son las gráficas de ciclo . ^[7]

Complejidad computacional

Probar si un gráfico arbitrario tiene una descomposición hamiltoniana es NP-completo , tanto en los casos dirigidos como no dirigidos. ^[8] En particular, la pregunta es NP-completa para gráficos regulares de un grado par especificado; por ejemplo, para gráficos de 4 regulares.

Los gráficos lineales de los gráficos cúbicos son 4-regulares y tienen una descomposición hamiltoniana si y solo si el gráfico cúbico subyacente tiene un ciclo hamiltoniano. ^{[9] [10]} Como consecuencia, la descomposición hamiltoniana sigue siendo NP-completa para las clases de gráficos que incluyen gráficos lineales de instancias concretas del problema del ciclo hamiltoniano . Por ejemplo, la descomposición hamiltoniana es NP-completa para las gráficas planas de 4 regulares, porque incluyen las gráficas lineales de las gráficas planas cúbicas. Por otro lado, esta equivalencia también implica que la descomposición hamiltoniana es fácil para gráficos de 4 líneas regulares cuando sus gráficos cúbicos subyacentes tienen problemas sencillos de ciclo hamiltoniano.

Es casi seguro que los gráficos regulares aleatorios de grado par tengan una descomposición hamiltoniana, y más fuertemente existe un algoritmo de tiempo polinomial aleatorio que, cuando se le da como entrada un gráfico regular aleatorio de grado par, casi seguramente encuentra una descomposición hamiltoniana en él. ^[11]

Ver también

• Arboricidad lineal , un tipo diferente de partición restringida en subgrafos de máximo grado dos

Referencias

1. Bermond, J.-C. (1978), "Descomposiciones hamiltonianas de gráficos, gráficos dirigidos e hipergráficos" , Annals of Discrete Mathematics , 3 : 21-28 , doi : 10.1016 / S0167-5060 (08) 70494-1 , ISBN 9780720408430, MR  0505807
2. Bondy, JA ; Häggkvist, R. (1981), "Ciclos de Hamilton con bordes disjuntos en gráficas planas de 4 regulares", Aequationes Mathematicae , 22 (1): 42–45, doi : 10.1007 / BF02190157 , MR 0623315 
3. Alspach, Brian (2008), "La maravillosa construcción de Walecki", Boletín del Instituto de Combinatoria y sus Aplicaciones , 52 : 7-20, MR 2394738 
4. Bryant, Darryn; Dean, Matthew (2015), "Gráficos transitivos de vértice que no tienen descomposición de Hamilton", Journal of Combinatorial Theory, Serie B , 114 : 237–246, doi : 10.1016 / j.jctb.2015.05.007 , MR 3354297 
5. Moon, John W. (1968), Temas sobre torneos , Nueva York, Montreal, Londres: Holt, Rinehart y Winston, Ejercicio 9, página 9, MR 0256919 
6. Kühn, Daniela ; Osthus, Deryk (2013), "Descomposiciones de Hamilton de expansores regulares: una prueba de la conjetura de Kelly para torneos grandes", Advances in Mathematics , 237 : 62-146, arXiv : 1202.6219 , doi : 10.1016 / j.aim.2013.01.005 , Señor 3028574 
7. Thomason, AG (1978), "Ciclos hamiltonianos y gráficos coloreables de borde único", Avances en la teoría de grafos (Conf. Combinatoria de Cambridge, Trinity College, Cambridge, 1977) , Annals of Discrete Mathematics, 3 , págs. 259-268, MR 0499124 
8. Péroche, B. (1984), "NP-completitud de algunos problemas de partición y cobertura en gráficos", Matemáticas aplicadas discretas , 8 (2): 195-208, doi : 10.1016 / 0166-218X (84) 90101-X , MR 0743024 
9. Kotzig, Anton (1957), "Aus der Theorie der endlichen regulären Graphen dritten und vierten Grades", Časopis Pro Pěstování Matematiky , 82 : 76–92, MR 0090815 
10. Martin, Pierre (1976), "Cycles hamiltoniens dans les graphes 4-réguliers 4-connexes", Aequationes Mathematicae , 14 (1/2): 37–40, doi : 10.1007 / BF01836203 , MR 0414442 
11. Kim, Jeong Han; Wormald, Nicholas C. (2001), "Emparejamientos aleatorios que inducen ciclos de Hamilton y descomposiciones hamiltonianas de gráficos regulares aleatorios", Journal of Combinatorial Theory, Serie B , 81 (1): 20–44, doi : 10.1006 / jctb.2000.1991 , Señor 1809424