Teorema de la monodromía

Ilustración de la continuación analítica a lo largo de una curva (solo se muestra un número finito de discos ).${\displaystyle U_{t}}$

Continuación analítica a lo largo de una curva del logaritmo natural (solo se muestra la parte imaginaria del logaritmo).

En el análisis complejo , el teorema de la monodromía es un resultado importante sobre la continuación analítica de una función analítica compleja a un conjunto mayor. La idea es que se puede extender una función analítica compleja (de aquí en adelante llamada simplemente función analítica ) a lo largo de curvas que comienzan en el dominio original de la función y terminan en el conjunto más grande. Un problema potencial de esta continuación analítica a lo largo de una curvaLa estrategia es que generalmente hay muchas curvas que terminan en el mismo punto en el conjunto más grande. El teorema de la monodromía proporciona condiciones suficientes para que la continuación analítica dé el mismo valor en un punto dado independientemente de la curva utilizada para llegar allí, de modo que la función analítica ampliada resultante esté bien definida y de un solo valor.

Antes de enunciar este teorema es necesario definir la continuación analítica a lo largo de una curva y estudiar sus propiedades.

Continuación analítica a lo largo de una curva

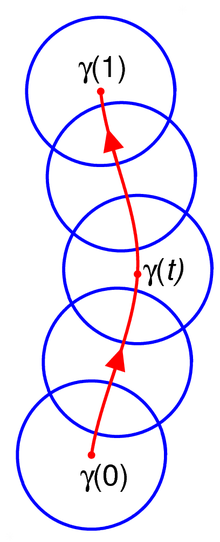
La definición de continuación analítica a lo largo de una curva es un poco técnica, pero la idea básica es que se comienza con una función analítica definida alrededor de un punto y se extiende esa función a lo largo de una curva a través de funciones analíticas definidas en pequeños discos superpuestos que cubren esa curva.

Formalmente, considere una curva (una función continua ) Sea una función analítica definida en un disco abierto centrado en Una continuación analítica del par a lo largo es una colección de pares para que${\displaystyle \gamma :[0,1]\to \mathbb {C} .}$${\displaystyle f}$ ${\displaystyle U}$${\displaystyle \gamma (0).}$${\displaystyle (f,U)}$${\displaystyle \gamma }$${\displaystyle (f_{t},U_{t})}$${\displaystyle 0\leq t\leq 1}$

• ${\displaystyle f_{0}=f}$ y ${\displaystyle U_{0}=U.}$

• Porque cada uno es un disco abierto centrado en y es una función analítica.${\displaystyle t\in [0,1],U_{t}}$${\displaystyle \gamma (t)}$${\displaystyle f_{t}:U_{t}\to \mathbb {C} }$

• Para cada existe tal que para todos con uno tiene eso (lo que implica que y tiene una intersección no vacía ) y las funciones y coinciden en la intersección${\displaystyle t\in [0,1]}$${\displaystyle \varepsilon >0}$${\displaystyle t'\in [0,1]}$${\displaystyle |t-t'|<\varepsilon }$${\displaystyle \gamma (t')\in U_{t}}$${\displaystyle U_{t}}$${\displaystyle U_{t'}}$${\displaystyle f_{t}}$${\displaystyle f_{t'}}$${\displaystyle U_{t}\cap U_{t'}.}$

Propiedades de la continuación analítica a lo largo de una curva

Continuación analítica a lo largo de una curva es esencialmente único, en el sentido de que da dos extensión analítica y de a lo largo de las funciones y coinciden en Informalmente, esto dice que dos continuaciones analíticas de a lo largo de terminarán con los mismos valores en un barrio de${\displaystyle (f_{t},U_{t})}$${\displaystyle (g_{t},V_{t})}$ ${\displaystyle (0\leq t\leq 1)}$${\displaystyle (f,U)}$${\displaystyle \gamma ,}$${\displaystyle f_{1}}$${\displaystyle g_{1}}$${\displaystyle U_{1}\cap V_{1}.}$${\displaystyle (f,U)}$${\displaystyle \gamma }$${\displaystyle \gamma (1).}$

Si la curva es cerrada (es decir, ), no es necesario tener igual en una vecindad de Por ejemplo, si se comienza en un punto con y el logaritmo complejo definido en una vecindad de este punto, y uno deja ser el círculo de radio centrado en el origen (viajado en sentido antihorario desde ), luego, al hacer una continuación analítica a lo largo de esta curva, se obtendrá un valor del logaritmo en el que es más el valor original (ver la segunda ilustración a la derecha). ${\displaystyle \gamma }$${\displaystyle \gamma (0)=\gamma (1)}$${\displaystyle f_{0}}$${\displaystyle f_{1}}$${\displaystyle \gamma (0).}$${\displaystyle (a,0)}$${\displaystyle a>0}$${\displaystyle \gamma }$${\displaystyle a}$${\displaystyle (a,0)}$${\displaystyle (a,0)}$${\displaystyle 2\pi i}$

Teorema de la monodromía

La homotopía con endopuntos fijos es necesaria para que se mantenga el teorema de la monodromía.

Como se señaló anteriormente, dos continuaciones analíticas a lo largo de la misma curva producen el mismo resultado en el punto final de la curva. Sin embargo, dadas dos curvas diferentes que se ramifican desde el mismo punto alrededor del cual se define una función analítica, con las curvas reconectadas al final, no es cierto en general que las continuaciones analíticas de esa función a lo largo de las dos curvas den el mismo valor. en su punto final común.

De hecho, se puede considerar, como en la sección anterior, el logaritmo complejo definido en una vecindad de un punto y el círculo centrado en el origen y el radio.Entonces , es posible viajar de a de dos maneras, en sentido antihorario, en la mitad superior. -arco plano de este círculo, y en el sentido de las agujas del reloj, en el arco semiplano inferior. Los valores del logaritmo a obtenidos por la continuación analítica a lo largo de estos dos arcos diferirán en${\displaystyle (a,0)}$${\displaystyle a.}$${\displaystyle (a,0)}$${\displaystyle (-a,0)}$${\displaystyle (-a,0)}$${\displaystyle 2\pi i.}$

Sin embargo, si uno puede deformar continuamente una de las curvas en otra mientras se mantienen fijos los puntos de inicio y finalización, y es posible la continuación analítica en cada una de las curvas intermedias, entonces las continuaciones analíticas a lo largo de las dos curvas producirán los mismos resultados en su punto final común. Esto se llama teorema de la monodromía y su enunciado se explica con precisión a continuación.

Sea un disco abierto en el plano complejo centrado en un punto y sea ​​una función analítica compleja. Sea otro punto en el plano complejo. Si existe una familia de curvas con tal que y para todas la función es continua, y para cada una es posible hacer una continuación analítica de a lo largo, entonces las continuaciones analíticas de a lo largo y darán los mismos valores en${\displaystyle U}$${\displaystyle P}$${\displaystyle f:U\to \mathbb {C} }$${\displaystyle Q}$${\displaystyle \gamma _{s}:[0,1]\to \mathbb {C} }$${\displaystyle s\in [0,1]}$${\displaystyle \gamma _{s}(0)=P}$${\displaystyle \gamma _{s}(1)=Q}$${\displaystyle s\in [0,1],}$${\displaystyle (s,t)\in [0,1]\times [0,1]\to \gamma _{s}(t)\in \mathbb {C} }$${\displaystyle s\in [0,1]}$${\displaystyle f}$${\displaystyle \gamma _{s},}$${\displaystyle f}$${\displaystyle \gamma _{0}}$${\displaystyle \gamma _{1}}$${\displaystyle Q.}$

El teorema de la monodromía hace posible extender una función analítica a un conjunto mayor a través de curvas que conectan un punto en el dominio original de la función a puntos en el conjunto mayor. El teorema a continuación que establece que también se llama teorema de la monodromía.

Sea un disco abierto en el plano complejo centrado en un punto y sea ​​una función analítica compleja. Si es un conjunto abierto simplemente conectado que contiene y es posible realizar una continuación analítica de sobre cualquier curva contenida en la que comience en, entonces admite una continuación analítica directa para significar que existe una función analítica compleja cuya restricción a es${\displaystyle U}$${\displaystyle P}$${\displaystyle f:U\to \mathbb {C} }$${\displaystyle W}$${\displaystyle U,}$${\displaystyle f}$${\displaystyle W}$${\displaystyle P,}$${\displaystyle f}$${\displaystyle W,}$${\displaystyle g:W\to \mathbb {C} }$${\displaystyle U}$${\displaystyle f.}$

Ver también

• Continuación analítica
• Monodromía

Referencias

• Krantz, Steven G. (1999). Manual de variables complejas . Birkhäuser. ISBN 0-8176-4011-8.
• Jones, Gareth A .; Cantante, David (1987). Funciones complejas: un punto de vista algebraico y geométrico . Prensa de la Universidad de Cambridge. ISBN 0-521-31366-X.

• Triebel, Hans (1986). Análisis y física matemática, ed . Inglesa . D. Reidel Pub. Co. ISBN 90-277-2077-0.

enlaces externos

• Teorema de la monodromía en MathWorld
• Teorema de la monodromía en PlanetMath .
• Teorema de la monodromía en la Enciclopedia de Matemáticas