Grupo de pines

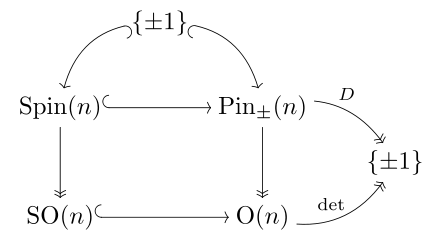
En matemáticas , el grupo de pines es un cierto subgrupo del álgebra de Clifford asociado a un espacio cuadrático . Se asigna 2 a 1 al grupo ortogonal , al igual que el grupo de espín asigna 2 a 1 al grupo ortogonal especial .

En general, el mapa del grupo Pin al grupo ortogonal no es sobre un espacio de cobertura universal , pero si la forma cuadrática es definida (y la dimensión es mayor que 2), es ambos.

Se denota el elemento no trivial del núcleo que no debe confundirse con la transformada ortogonal de reflexión a través del origen , generalmente denotado ${\ Displaystyle \; - 1 ~,}$ ${\ Displaystyle \; - I ~.}$

Definición general

Forma definida

El grupo de clavijas de una forma definida se asigna al grupo ortogonal, y cada componente está simplemente conectado: cubre doblemente el grupo ortogonal. Los grupos de pines para una forma cuadrática definida positiva Q y para su Q negativo no son isomorfos, pero los grupos ortogonales sí lo son. ^{[nota 1]}

En términos de las formas estándar, O ( n , 0) = O (0, n ), pero Pin ( n , 0) y Pin (0, n ) en general no son isomorfos. Usando la convención de signos "+" para álgebras de Clifford (donde ), se escribe ${\ Displaystyle v ^ {2} = Q (v) \ in \ mathrm {Cl} (V, Q)}$

{\ displaystyle {\ mbox {Pin}} _ {+} (n): = {\ mbox {Pin}} (n, 0) \ qquad {\ mbox {Pin}} _ {-} (n): = { \ mbox {Pin}} (0, n)}

y ambos se asignan a O ( n ) = O ( n , 0) = O (0, n ).

Por el contrario, tenemos el isomorfismo natural ^{[nota 2]} Spin ( n , 0) ≅ Spin (0, n ) y ambos son la doble cobertura (única) no trivial del grupo ortogonal especial SO ( n ), que es la (única) cubierta universal para n ≥ 3.

Forma indefinida

Esta sección necesita expansión . Puedes ayudar agregando más . ( Diciembre de 2009 )

Hay hasta ocho cubiertas dobles diferentes de O ( p , q ) , para p , q ≠ 0, que corresponden a las extensiones del centro (que es C ₂ × C ₂ o C ₄ ) por C ₂ . Solo dos de ellos son grupos de pines, los que admiten el álgebra de Clifford como representación. Se llaman Pin ( p , q ) y Pin ( q , p ) respectivamente.

Como grupo topológico

Cada grupo topológico conectado tiene una cobertura universal única como espacio topológico, que tiene una estructura de grupo única como extensión central del grupo fundamental. Para un grupo topológico desconectado, existe una cobertura universal única del componente de identidad del grupo, y uno puede tomar la misma cobertura que los espacios topológicos en los otros componentes (que son espacios homogéneos principales para el componente de identidad) pero la estructura del grupo en otros componentes no se determina de forma única en general.

Los grupos Pin y Spin son grupos topológicos particulares asociados a los grupos ortogonales y ortogonales especiales, provenientes de las álgebras de Clifford: existen otros grupos similares, correspondientes a otras cubiertas dobles oa otras estructuras de grupo en los otros componentes, pero no se refieren a ellos. como grupos Pin o Spin, ni estudié mucho.

En 2001, Andrzej Trautman ^{[nota 3]} encontró el conjunto de las 32 cubiertas dobles no equivalentes de O ( p ) x O ( q ), el subgrupo compacto máximo de O ( p , q ) y una construcción explícita de 8 cubiertas dobles de la mismo grupo O ( p , q ).

Construcción

Los dos grupos de pines corresponden a las dos extensiones centrales

{\ Displaystyle 1 \ to \ {\ pm 1 \} \ to {\ mbox {Pin}} _ {\ pm} (V) \ to \ mathrm {O} (V) \ to 1.}

La estructura del grupo en Spin ( V ) (el componente conectado del determinante 1) ya está determinada; la estructura del grupo en el otro componente está determinada hasta el centro y, por lo tanto, tiene una ambigüedad de ± 1.

Las dos extensiones se distinguen por si la preimagen de una reflexión se cuadra a ± 1 ∈ Ker (Spin ( V ) → SO ( V )), y los dos grupos de pines se nombran en consecuencia. Explícitamente, una reflexión tiene orden 2 en O ( V ), r ² = 1, por lo que el cuadrado de la preimagen de una reflexión (que tiene determinante uno) debe estar en el núcleo de Spin _± ( V ) → SO ( V ), entonces , y cualquiera de las opciones determina un grupo de pines (dado que todas las reflexiones están conjugadas por un elemento de SO ( V ), que está conectado, todas las reflexiones deben cuadrar con el mismo valor). ${\ Displaystyle {\ tilde {r}} ^ {2} = \ pm 1}$

Concretamente, en Pin ₊ , tiene orden 2, y la preimagen de un subgrupo {1, r } es C ₂ × C ₂ : si se repite la misma reflexión dos veces, se obtiene la identidad. ${\ Displaystyle {\ tilde {r}}}$

En Pin _- , tiene orden 4, y la preimagen de un subgrupo {1, r } es C ₄ : si se repite la misma reflexión dos veces, se obtiene "una rotación de 2π", el elemento no trivial de Spin ( V ) → SO ( V ) se puede interpretar como "rotación en 2π" (cada eje produce el mismo elemento). ${\ Displaystyle {\ tilde {r}}}$

Dimensiones reducidas

En 1 dimensión, los grupos de pines son congruentes con los primeros grupos diédricos y dicíclicos:

{\ displaystyle {\ begin {alineado} {\ mbox {Pin}} _ {+} (1) & \ cong \ mathrm {C} _ {2} \ times \ mathrm {C} _ {2} = {\ mbox {Dih}} _ {1} \\ {\ mbox {Pin}} _ {-} (1) & \ cong \ mathrm {C} _ {4} = {\ mbox {Dic}} _ {1}. \ final {alineado}}}

En 2 dimensiones, la distinción entre Pin ₊ y Pin _- refleja la distinción entre el grupo diedro de un 2 n -gon y el grupo dicíclico del grupo cíclico C _{2 n} .

En Pin ₊ , la preimagen del grupo diedro de un n -gon, considerado como un subgrupo Dih _n <O (2), es el grupo diedro de un 2 n -gon, Dih _{2 n} <Pin ₊ (2), mientras que en Pin _- , la preimagen del grupo diedro es el grupo dicíclico Dic _n <Pin _- (2).

El cuadrado conmutativo resultante de los subgrupos para Spin (2), Pin ₊ (2), SO (2), O (2) - es decir, C _{2 n} , Dih _{2 n} , C _n , Dih _n - también se obtiene utilizando la ortogonal proyectiva grupo (bajando de O por un cociente de 2 veces, en lugar de hacia arriba por una cubierta de 2 veces) en el cuadrado SO (2), O (2), PSO (2), PO (2), aunque en este caso también se realiza geométricamente, ya que "la proyectivización de un 2 n -gon en el círculo es un n -gon en la línea proyectiva".

En 3 dimensiones la situación es la siguiente. El álgebra de Clifford generada por 3 raíces cuadradas anticonmutación de +1 es el álgebra de matrices complejas 2 × 2, y Pin ₊ (3) es isomorfo a SO (3) × C ₄ . El álgebra de Clifford generada por 3 raíces cuadradas anticonmutación de -1 es el álgebra , y Pin _- (3) es isomorfo a SU (2) × C ₂ . Estos grupos no son isomorfos porque el centro de Pin ₊ (3) es C ₄ mientras que el centro de Pin _- (3) es C ₂ × C ₂ . ${\ Displaystyle \ mathbb {H} \ oplus \ mathbb {H}}$

Centrar

El centro de Pin (n, 0) = Pin ₊ es C ₂ cuando n es par, C ₂ × C ₂ cuando n = 1 mod 4 y C ₄ cuando n = 3 mod 4. El centro de Pin (0, n ) = Pin _- es C ₂ cuando n es par, C ₄ cuando n = 1 mod 4 y C ₂ × C ₂ cuando n = 3 mod 4. Para p , q ≠ 0 el centro de Pin (p, q) es una extensión de C ₂ × C ₂ o C ₄ por C ₂ .

Nombre

El nombre fue introducido en ( Atiyah, Bott & Shapiro 1964 , página 3, línea 17), donde dicen "Esta broma se debe a JP. Serre ". Es una formación posterior de Spin: "Pin es para O ( n ) como Spin es para SO ( n )", por lo tanto, al soltar la "S" de "Spin" se obtiene "Pin".

Notas

^ De hecho, son iguales como subconjuntos de GL ( V ), no solo isomorfos como grupos abstractos: un operador conserva una forma si y solo si conserva la forma negativa.
^ Se incluyen en diferentes álgebras, pero son iguales como subconjuntos de los espacios vectorialesy tienen la misma estructura de producto, por lo que se identifican naturalmente. ${\ Displaystyle \ mathrm {Cl} (n, 0) \ not \ cong \ mathrm {Cl} (0, n)}$ ${\ Displaystyle \ mathrm {Cl} (n, 0) = \ mathrm {Cl} (0, n) = \ Lambda ^ {*} \ mathbf {R} ^ {n}}$
^ A. Trautman (2001). "Cubiertas dobles de grupos pseudo-ortogonales". Análisis de Clifford y sus aplicaciones, serie científica de la OTAN . 25 : 377–388. doi : 10.1007 / 978-94-010-0862-4_32 . ISBN 978-0-7923-7045-1.

Referencias

Atiyah, MF ; Bott, R .; Shapiro, A. (1964), "Módulos de Clifford", Topología , 3, supl. 1: 3–38, doi : 10.1016 / 0040-9383 (64) 90003-5
M. Karoubi (1968). "Algèbres de Clifford et K-théorie" . Ana. Sci. CE. Norma. Sup . 1 (2): 161–270. doi : 10.24033 / asens.1163 .
Dabrowski, L. (1988), Acciones grupales sobre espinores , Bibliopolis, ISBN 88-7088-205-5
Carlip, S .; DeWitt-Morette, C. (1988), "Donde el signo de la métrica marca la diferencia", Phys. Rev. Lett. , 60 (16): 1599–1601, Bibcode : 1988PhRvL..60.1599C , doi : 10.1103 / physrevlett.60.1599 , PMID 10038088
Chamblin, A. (1994), "Sobre las obstrucciones a las estructuras de clavijas no Cliffordianas", Comm. Matemáticas. Phys. , 164 (1): 65–85, arXiv : gr-qc / 9509039 , Bibcode : 1994CMaPh.164 ... 65C , doi : 10.1007 / bf02108806 , S2CID 18305909
Lawson, H. Blaine; Michelsohn, Marie-Louise (1989). Gire la geometría . Prensa de la Universidad de Princeton . ISBN 978-0-691-08542-5.
Karoubi, Max (2008). K-Teoría . Saltador. págs. 212-214. ISBN 978-3-540-79889-7.

[1] De hecho, son iguales como subconjuntos de GL ( V ), no solo isomorfos como grupos abstractos: un operador conserva una forma si y solo si conserva la forma negativa.

[2] Se incluyen en diferentes álgebras, pero son iguales como subconjuntos de los espacios vectorialesy tienen la misma estructura de producto, por lo que se identifican naturalmente. ${\ Displaystyle \ mathrm {Cl} (n, 0) \ not \ cong \ mathrm {Cl} (0, n)}$ ${\ Displaystyle \ mathrm {Cl} (n, 0) = \ mathrm {Cl} (0, n) = \ Lambda ^ {*} \ mathbf {R} ^ {n}}$

[3] A. Trautman (2001). "Cubiertas dobles de grupos pseudo-ortogonales". Análisis de Clifford y sus aplicaciones, serie científica de la OTAN . 25 : 377–388. doi : 10.1007 / 978-94-010-0862-4_32 . ISBN 978-0-7923-7045-1.

[nota 1]