| Azulejos rombitrihexagonales | |
|---|---|
 | |
| Tipo | Azulejos semirregulares |
| Configuración de vértice | 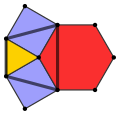 3.4.6.4 |
| Símbolo de Schläfli | rr {6,3} o |
| Símbolo de Wythoff | 3 | 6 2 |
| Diagrama de Coxeter |     |
| Simetría | p6m , [6,3], (* 632) |
| Simetría de rotación | p6 , [6,3] + , (632) |
| Acrónimo de Bowers | Rothat |
| Doble | Revestimiento deltoidal trihexagonal |
| Propiedades | Vértice-transitivo |
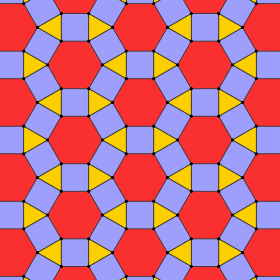
En geometría , el mosaico rombitrihexagonal es un mosaico semirregular del plano euclidiano . Hay un triángulo , dos cuadrados y un hexágono en cada vértice . Tiene el símbolo Schläfli de rr {3,6}.
John Conway lo llama rombihexadeltille . [1] Puede considerarse un cantelado por la terminología de Norman Johnson o un mosaico hexagonal expandido por el lenguaje operativo de Alicia Boole Stott .
Hay 3 mosaicos regulares y 8 semirregulares en el plano.
Colorantes uniformes [ editar ]
Solo hay una coloración uniforme en un mosaico rombitrihexagonal. (Nombrar los colores por índices alrededor de un vértice (3.4.6.4): 1232.)
Con los colores de borde hay una forma de semisimetría (3 * 3) o notación doble . Los hexágonos se pueden considerar como triángulos truncados, t {3} con dos tipos de aristas. Tiene diagrama de Coxeter 
, Símbolo de Schläfli s 2 {3,6}. El cuadrado bicolor se puede distorsionar en trapezoides isósceles . En el límite, donde los rectángulos degeneran en bordes, resulta un mosaico triangular , construido como un mosaico triangular chato,.
| Simetría | [6,3], (* 632) | [6,3 + ], (3 * 3) | ||
|---|---|---|---|---|
| Nombre | Rombitrihexagonal | Cantic chato triangular | Triangular chato | |
| Imagen | Coloración uniforme de la cara | Coloración uniforme de los bordes | Geometría no uniforme | Límite |
| Símbolo de Schläfli | rr {3,6} | s 2 {3,6} | s {3,6} | |
| Diagrama de Coxeter | | | | |
Ejemplos [ editar ]
De La gramática del ornamento (1856) | El juego Kensington | Suelo de baldosas, Museo Arqueológico de Sevilla , Sevilla, España | El templo de Diana en Nimes, Francia | Suelo de mosaico romano en Castel di Guido |
Azulejos relacionados [ editar ]
Hay un mosaico de 2 uniformes relacionado , que tiene hexágonos disecados en 6 triángulos. [3] [4]
3.4.6.4 | 3.3.4.3.4 y 3 6 |
El mosaico rombitrihexagonal se relaciona con el mosaico trihexagonal truncado reemplazando algunos de los hexágonos y cuadrados y triángulos circundantes con dodecágonos:
3.4.6.4 | 4.6.12 |
Embalaje circular [ editar ]
El mosaico rombitrihexagonal se puede utilizar como empaque circular , colocando círculos de igual diámetro en el centro de cada punto. Cada círculo está en contacto con otros 4 círculos en el embalaje ( número de besos ). [5] El dominio de la red traslacional (rombo rojo) contiene 6 círculos distintos.
Construcción de Wythoff [ editar ]
Hay ocho mosaicos uniformes que se pueden basar en el mosaico hexagonal regular (o el mosaico triangular dual ).
Al dibujar los mosaicos de color rojo en las caras originales, amarillo en los vértices originales y azul a lo largo de los bordes originales, hay 8 formas, 7 que son topológicamente distintas. (El mosaico triangular truncado es topológicamente idéntico al mosaico hexagonal).
| Azulejos uniformes hexagonales / triangulares | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetría : [6,3], (* 632) | [6,3] + (632) | [6,3 + ] (3 * 3) | |||||||||
| {6,3} | t {6,3} | r {6,3} | t {3,6} | {3,6} | rr {6,3} | tr {6,3} | sr {6,3} | s {3,6} | |||
| | | | | | | | | |||
| 6 3 | 3.12 2 | (3,6) 2 | 6.6.6 | 3 6 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 | 3.3.3.3.3.3 | |||
| Duales uniformes | |||||||||||
| V6 3 | V3.12 2 | V (3,6) 2 | V6 3 | V3 6 | V3.4.6.4 | V.4.6.12 | V3 4 .6 | V3 6 | |||
Mutaciones de simetría [ editar ]
Este mosaico está relacionado topológicamente como parte de una secuencia de poliedros cantelados con figura de vértice (3.4.n.4), y continúa como mosaicos del plano hiperbólico . Estas figuras transitivas de vértice tienen (* n32) simetría de reflexión .
| * n 32 mutación de simetría de teselaciones expandidas: 3.4. n. 4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simetría * n 32 [n, 3] | Esférico | Euclides. | Hyperb compacto. | Paracomp. | ||||
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3] ... | * ∞32 [∞, 3] | |
| Figura | ||||||||
| Config. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Revestimiento deltoidal trihexagonal [ editar ]
| Revestimiento deltoidal trihexagonal | |
|---|---|
| Tipo | Alicatado doble semirregular |
| Caras | cometa |
| Diagrama de Coxeter |  |
| Grupo de simetría | p6m, [6,3], (* 632) |
| Grupo de rotacion | p6, [6,3] + , (632) |
| Poliedro doble | Azulejos rombitrihexagonales |
| Configuración de la cara | V3.4.6.4 |
| Propiedades | cara transitiva |
El mosaico deltoidal trihexagonal es un doble del mosaico semirregular conocido como el mosaico rombitrihexagonal. Conway lo llama tetrille . [1] Los bordes de este mosaico se pueden formar mediante la superposición de intersección del mosaico triangular regular y un mosaico hexagonal . Cada cara de cometa de este mosaico tiene ángulos de 120 °, 90 °, 60 ° y 90 °. Es uno de los ocho mosaicos del plano en el que cada borde se encuentra en una línea de simetría del mosaico. [6]
El mosaico deltoidal trihexagonal es un mosaico dual del mosaico rombitrihexagonal de mosaico semirregular. [7] Sus caras son deltoides o cometas .
Poliedros y teselados relacionados [ editar ]
Es uno de los 7 mosaicos dobles uniformes en simetría hexagonal, incluidos los dobles regulares.
| Simetría : [6,3], (* 632) | [6,3] + , (632) | |||||
|---|---|---|---|---|---|---|
| V6 3 | V3.12 2 | V (3,6) 2 | V3 6 | V3.4.6.4 | V.4.6.12 | V3 4 .6 |
Este mosaico tiene variaciones transitivas de cara , que pueden distorsionar las cometas en trapezoides bilaterales o cuadriláteros más generales. Ignorando los colores de la cara a continuación, la simetría completa es p6m, y la simetría inferior es p31m con 3 espejos que se encuentran en un punto y 3 puntos de rotación. [8]
| Simetría | p6m, [6,3], (* 632) | p31m, [6,3 + ], (3 * 3) | |
|---|---|---|---|
| Formulario | |||
| Caras | cometa | Medio hexágono regular | Cuadriláteros |
Este mosaico está relacionado con el mosaico trihexagonal dividiendo los triángulos y hexágonos en triángulos centrales y fusionando los triángulos vecinos en cometas.
El mosaico deltoidal trihexagonal forma parte de un conjunto de mosaicos duales uniformes, correspondiente al dual del mosaico rombitrihexagonal.
Mutaciones de simetría [ editar ]
Este mosaico está relacionado topológicamente como parte de la secuencia de mosaicos con configuraciones de cara V3.4.n.4, y continúa como mosaicos del plano hiperbólico . Estas figuras transitivas de caras tienen (* n32) simetría de reflexión .
| Simetría * n 32 [n, 3] | Esférico | Euclides. | Hyperb compacto. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3] ... | * ∞32 [∞, 3] | |
| Figura Config. | V3.4.2.4 | V3.4.3.4 | V3.4.4.4 | V3.4.5.4 | V3.4.6.4 | V3.4.7.4 | V3.4.8.4 | V3.4.∞.4 |
Otro mosaico deltoidal (cometa) [ editar ]
Son posibles otras teselaciones deltoidales.
La simetría de puntos permite que el plano se llene con cometas en crecimiento, con la topología como un mosaico cuadrado , V4.4.4.4, y se puede crear cruzando la cuerda de un atrapasueños . A continuación se muestra un ejemplo con simetría hexagonal diedro.
Otro alicatado transitivo de cara con caras de cometa, también una variación topológica de un alicatado cuadrado y con configuración de cara V4.4.4.4. También es un vértice transitivo , con cada vértice que contiene todas las orientaciones de la cara de la cometa.
| Simetría | D 6 , [6], (* 66) | pmg, [∞, (2, ∞) + ], (22 *) | p6m, [6,3], (* 632) |
|---|---|---|---|
| Embaldosado | |||
| Configuración | V4.4.4.4 | V6.4.3.4 | |
Ver también [ editar ]
 | Wikimedia Commons tiene medios relacionados con el mosaico uniforme 3-4-6-4 (mosaico rombitrihexagonal) . |
- Mosaicos de polígonos regulares
- Lista de mosaicos uniformes
Notas [ editar ]
- ^ a b Tabla de Conway, 2008, p288
- ^ El anillo cicla una variación de la cadena de gatos
- ^ Chavey, D. (1989). "Mosaicos por polígonos regulares — II: un catálogo de mosaicos" . Computadoras y Matemáticas con Aplicaciones . 17 : 147-165. doi : 10.1016 / 0898-1221 (89) 90156-9 .
- ^ "Copia archivada" . Archivado desde el original el 9 de septiembre de 2006 . Consultado el 9 de septiembre de 2006 .Mantenimiento de CS1: copia archivada como título ( enlace )
- ↑ Order in Space: A design source book, Keith Critchlow, p.74-75, patrón B
- ^ Kirby, Matthew; Umble, Ronald (2011), "Teselaciones de bordes y rompecabezas plegables de sellos", Mathematics Magazine , 84 (4): 283–289, arXiv : 0908.3257 , doi : 10.4169 / math.mag.84.4.283 , MR 2843659 .
- ^ Weisstein, Eric W. "Doble teselación" . MathWorld . (Ver superposición comparativa de este mosaico y su doble)
- ^ Azulejos y patrones
Referencias [ editar ]
- Grünbaum, Branko ; Shephard, GC (1987). Azulejos y Patrones . Nueva York: WH Freeman. ISBN 0-7167-1193-1.(Capítulo 2.1: Azulejos regulares y uniformes , p. 58-65)
- Williams, Robert (1979). La base geométrica de la estructura natural: un libro fuente de diseño . Publicaciones de Dover, Inc. ISBN 0-486-23729-X. p40
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 [1] (Capítulo 21, Nombrar poliedros y teselaciones de Arquímedes y Cataluña.
- Weisstein, Eric W. "Teselado uniforme" . MathWorld .
- Weisstein, Eric W. "teselación semirregular" . MathWorld .
- Klitzing, Richard. "Azulejos euclidianos 2D x3o6x - rothat - O8" .
- Keith Critchlow, Order in Space: A design source book , 1970, pág. 69-61, Patrón N, Dual p. 77-76, patrón 2
- Dale Seymour y Jill Britton , Introducción a los teselados , 1989, ISBN 978-0866514613 , págs. 50–56, dual p. 116
