Cadena Steiner

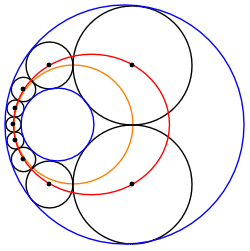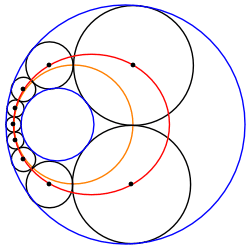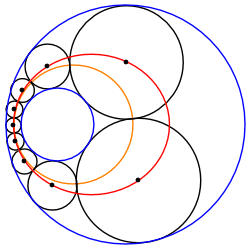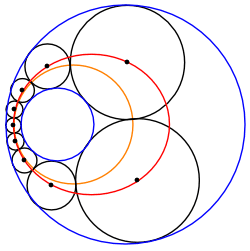
En geometría , una cadena de Steiner es un conjunto de n círculos, todos los cuales son tangentes a dos círculos dados que no se cruzan (azul y rojo en la Figura 1), donde n es finito y cada círculo de la cadena es tangente al anterior y siguientes círculos en la cadena. En las cadenas Steiner cerradas habituales , el primer y último ( n ^-ésimo ) círculo también son tangentes entre sí; por el contrario, en las cadenas Steiner abiertas , no es necesario que lo sean. Los círculos dados α y βno se cruzan, pero de lo contrario no están restringidos; el círculo más pequeño puede estar completamente dentro o fuera del círculo más grande. En estos casos, los centros de los círculos de cadena de Steiner se encuentran en una elipse o una hipérbola , respectivamente.

Las cadenas Steiner llevan el nombre de Jakob Steiner , quien las definió en el siglo XIX y descubrió muchas de sus propiedades. Un resultado fundamental es el porismo de Steiner , que afirma:

"Tangente de la misma manera" significa que el círculo arbitrario es interna o externamente tangente de la misma manera que un círculo de la cadena Steiner original. Un porísmo es un tipo de teorema que se relaciona con el número de soluciones y las condiciones de las mismas. Los porismos a menudo describen una figura geométrica que no puede existir a menos que se cumpla una condición, pero de lo contrario puede existir en un número infinito; otro ejemplo es el porismo de Poncelet .

El método de inversión de círculos es útil para tratar las cadenas de Steiner. Dado que conserva tangencias, ángulos y círculos, la inversión transforma una cadena de Steiner en otra del mismo número de círculos. Una elección particular de inversión transforma los círculos dados α y β en círculos concéntricos; en este caso, todos los círculos de la cadena Steiner tienen el mismo tamaño y pueden "rodar" en el espacio anular entre los círculos de forma similar a los rodamientos de bolas . Esta configuración estándar permite derivar varias propiedades de las cadenas de Steiner, por ejemplo, sus puntos de tangencia siempre se encuentran en un círculo. Existen varias generalizaciones de las cadenas de Steiner, más notablemente el hexlet de Soddy yCadenas de Pappus . ^[1]

Los 7 círculos de esta cadena Steiner (negro) son externamente tangentes al círculo interno dado (rojo) pero internamente tangentes al círculo externo dado (azul).

Los 7 círculos de esta cadena Steiner (negro) son externamente tangentes a ambos círculos dados (rojo y azul), que se encuentran fuera uno del otro.

Figura 1: Una cadena de Steiner de doce círculos negros ( n = 12) . Los círculos dados se muestran en azul y rojo, que son los círculos más externos e internos, respectivamente.

El radio de los círculos de Steiner es ρ mientras que los de los círculos internos y externos dados son r y R , respectivamente. La distancia desde el centro del círculo interior al centro de un círculo de Steiner es r + ρ (segmento de línea naranja).

Si incluso una cadena Steiner cerrada es posible para dos círculos dados (azul), entonces son posibles infinitas cadenas Steiner, todas relacionadas por rotación. Sus puntos de tangencia siempre caen en un círculo (naranja). Si los dos círculos dados están anidados, uno dentro del otro, los centros de los círculos de la cadena de Steiner (negro) caen en una elipse (rojo); de lo contrario, caen en una hipérbola .

El hexlet de Soddy es un análogo tridimensional de la cadena Steiner.