teorema del residuo
En el análisis complejo , el teorema del residuo , a veces llamado teorema del residuo de Cauchy , es una poderosa herramienta para evaluar integrales de línea de funciones analíticas sobre curvas cerradas; a menudo se puede usar para calcular integrales reales y también series infinitas . Generaliza el teorema integral de Cauchy y la fórmula integral de Cauchy . Desde una perspectiva geométrica, puede verse como un caso especial del teorema de Stokes generalizado .
Sea U un subconjunto abierto simplemente conexo del plano complejo que contiene una lista finita de puntos a 1 , ..., a n , U 0 = U \ { a 1 , …, a n } , y una función f definida y holomorfa en U 0 . Sea γ una curva cerrada rectificable en U 0 , y denotemos el número de vueltas de γ alrededor de unk poryo( γ , un k ). La integral de línea defalrededorγes igual a2 πi por la suma de losresiduosdefen los puntos, cada uno contado tantas veces comoγgira alrededor del punto:
Si γ es una curva cerrada simple orientada positivamente , I( γ , a k ) = 1 si a k está en el interior de γ , y 0 si no, por lo tanto
La relación del teorema del residuo con el teorema de Stokes viene dada por el teorema de la curva de Jordan . La curva plana general γ primero debe reducirse a un conjunto de curvas cerradas simples { γ i } cuyo total es equivalente a γ para propósitos de integración; esto reduce el problema a encontrar la integral de f dz a lo largo de una curva de Jordan γ i con interior V . El requisito de que f sea holomorfa en U 0 = U \ { a k } es equivalente al enunciado de quederivada exterior d ( f dz ) = 0 en U 0 . Así, si dos regiones planas V y W de U encierran el mismo subconjunto { a j } de { a k } , las regiones V \ W y W \ V se encuentran completamente en U 0 , y por lo tanto
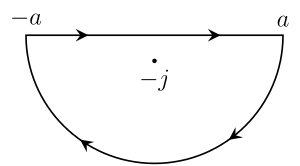
Para evaluar integrales reales se utiliza el teorema de los residuos de la siguiente manera: se extiende el integrando al plano complejo y se calculan sus residuos (que suele ser fácil), y se extiende una parte del eje real a una curva cerrada adjuntando un semicírculo en el semiplano superior o inferior, formando un semicírculo. La integral sobre esta curva se puede calcular usando el teorema del residuo. A menudo, la parte del semicírculo de la integral tenderá hacia cero a medida que crece el radio del semicírculo, dejando solo la parte del eje real de la integral, la que nos interesaba originalmente.
Surge en la teoría de probabilidades al calcular la función característica de la distribución de Cauchy . Resiste las técnicas del cálculo elemental pero puede evaluarse expresándolo como un límite de integrales de contorno .