centro homotetico

En geometría , un centro homotético (también llamado centro de similitud o centro de similitud ) es un punto desde el cual al menos dos figuras geométricamente similares pueden verse como una dilatación o contracción entre sí. Si el centro es exterior , las dos figuras son directamente semejantes entre sí; sus ángulos tienen el mismo sentido de rotación. Si el centro es interno , las dos figuras son imágenes especulares a escala una de la otra; sus ángulos tienen el sentido opuesto.

Si dos figuras geométricas poseen un centro homotético, son semejantes entre sí; en otras palabras, deben tener los mismos ángulos en los puntos correspondientes y diferir solo en su escala relativa. El centro homotético y las dos figuras no necesitan estar en el mismo plano; pueden estar relacionados por una proyección desde el centro homotético.

Los centros homotéticos pueden ser externos o internos. Si el centro es interno, las dos figuras geométricas son imágenes especulares a escala entre sí; en lenguaje técnico, tienen quiralidad opuesta . Un ángulo en el sentido de las agujas del reloj en una figura correspondería a un ángulo en el sentido contrario a las agujas del reloj en la otra. Por el contrario, si el centro es externo, las dos figuras son directamente similares entre sí; sus ángulos tienen el mismo sentido.

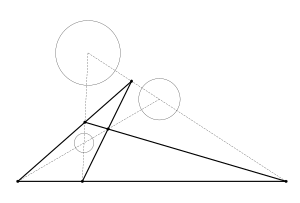
Los círculos son geométricamente similares entre sí y simétricos. Por lo tanto, un par de círculos tiene ambos tipos de centros homotéticos, internos y externos, a menos que los centros sean iguales o los radios sean iguales; estos casos excepcionales se tratan después de la posición general . Estos dos centros homotéticos se encuentran en la línea que une los centros de los dos círculos dados, que se llama línea de centros (Figura 3). También se pueden incluir círculos con radio cero (ver casos excepcionales), y también se puede utilizar radio negativo, alternando externo e interno.

Para un par dado de círculos, los centros homotéticos interno y externo se pueden encontrar de varias maneras. En geometría analítica , el centro homotético interno es el promedio ponderado de los centros de los círculos, ponderado por el radio del círculo opuesto: la distancia desde el centro del círculo hasta el centro interno es proporcional a ese radio, por lo que la ponderación es proporcional al radio opuesto . Denotando los centros de los círculos y por y y sus radios por y y denotando el centro por esto es:${\ estilo de visualización C_ {1}}$${\ estilo de visualización C_ {2}}$${\ estilo de visualización (x_ {1}, y_ {1})}$${\ estilo de visualización (x_ {2}, y_ {2})}$${\ estilo de visualización r_ {1}}$${\ estilo de visualización r_ {2}}$${\ estilo de visualización (x_ {0}, y_ {0}),}$

El centro externo se puede calcular por la misma ecuación, pero considerando uno de los radios como negativo; cualquiera de los dos produce la misma ecuación, que es:

Figura 1: El punto O es un centro homotético externo para los dos triángulos. El tamaño de cada figura es proporcional a su distancia del centro homotético.

Figura 2: Dos figuras geométricas relacionadas por un centro homotético externo S . Los ángulos en los puntos correspondientes son los mismos y tienen el mismo sentido; por ejemplo, los ángulos ABC y A'B'C' son ambos en sentido horario y de igual magnitud.

Los centros homotéticos externo (arriba) e interno (abajo) de los dos círculos (rojo) se muestran como puntos negros.

Figura 3: Dos círculos tienen ambos tipos de centros homotéticos, interno ( I ) y externo ( E ). Los radios de los círculos ( r ₁ y r ₂ ) son proporcionales a la distancia (d) de cada centro homotético. Los puntos A ₁ y A ₂ son homólogos, al igual que los puntos B ₁ y B ₂ .

Figura 4: Las líneas a través de los puntos antihomólogos correspondientes se cruzan en el eje radical de los dos círculos dados (verde y azul). Los puntos Q y P′ son antihomólogos, al igual que S y R′ . Estos cuatro puntos se encuentran en un círculo que corta a los dos círculos dados; las líneas que pasan por los puntos de intersección del nuevo círculo con los dos círculos dados deben cortarse en el centro radical G de los tres círculos, que se encuentra en el eje radical de los dos círculos dados.

Figura 5: Todo círculo que es tangente a dos círculos dados los toca en un par de puntos antihomólogos

Figura 6: Familia de círculos tangentes para el centro homotético externo

Figura 7: Familia de círculos tangentes para el centro homotético interno

Figura 8: El eje radical de círculos tangentes pasa por el centro radical

Figura 9: En una configuración de tres círculos, tres centros homotéticos (uno para cada par de círculos) se encuentran en una sola línea

Figura 10: Los seis centros homotéticos (puntos) de tres círculos se encuentran en cuatro líneas (líneas gruesas)

Figura 11: La línea azul es el eje radical de los dos círculos tangentes C ₁ y C ₂ (rosa). Cada par de círculos dados tiene un centro homotético que pertenece al eje radical de los dos círculos tangentes. Dado que el eje radical es una línea , esto significa que los tres centros homotéticos son colineales.