Complemento (teoría de conjuntos)

Establecer el concepto de teoría

... entonces el complemento de A es todo lo demás.

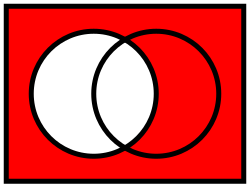
En la teoría de conjuntos , el complemento de un conjunto A , a menudo denota por A ^c (o A ' ), ^{[1] [2]} son los elementos que no están en A . ^[3]

Cuando se consideran todos los conjuntos bajo consideración para ser subconjuntos de un conjunto dado U , el complemento absoluto de A es el conjunto de elementos en U , pero no en A .

El complemento relativa de A con respecto a un conjunto B , también denominado el conjunto diferencia de B y A , escrito B \ A , es el conjunto de elementos de B pero no en una . ^[1]

Complemento absoluto

El complemento absoluto de A (de izquierda círculo) en U : .${\displaystyle A^{c}=U\setminus A}$

Definición

Si A es un conjunto, entonces el complemento absoluto de A (o simplemente el complemento de A ) es el conjunto de elementos que no están en A (dentro de un conjunto más grande que está implícitamente definido). En otras palabras, sea U un conjunto que contiene todos los elementos en estudio; si no es necesario mencionar U , ya sea porque se ha especificado previamente, o porque es obvio y único, entonces el complemento absoluto de A es el complemento relativo de A en U : ^[4]

${\displaystyle A^{c}=U-A}$.

O formalmente:

${\displaystyle A^{c}=\{x\in U\mid x\notin A\}.}$

El complemento absoluto de A generalmente se denota por A ^c . ^[1] Otras notaciones incluyen , , ^[3] , y . ^[5]${\displaystyle {\overline {A}}}$ ${\displaystyle A'}$ ${\displaystyle \complement _{U}A}$${\displaystyle \complement A}$

Ejemplos

• Suponga que el universo es el conjunto de números enteros . Si A es el conjunto de números impares, entonces el complemento de A es el conjunto de números pares. Si B es el conjunto de múltiplos de 3, entonces el complemento de B es el conjunto de números congruentes con 1 o 2 módulo 3 (o, en términos más simples, los enteros que no son múltiplos de 3).
• Suponga que el universo es la baraja estándar de 52 cartas . Si el conjunto A es el palo de espadas, entonces el complemento de A es la unión de los palos de tréboles, diamantes y corazones. Si el conjunto B es la unión de los palos de tréboles y diamantes, entonces el complemento de B es la unión de los palos de corazones y espadas.

Propiedades

Permiten una y B sean dos juegos en un universo U . Las siguientes identidades capturan propiedades importantes de complementos absolutos:

Leyes de De Morgan : ^[6]

• ${\displaystyle \left(A\cup B\right)^{c}=A^{c}\cap B^{c}.}$
• ${\displaystyle \left(A\cap B\right)^{c}=A^{c}\cup B^{c}.}$

Leyes de complemento: ^[6]

• ${\displaystyle A\cup A^{c}=U.}$
• ${\displaystyle A\cap A^{c}=\varnothing .}$
• ${\displaystyle \varnothing ^{c}=U.}$
• ${\displaystyle U^{c}=\varnothing .}$
• ${\displaystyle {\text{If }}A\subseteq B{\text{, then }}B^{c}\subseteq A^{c}.}$

  (esto se sigue de la equivalencia de un condicional con su contrapositivo ).

Ley de involución o doble complemento:

• ${\displaystyle \left(A^{c}\right)^{c}=A.}$

Relaciones entre complementos relativos y absolutos:

• ${\displaystyle A\setminus B=A\cap B^{c}.}$
• ${\displaystyle (A\setminus B)^{c}=A^{c}\cup B=A^{c}\cup (B\cap A).}$

Relación con diferencia de conjuntos:

• ${\displaystyle A^{c}\setminus B^{c}=B\setminus A.}$

Las dos primeras leyes del complemento anteriores muestran que si A es un no vacío, subconjunto propio de U , a continuación, { A , A ^c } es una partición de U .

Complemento relativo

Definición

Si A y B son conjuntos, entonces el complemento relativa de A en B , ^[6] también denominada la diferencia de conjuntos de B y A , ^[7] es el conjunto de elementos en B , pero no en A .

El complemento relativo de A (círculo izquierdo) en B (círculo derecho):${\displaystyle B\cap A^{c}=B\setminus A}$

El complemento relativo de A en B se denota B ∖ A según la norma ISO 31-11 . Se escribe a veces B - A , ^[1] pero esta notación es ambigua, ya que en algunos contextos se puede interpretar como el conjunto de todos los elementos de b - un , donde b se toma de B y una de A .

Formalmente:

${\displaystyle B\setminus A=\{x\in B\mid x\notin A\}.}$

Ejemplos

• ${\displaystyle \{1,2,3\}\setminus \{2,3,4\}=\{1\}}$.
• ${\displaystyle \{2,3,4\}\setminus \{1,2,3\}=\{4\}}$.
• Si es el conjunto de números reales y es el conjunto de números racionales , entonces es el conjunto de números irracionales .${\displaystyle \mathbb {R} }$${\displaystyle \mathbb {Q} }$${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$

Propiedades

Ver también: Lista de identidades y relaciones de conjuntos

Sean A , B y C tres conjuntos. Las siguientes identidades capturan propiedades notables de complementos relativos:

• ${\displaystyle C\setminus (A\cap B)=(C\setminus A)\cup (C\setminus B)}$.
• ${\displaystyle C\setminus (A\cup B)=(C\setminus A)\cap (C\setminus B)}$.
• ${\displaystyle C\setminus (B\setminus A)=(C\cap A)\cup (C\setminus B)}$,

  con el caso especial importante que demuestra que la intersección se puede expresar usando solo la operación de complemento relativo.${\displaystyle C\setminus (C\setminus A)=(C\cap A)}$

• ${\displaystyle (B\setminus A)\cap C=(B\cap C)\setminus A=B\cap (C\setminus A)}$.
• ${\displaystyle (B\setminus A)\cup C=(B\cup C)\setminus (A\setminus C)}$.
• ${\displaystyle A\setminus A=\emptyset }$.
• ${\displaystyle \emptyset \setminus A=\emptyset }$.
• ${\displaystyle A\setminus \emptyset =A}$.
• ${\displaystyle A\setminus U=\emptyset }$.

Relación complementaria

Una relación binaria R se define como un subconjunto de un producto de conjuntos de X × Y . La relación complementaria es el conjunto complemento de R en X × Y . El complemento de la relación R se puede escribir${\displaystyle {\bar {R}}}$

${\displaystyle {\bar {R}}\ =\ (X\times Y)\setminus R.}$

Aquí, R es a menudo visto como una matriz lógica con filas que representan los elementos de X , y elementos de columnas de Y . La verdad de aRb corresponde a 1 en la fila a , columna b . La producción de la relación complementaria a R corresponde a cambiar todos los 1 a 0 y los 0 a 1 para la matriz lógica del complemento.

Junto con la composición de relaciones y las relaciones recíprocas , las relaciones complementarias y el álgebra de conjuntos son las operaciones elementales del cálculo de relaciones .

Notación LaTeX

En el lenguaje de composición tipográfica LaTeX , el comando \setminus^[8] se usa generalmente para representar un símbolo de diferencia de conjunto, que es similar a un símbolo de barra invertida . Cuando se renderiza, el \setminuscomando se ve idéntico a \backslash, excepto que tiene un poco más de espacio delante y detrás de la barra, similar a la secuencia de LaTeX \mathbin{\backslash}. Hay una variante \smallsetminusdisponible en el paquete amssymb.

En lenguajes de programación

Algunos lenguajes de programación tienen conjuntos entre sus estructuras de datos incorporadas . Esta estructura de datos se comporta como un conjunto finito , es decir, consta de un número finito de datos que no están específicamente ordenados y, por tanto, pueden considerarse como elementos de un conjunto. En algunos casos, los elementos no son necesariamente distintos y la estructura de datos codifica conjuntos múltiples en lugar de conjuntos. Estos lenguajes de programación tienen operadores o funciones para calcular el complemento y el conjunto de diferencias.

Por lo general, estos operadores también se pueden aplicar a estructuras de datos que no son realmente conjuntos matemáticos, como listas ordenadas o matrices . De ello se deduce que algunos lenguajes de programación pueden tener una función llamada set_difference, incluso si no tienen ninguna estructura de datos para conjuntos.

Ver también

• Álgebra de conjuntos
• Intersección (teoría de conjuntos)
• Lista de identidades y relaciones establecidas
• Teoría de conjuntos ingenua
• Diferencia simétrica
• Unión (teoría de conjuntos)

Notas

1. "Compendio de símbolos matemáticos" . Bóveda de matemáticas . 2020-03-01 . Consultado el 4 de septiembre de 2020 .
2. "Complementar y establecer la diferencia" . web.mnstate.edu . Consultado el 4 de septiembre de 2020 .
3. "Definición de complemento (conjunto) (Diccionario ilustrado de matemáticas)" . www.mathsisfun.com . Consultado el 4 de septiembre de 2020 .
4. El conjunto en el que se considera el complemento se menciona así implícitamente en un complemento absoluto y explícitamente en un complemento relativo.
5. Bourbaki 1970 , p. E II.6.
6. Halmos , 1960 , p. 17.
7. Devlin 1979 , p. 6.
8. [1] La lista completa de símbolos LaTeX

Referencias

• Bourbaki, N. (1970). Théorie des ensembles (en francés). París: Hermann. ISBN 978-3-540-34034-8.
• Devlin, Keith J. (1979). Fundamentos de la teoría de conjuntos contemporánea . Universitext. Springer . ISBN 0-387-90441-7. Zbl  0407.04003 .
• Halmos, Paul R. (1960). Teoría de conjuntos ingenua . La Serie Universitaria en Matemáticas de Pregrado. van Nostrand Company. Zbl  0087.04403 .

Enlaces externos

• Weisstein, Eric W. "Complemento" . MathWorld .
• Weisstein, Eric W. "Complement Set" . MathWorld .