Álgebra exterior

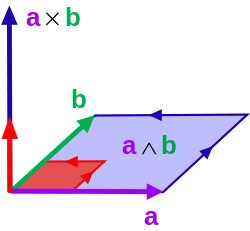
En matemáticas , el producto exterior o producto de cuña de los vectores es una construcción algebraica utilizada en geometría para estudiar áreas , volúmenes y sus análogos de dimensiones superiores. El producto exterior de dos vectores y  , denotado por , se llama bivector y vive en un espacio llamado cuadrado exterior , un espacio vectorial que es distinto del espacio original de vectores. La magnitud ^[3] de se puede interpretar como el área del paralelogramo con lados y ${\ Displaystyle u}$${\ Displaystyle v}$${\ Displaystyle u \ wedge v}$${\ Displaystyle u \ wedge v}$${\ Displaystyle u}$${\ Displaystyle v}$, que en tres dimensiones también se puede calcular utilizando el producto cruzado de los dos vectores. De manera más general, todas las superficies planas paralelas con la misma orientación y área tienen el mismo bivector como medida de su área orientada . Al igual que el producto cruzado, el producto exterior es anticomutativo , lo que significa que para todos los vectores y  , pero, a diferencia del producto cruzado, el producto exterior es asociativo .${\ Displaystyle u \ wedge v = - (v \ wedge u)}$${\ Displaystyle u}$${\ Displaystyle v}$

Cuando se considera de esta manera, el producto exterior de dos vectores se denomina 2 palas . De manera más general, el producto exterior de cualquier número k de vectores se puede definir y, a veces, se denomina k -cuchilla. Vive en un espacio conocido como el k- ésimo poder exterior. La magnitud de la k -cuchilla resultante es el hipervolumen orientado del paralelepípedo k -dimensional cuyas aristas son los vectores dados, así como la magnitud del producto triple escalar de vectores en tres dimensiones da el volumen del paralelepípedo generado por esos vectores.

El álgebra exterior , o álgebra de Grassmann después de Hermann Grassmann , ^[4] es el sistema algebraico cuyo producto es el producto exterior. El álgebra exterior proporciona un entorno algebraico en el que responder preguntas geométricas. Por ejemplo, las hojas tienen una interpretación geométrica concreta y los objetos del álgebra exterior se pueden manipular de acuerdo con un conjunto de reglas inequívocas. El álgebra exterior contiene objetos que no son sólo k- hojas, sino sumas de k- hojas; tal suma se llama k -vector . ^[5] La k-Las hojas, debido a que son productos simples de vectores, se denominan elementos simples del álgebra. El rango de cualquier k -vector se define como el número más pequeño de elementos simples de los que es una suma. El producto exterior se extiende al álgebra exterior completa, por lo que tiene sentido multiplicar dos elementos cualesquiera del álgebra. Equipado con este producto, el álgebra exterior es un álgebra asociativa , lo que significa que para cualquier elemento . Los k -vectores tienen grado k , lo que significa que son sumas de productos de k vectores. Cuando se multiplican elementos de diferentes grados, los grados se suman como una multiplicación de polinomios${\ Displaystyle \ alpha \ wedge (\ beta \ wedge \ gamma) = (\ alpha \ wedge \ beta) \ wedge \ gamma}$${\ Displaystyle \ alpha, \ beta, \ gamma}$. Esto significa que el álgebra exterior es un álgebra graduada .

La orientación invertida corresponde a negar el producto exterior.

Interpretación geométrica de elementos de grado n en un álgebra exterior real para n = 0 (punto con signo), 1 (segmento de línea dirigido o vector), 2 (elemento plano orientado), 3 (volumen orientado). El producto exterior de n vectores se puede visualizar como cualquier forma n- dimensional (p. Ej. N - paralelootopo , n - elipsoide ); con magnitud ( hipervolumen ) y orientación definida por la de su límite ( n - 1) dimensional y en qué lado está el interior. ^{[1] [2]}

El área de un paralelogramo en términos del determinante de la matriz de coordenadas de dos de sus vértices.

El producto cruzado ( vector azul ) en relación con el producto exterior ( paralelogramo azul claro ). La longitud del producto cruzado es la longitud del vector unitario paralelo ( rojo ) como el tamaño del producto exterior es el tamaño del paralelogramo de referencia ( rojo claro ).

Interpretación geométrica para el producto exterior de n 1-formas ( ε , η , ω ) para obtener una n- forma ("malla" de superficies coordinadas , aquí planos), ^[12] para n = 1, 2, 3 . Las "circulaciones" muestran orientación . ^{[13] [14]}