Cinco puntos determinan una cónica
En euclidiana y proyectiva geometría , al igual que dos (distintos) puntos determinan una línea (una curva plana grado-1), cinco puntos determinan una cónica (una curva plana grado-2). Hay sutilezas adicionales para las cónicas que no existen para las líneas y, por lo tanto, el enunciado y su prueba para las cónicas son más técnicas que para las líneas.
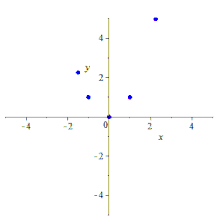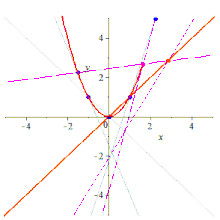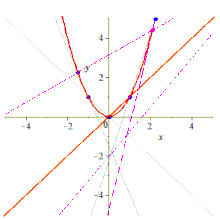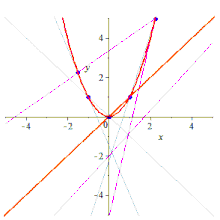
Formalmente, dados cualesquiera cinco puntos en el plano en posición lineal general , lo que significa que no hay tres colineales , hay una cónica única que pasa a través de ellos, que no será degenerada; esto es cierto tanto en el plano euclidiano como en cualquier plano proyectivo papiano . De hecho, dados cualesquiera cinco puntos hay una cónica que los atraviesa, pero si tres de los puntos son colineales, la cónica estará degenerada (reducible, porque contiene una línea) y puede que no sea única; ver discusión adicional .
Este resultado se puede probar de muchas formas diferentes; el argumento del recuento de dimensiones es el más directo y se generaliza en mayor grado, mientras que otras demostraciones son especiales para las cónicas.
Intuitivamente, pasar por cinco puntos en posición lineal general especifica cinco restricciones lineales independientes en el espacio lineal (proyectivo) de las cónicas y, por lo tanto, especifica una cónica única, aunque esta breve declaración ignora las sutilezas.
Las dos sutilezas del análisis anterior son que el punto resultante es una ecuación cuadrática (no una ecuación lineal) y que las restricciones son independientes. La primera es simple: si A , B y C desaparecen, entonces la ecuación define una línea, y 3 puntos cualesquiera en esta (de hecho, cualquier número de puntos) se encuentran en una línea; por lo tanto, la posición lineal general asegura una cónica. El segundo, que las restricciones son independientes, es significativamente más sutil: corresponde al hecho de que dados cinco puntos en posición lineal general en el plano, sus imágenes debajo del mapa de Veronese están en posición lineal general, lo cual es cierto porque el mapa de Veronese es birregular: es decir, si la imagen de cinco puntos satisface una relación, entonces la relación puede retirarse y los puntos originales también deben satisfacer una relación. El mapa de Veronese tiene coordenadas y el objetivo es dual al de las cónicas. El mapa de Veronese corresponde a la "evaluación de una cónica en un punto", y el enunciado sobre la independencia de las restricciones es exactamente un enunciado geométrico sobre este mapa.
![[x ^ {2}: xy: y ^ {2}: xz: yz: z ^ {2}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1902a3df10871523d42ac2a21cf4924de43786)
![[A B C D E F]](https://wikimedia.org/api/rest_v1/media/math/render/svg/58676be46552da77703fbfeb8fc14fda11841eb7)
Que cinco puntos determinan una cónica se puede probar mediante geometría sintética, es decir, en términos de líneas y puntos en el plano, además de la prueba analítica (algebraica) dada anteriormente. Tal demostración se puede dar usando un teorema de Jakob Steiner , [1] que establece:
