Teorema fundamental del cálculo
El teorema fundamental del cálculo es un teorema que vincula el concepto de diferenciar una función (calcular el gradiente) con el concepto de integrar una función (calcular el área bajo la curva). Las dos operaciones son inversas entre sí, aparte de un valor constante que depende de dónde se comienza a calcular el área.
La primera parte del teorema, a veces llamado el primer teorema fundamental del cálculo , establece que una de las antiderivadas (también conocida como integral indefinida ), digamos F , de alguna función f puede obtenerse como la integral de f con una variable cota de integración. Esto implica la existencia de antiderivadas para funciones continuas . [1]
A la inversa, la segunda parte del teorema, a veces llamado el segundo teorema fundamental del cálculo , establece que la integral de una función f en algún intervalo puede calcularse usando cualquiera, digamos F , de sus infinitas antiderivadas . Esta parte del teorema tiene aplicaciones prácticas clave, porque encontrar explícitamente la antiderivada de una función por integración simbólica evita la integración numérica para calcular integrales.
El teorema fundamental del cálculo relaciona diferenciación e integración, mostrando que estas dos operaciones son esencialmente inversas entre sí. Antes del descubrimiento de este teorema, no se reconocía que estas dos operaciones estuvieran relacionadas. Los matemáticos griegos antiguos sabían cómo calcular el área a través de infinitesimales , una operación que ahora llamaríamos integración. Los orígenes de la diferenciación también son anteriores al teorema fundamental del cálculo en cientos de años; Por ejemplo, en el siglo XIV las nociones de continuidad de funciones y movimiento fueron estudiadas por las Calculadoras de Oxford.y otros eruditos. La relevancia histórica del teorema fundamental del cálculo no es la capacidad de calcular estas operaciones, sino la comprensión de que las dos operaciones aparentemente distintas (cálculo de áreas geométricas y cálculo de gradientes) están en realidad estrechamente relacionadas.
La primera declaración publicada y prueba de una forma rudimentaria del teorema fundamental, de carácter fuertemente geométrico, [2] fue de James Gregory (1638-1675). [3] [4] Isaac Barrow (1630-1677) demostró una versión más generalizada del teorema, [5] mientras que su alumno Isaac Newton (1642-1727) completó el desarrollo de la teoría matemática circundante. Gottfried Leibniz (1646-1716) sistematizó el conocimiento en un cálculo para cantidades infinitesimales e introdujo la notación que se usa en la actualidad.
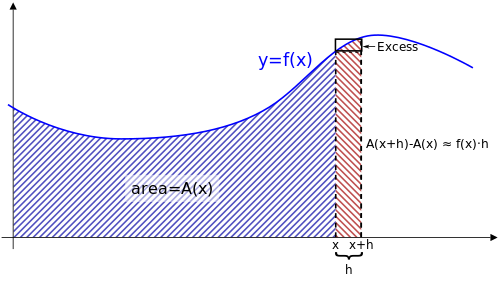
Para una función continua y = f ( x ) cuya gráfica se traza como una curva, cada valor de x tiene una función de área correspondiente A ( x ), que representa el área debajo de la curva entre 0 y x . Es posible que no se conozca la función A ( x ), pero se da por hecho que representa el área bajo la curva.