Conjunto parcialmente pedido

En matemáticas , especialmente en la teoría del orden , un conjunto parcialmente ordenado (también poset ) formaliza y generaliza el concepto intuitivo de una ordenación, secuencia o disposición de los elementos de un conjunto . Un poset consiste en un conjunto junto con una relación binaria que indica que, para ciertos pares de elementos del conjunto, uno de los elementos precede al otro en el orden. La relación en sí se llama un "orden parcial".

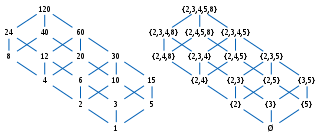
La palabra parcial en los nombres "orden parcial" y "conjunto parcialmente ordenado" se usa como una indicación de que no todos los pares de elementos deben ser comparables. Es decir, puede haber pares de elementos para los cuales ninguno de los elementos precede al otro en la poset. Los pedidos parciales generalizan así los pedidos totales , en los que cada par es comparable.

Un orden parcial define una noción de comparación . Dos elementos x e y pueden estar en cualquiera de las cuatro relaciones mutuamente excluyentes entre sí: x  <  y , o x  =  y , o x  >  y , o x e y son incomparables . ^{[1] [2]}

Un conjunto con un orden parcial se llama conjunto parcialmente ordenado (también llamado poset ). A veces también se usa el término conjunto ordenado , siempre que quede claro por el contexto que no se refiere a ningún otro tipo de orden. En particular, los conjuntos totalmente ordenados también pueden denominarse "conjuntos ordenados", especialmente en áreas donde estas estructuras son más comunes que los posets.

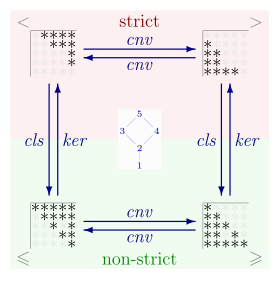
Una relación de orden parcial es una relación homogénea que es transitiva y antisimétrica . ^[4] Hay dos subdefiniciones comunes para una relación de orden parcial, para relaciones de orden parcial reflexivas e irreflexivas, también llamadas "no estrictas" y "estrictas" respectivamente. Las dos definiciones se pueden poner en una correspondencia uno a uno , por lo que para cada orden parcial estricto hay un único orden parcial no estricto correspondiente, y viceversa. El término orden parcial generalmente se refiere a una relación de orden parcial no estricta.

Un reflexivo , débil , ^[4] oel orden parcial no estricto ^[5] es unarelación homogénea≤ en unconjunto que esreflexivo,antisimétricoytransitivo. Es decir, por todolo que debe satisfacer:${\ estilo de visualización P}$${\ estilo de visualización a, b, c \ en P,}$

Fig.1 El diagrama de Hasse del conjunto de todos los subconjuntos de un conjunto de tres elementos ordenados por inclusión . Los conjuntos conectados por un camino ascendente, como y , son comparables, mientras que, por ejemplo, y no lo son.${\ estilo de visualización \ {x, y, z \},}$${\ estilo de visualización \ conjunto vacío}$${\ estilo de visualización \ {x, y \}}$${\ estilo de visualización \ {x \}}$${\ estilo de visualización \ {y \}}$

Fig.2 Diagrama conmutativo sobre las conexiones entre relaciones estrictas/no estrictas y sus duales, a través de las operaciones de cierre reflexivo ( cls ), kernel irreflexivo ( ker ) y relación inversa ( cnv ). Cada relación está representada por su matriz lógica para el poset cuyo diagrama de Hasse está representado en el centro. Por ejemplo , la fila 3, columna 4 de la matriz inferior izquierda está vacía.${\ estilo de visualización 3 \ no \ leq 4}$

Fig. 3 Gráfico de la divisibilidad de los números del 1 al 4. Este conjunto está parcialmente ordenado, pero no totalmente, porque existe una relación del 1 a cualquier otro número, pero no existe una relación del 2 al 3 o del 3 al 4.

Fig. 4b Pedido de productos en${\displaystyle \mathbb {N} \times \mathbb {N} }$

Fig. 4c Cierre reflexivo de orden directo estricto de productos en Los elementos cubiertos por (3, 3) y cubriendo (3, 3) se resaltan en verde y rojo, respectivamente.${\displaystyle \mathbb {N} \times \mathbb {N} .}$

Fig.5 La figura de arriba con los elementos mayores y menores eliminados. En esta pose reducida, la fila superior de elementos son todos elementos máximos , y la fila inferior son todos elementos mínimos , pero no hay elemento mayor ni menor .

Fig.6 Enteros no negativos, ordenados por divisibilidad

Fig.7a Mapa que preserva el orden, pero no refleja el orden (ya que f ( u ) ≼ f ( v ), pero no u v).${\ estilo de visualización \ leq}$

Fig.7b Isomorfismo de orden entre los divisores de 120 (parcialmente ordenados por divisibilidad) y los subconjuntos de divisores cerrados de {2, 3, 4, 5, 8 } (parcialmente ordenados por inclusión de conjuntos)