Punto isoperimétrico

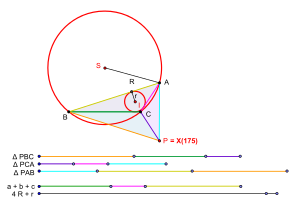
En geometría, el punto isoperimétrico es un punto especial asociado con un triángulo plano . El término fue introducido originalmente por GR Veldkamp en un artículo publicado en el American Mathematical Monthly en 1985 para denotar un punto P en el plano de un triángulo ABC que tiene la propiedad de que los triángulos PBC , PCA y PAB tienen isoperímetros, es decir, que tienen la propiedad que ^{[1] [2]}

PB + BC + CP = PC + CA + AP = PA + AB + BP .

Los puntos isoperimétricos en el sentido de Veldkamp existen solo para triángulos que satisfacen ciertas condiciones. El punto isoperimétrico del triángulo ABC en el sentido de Veldkamp, ​​si existe, tiene las siguientes coordenadas trilineales . ^[3]

(seg ( A / 2) cos ( B / 2) cos ( C / 2) - 1, seg ( B / 2) cos ( C / 2) cos ( A / 2) - 1, seg ( C / 2) cos ( A / 2) cos ( B / 2) - 1)

Dado cualquier triángulo ABC, se puede asociar con él un punto P que tenga coordenadas trilineales como se indica arriba. Este punto es un centro de triángulo y en la Enciclopedia de Centros de Triángulos (ETC) de Clark Kimberling se llama el punto isoperimétrico del triángulo ABC . Se designa como el centro del triángulo X (175). ^[4] El punto X (175) no necesita ser un punto isoperimétrico del triángulo ABC en el sentido de Veldkamp. Sin embargo, si existe el punto isoperimétrico del triángulo ABC en el sentido de Veldkamp, ​​entonces sería idéntico al punto X (175).

El punto P con la propiedad de que los triángulos PBC , PCA y PAB tienen perímetros iguales se ha estudiado ya en 1890 en un artículo de Emile Lemoine . ^{[4] [5]}

Existencia de un punto isoperimétrico en el sentido de Veldkamp

Un triángulo ABC en el que el centro del triángulo X (175) no es el punto isoperimétrico en el sentido de Veldkamp.

Sea ABC cualquier triángulo. Deje que los sidelengths de este triángulo sea una , b , y c . Sea su circunradio R y su radio interno r . La condición necesaria y suficiente para la existencia de un punto isoperimétrico en el sentido de Veldkamp se puede establecer como sigue. ^[1]

El triángulo ABC tiene un punto isoperimétrico en el sentido de Veldkamp si y solo si a + b + c > 4 R + r .

Para todos los triángulos de ángulos agudos ABC tenemos a + b + c > 4 R + r , por lo que todos los triángulos de ángulos agudos tienen puntos isoperimétricos en el sentido de Veldkamp.

Propiedades

Sea P el centro del triángulo X (175) del triángulo ABC . ^[4]

• P se encuentra en la línea que une el incentro y el punto de Gergonne del triángulo ABC .
• Si P es un punto isoperimétrico del triángulo ABC en el sentido de Veldkamp, ​​entonces los círculos de los triángulos PBC , PCA , PAB son por pares tangentes entre sí y P es su centro radical.
• Si P es un punto isoperimétrico del triángulo ABC en el sentido de Veldkamp, ​​entonces los perímetros de los triángulos PBC , PCA , PAB son iguales a 2 Δ / | (4 R + r - ( a + b + c )) | donde Δ es el área, R es el circunradio, r es el radio interno y a , b , c son las longitudes de los lados del triángulo ABC . ^[6]

Círculos de mierda

Círculos interiores y exteriores de Soddy en el caso de que el punto exterior de Soddy sea un punto isoperimétrico en el sentido de Veldkamp.

Círculos interiores y exteriores de Soddy en el caso de que el punto exterior de Soddy no sea un punto isoperimétrico en el sentido de Veldkamp.

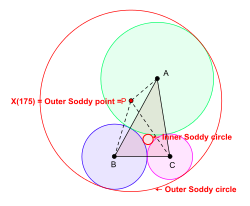
Dado un triángulo ABC, se pueden dibujar círculos en el plano del triángulo ABC con centros en A , B y C de manera que sean tangentes entre sí externamente. En general, se pueden dibujar dos nuevos círculos de modo que cada uno de ellos sea tangencial a los tres círculos con A , B , C como centros. (Uno de los círculos puede degenerar en una línea recta.) Estos círculos son los círculos Soddy del triángulo ABC . El círculo con el radio más pequeño es el círculo interior de Soddy y su centro se llama punto interior de Soddy o centro interior de Soddy.del triángulo ABC . El círculo con el radio más grande es el círculo Soddy exterior y su centro se llama el punto Soddy exterior o el centro Soddy exterior del triángulo ABC .^{[6] [7]}

El centro del triángulo X (175), el punto isoperimétrico en el sentido de Kimberling, es el punto Soddy exterior del triángulo ABC .

Referencias

1. G. R. Veldkamp (1985). "El punto isoperimétrico y el (los) punto (s) de igual desvío". Amer. Matemáticas. Mensual . 92 (8): 546–558. doi : 10.2307 / 2323159 . JSTOR  2323159 .
2. Hajja, Mowaffaq; Yff, Peter (2007). "El punto isoperimétrico y el (los) punto (s) de igual desvío en un triángulo". Revista de geometría . 87 (1–2): 76–82. doi : 10.1007 / s00022-007-1906-y . S2CID 122898960 . 
3. Kimberling, Clark. "Punto isoperimétrico e igual punto de desvío" . Consultado el 27 de mayo de 2012 .
4. Kimberling, Clark. "X (175) Punto isoperimétrico" . Archivado desde el original el 19 de abril de 2012 . Consultado el 27 de mayo de 2012 .
5. Se puede acceder al artículo de Emile Lemoine en Gallica. El artículo comienza en la página 111 y el punto se analiza en la página 126. Gallica
6. Nikolaos Dergiades (2007). "Los círculos Soddy" (PDF) . Foro Geometricorum . 7 : 191-197 . Consultado el 29 de mayo de 2012 .
7. "Círculos de mierda" . Consultado el 29 de mayo de 2012 .

enlaces externos

• Puntos de desvío isoperimétricos e iguales - ilustración interactiva en Geogebratube