Polinomio de Lagrange

En el análisis numérico , los polinomios de Lagrange se utilizan para la interpolación de polinomios . Para un conjunto dado de puntos sin dos valores iguales, el polinomio de Lagrange es el polinomio de menor grado que asume en cada valor el valor correspondiente .${\ Displaystyle (x_ {j}, y_ {j})}$${\ Displaystyle x_ {j}}$${\ Displaystyle x_ {j}}$${\ Displaystyle y_ {j}}$

Aunque lleva el nombre de Joseph-Louis Lagrange , quien lo publicó en 1795, el método fue descubierto por primera vez en 1779 por Edward Waring . ^[1] También es una consecuencia fácil de una fórmula publicada en 1783 por Leonhard Euler . ^[2]

Los usos de los polinomios de Lagrange incluyen el método Newton-Cotes de integración numérica y el esquema de intercambio secreto de Shamir en criptografía .

La interpolación de Lagrange es susceptible al fenómeno de gran oscilación de Runge. Como cambiar los puntos requiere recalcular todo el interpolante, a menudo es más fácil usar polinomios de Newton .${\ Displaystyle x_ {j}}$

donde no hay dos iguales, el polinomio de interpolación en la forma de Lagrange es una combinación lineal${\ Displaystyle x_ {j}}$

donde . Observe cómo, dada la suposición inicial de que no hay dos iguales, entonces (cuándo ) , por lo que esta expresión siempre está bien definida. La razón por la que los pares con no están permitidos es que no existiría ninguna función de interpolación ; una función solo puede obtener un valor para cada argumento . Por otro lado, si también , entonces esos dos puntos serían en realidad un solo punto.${\ Displaystyle 0 \ leq j \ leq k}$${\ Displaystyle x_ {j}}$${\ Displaystyle m \ neq j}$${\ Displaystyle x_ {j} -x_ {m} \ neq 0}$${\ Displaystyle x_ {i} = x_ {j}}$${\ Displaystyle y_ {i} \ neq y_ {j}}$${\ Displaystyle L}$${\ Displaystyle y_ {i} = L (x_ {i})}$${\ Displaystyle x_ {i}}$${\ Displaystyle y_ {i} = y_ {j}}$

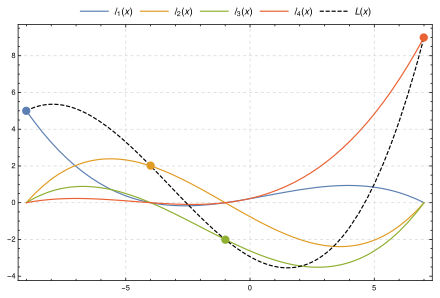
Esta imagen muestra, para cuatro puntos ( (−9, 5) , (−4, 2) , (−1, −2) , (7, 9) ), el polinomio de interpolación (cúbico) L ( x ) (discontinuo, negro), que es la suma de los polinomios base escalados y ₀ ℓ ₀ ( x ) , y ₁ ℓ ₁ ( x ) , y ₂ ℓ ₂ ( x ) y y ₃ ℓ ₃ ( x ). El polinomio de interpolación pasa por los cuatro puntos de control, y cada polinomio base escalado pasa por su respectivo punto de control y es 0 donde x corresponde a los otros tres puntos de control.

Aquí trazamos las funciones de base de Lagrange de primer, segundo y tercer orden en un dominio de dos unidades. Se utilizan combinaciones lineales de funciones de base de Lagrange para construir polinomios de interpolación de Lagrange. Las funciones de base de Lagrange se utilizan comúnmente en el análisis de elementos finitos como bases para las funciones de forma de los elementos. Además, es común utilizar un dominio de dos unidades como espacio natural para la definición del elemento finito.

Ejemplo de divergencia de interpolación para un conjunto de polinomios de Lagrange.