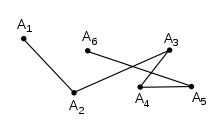
En geometría , una cadena poligonal es una serie conectada de segmentos de línea . Más formalmente, una cadena poligonal P es una curva especificada por una secuencia de puntos llamados vértices . La curva en sí consiste en los segmentos de línea que conectan los vértices consecutivos.
Nombre [ editar ]
Una cadena poligonal también puede denominarse curva poligonal , [1] trayectoria poligonal , [2] polilínea , [3] curva lineal por partes , [3] línea discontinua [4] o, en los sistemas de información geográfica , cadena lineal o anillo lineal . [5]
Variaciones [ editar ]
Una cadena poligonal simple es aquella en la que solo los segmentos consecutivos (o el primero y el último) se cruzan y solo en sus extremos.
Una cadena poligonal cerrada es aquella en la que el primer vértice coincide con el último o, alternativamente, el primero y el último vértices también están conectados por un segmento de línea. [6] Una cadena poligonal cerrada simple en el plano es el límite de un polígono simple . A menudo, el término " polígono " se usa con el significado de "cadena poligonal cerrada", pero en algunos casos es importante hacer una distinción entre un área poligonal y una cadena poligonal.
Una cadena poligonal se llama monótona , si hay una línea recta L tal que cada línea perpendicular a L interseca la cadena como máximo una vez. Cada cadena poligonal monótona no trivial está abierta. En comparación, un polígono monótono es un polígono (una cadena cerrada) que se puede dividir en exactamente dos cadenas monótonas. [7] Las gráficas de funciones lineales por partes forman cadenas monótonas con respecto a una línea horizontal.
Propiedades [ editar ]
Cada conjunto de al menos puntos contiene una trayectoria poligonal de al menos aristas en las que todas las pendientes tienen el mismo signo. Este es un corolario del teorema de Erdős-Szekeres .
Aplicaciones [ editar ]
Las cadenas poligonales se pueden utilizar a menudo para aproximar curvas más complejas. En este contexto, el algoritmo Ramer-Douglas-Peucker se puede utilizar para encontrar una cadena poligonal con pocos segmentos que sirva como una aproximación precisa. [8] [9]
En el dibujo de gráficos , las cadenas poligonales se utilizan a menudo para representar los bordes de los gráficos, en estilos de dibujo en los que dibujar los bordes como segmentos de línea recta causaría cruces, colisiones borde-vértice u otras características no deseadas. En este contexto, a menudo se desea dibujar bordes con el menor número posible de segmentos y curvas, para reducir el desorden visual en el dibujo; el problema de minimizar el número de dobleces se denomina minimización de dobleces . [10]
Las cadenas poligonales también son un tipo de datos fundamental en geometría computacional . Por ejemplo, un algoritmo de ubicación de puntos de Lee y Preparata opera descomponiendo subdivisiones planas arbitrarias en una secuencia ordenada de cadenas monótonas, en las que un problema de consulta de ubicación de puntos puede resolverse mediante una búsqueda binaria ; este método se perfeccionó posteriormente para proporcionar límites de tiempo óptimos para el problema de ubicación de puntos. [11]
Con el sistema de información geográfica , las cadenas de líneas pueden representar cualquier geometría lineal y pueden describirse utilizando el conocido marcado de texto como LineString o MultiLineString . [5] Los anillos lineales (o LinearRing ) son cadenas poligonales cerradas y simples que se utilizan para construir geometrías poligonales.
Ver también [ editar ]
- Cadena (topología algebraica) , una combinación formal de simples que en el caso unidimensional incluye cadenas poligonales
- Curva compuesta de Bézier , una generalización que reemplaza cada línea recta de una cadena poligonal por una curva suave.
- Distancia de enlace , la cantidad de segmentos de la cadena más corta que une dos puntos dentro de un polígono
- Regresión por partes
- Path (teoría de grafos) , un concepto análogo en grafos abstractos
- Terreno poliédrico , una generalización 3D de una cadena poligonal monótona
- Número de palo , un nudo invariante basado en representar un nudo como una cadena poligonal cerrada
- Traverse , aplicación en topografía
Referencias [ editar ]
- ^ Gomes, Jonas; Velho, Luiz; Costa Sousa, Mario (2012), Computer Graphics: Theory and Practice , CRC Press, p. 186, ISBN 9781568815800.
- ^ Cheney, Ward (2001), Análisis de matemáticas aplicadas , Textos de posgrado en matemáticas, 208 , Springer, p. 13, ISBN 9780387952796.
- ↑ a b Boissonnat, Jean-Daniel; Teillaud, Monique (2006), Geometría computacional efectiva para curvas y superficies , Springer, p. 34, ISBN 9783540332596.
- ^ Muggeo, Vito MR (mayo de 2008), "segmentado: un paquete R para adaptarse a modelos de regresión con relaciones de línea discontinua" (PDF) , R News , 8 (1): 20-25
- ^ a b Open Geospatial Consortium ( 28 de mayo de 2011 ), Herring, John R. (ed.), Estándar de implementación de OpenGIS® para información geográfica - Acceso a funciones simples - Parte 1: Arquitectura común , 1.2.1, Open Geospatial Consortium , consultado el 15 de enero de 2016
- ^ Mehlhorn, Kurt ; Näher, Stefan (1999), LEDA: A Platform for Combinatorial and Geometric Computing , Cambridge University Press, pág. 758, ISBN 9780521563291.
- ^ O'Rourke, Joseph (1998), Geometría computacional en C , Cambridge Tracts in Theoretical Computer Science, Cambridge University Press, p. 45, ISBN 9780521649766.
- ^ Ramer, Urs (1972), "Un procedimiento iterativo para la aproximación poligonal de curvas planas", Procesamiento de imágenes y gráficos por computadora , 1 (3): 244-256, doi : 10.1016 / S0146-664X (72) 80017-0.
- ^ Douglas, David; Peucker, Thomas (1973), "Algoritmos para la reducción del número de puntos necesarios para representar una línea digitalizada o su caricatura", The Canadian Cartographer , 10 (2): 112-122, doi : 10.3138 / FM57-6770-U75U -7727.
- ^ Tamassia, Roberto (1987), "Al incrustar un gráfico en la cuadrícula con el número mínimo de curvas", SIAM Journal on Computing , 16 (3): 421–444, doi : 10.1137 / 0216030.
- ^ Edelsbrunner, Herbert ; Guibas, Leonidas J .; Stolfi, Jorge (1986), "Ubicación óptima del punto en una subdivisión monótona", SIAM Journal on Computing , 15 (2): 317–340, doi : 10.1137 / 0215023.