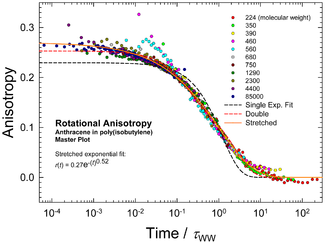
Función exponencial estirada
se obtiene insertando una ley de potencia fraccionaria en la función exponencial . En la mayoría de las aplicaciones, solo tiene sentido para los argumentos t entre 0 y + ∞. Con β = 1, se recupera la función exponencial habitual. Con un exponente de estiramiento β entre 0 y 1, la gráfica de log f versus t se estira característicamente , de ahí el nombre de la función. La función exponencial comprimida (con β > 1) tiene menos importancia práctica, con la notable excepción de β = 2, que da la distribución normal .
En matemáticas, la exponencial estirada también se conoce como distribución complementaria acumulativa de Weibull . La exponencial estirada es también la función característica , básicamente la transformada de Fourier , de la distribución alfa estable simétrica de Lévy .
En física, la función exponencial estirada se usa a menudo como una descripción fenomenológica de la relajación en sistemas desordenados. Fue introducido por primera vez por Rudolf Kohlrausch en 1854 para describir la descarga de un condensador; [1] por lo que también se conoce como función de Kohlrausch . En 1970, G. Williams y DC Watts utilizaron la transformada de Fourier de la exponencial estirada para describir los espectros dieléctricos de los polímeros; [2] en este contexto, la exponencial estirada o su transformada de Fourier también se denominan función Kohlrausch-Williams-Watts (KWW) .
En aplicaciones fenomenológicas, a menudo no está claro si la función exponencial estirada debe usarse para describir la función de distribución diferencial o integral, o ninguna de las dos. En cada caso, se obtiene la misma desintegración asintótica, pero un prefactor de ley de potencia diferente, lo que hace que los ajustes sean más ambiguos que para las exponenciales simples. En unos pocos casos, [3] [4] [5] [6] se puede demostrar que la desintegración asintótica es una exponencial estirada, pero el prefactor suele ser una potencia no relacionada.
Siguiendo la interpretación física habitual, interpretamos el argumento de la función t como tiempo, y f β ( t ) es la distribución diferencial. Por tanto, el área bajo la curva se puede interpretar como un tiempo medio de relajación . Uno encuentra
En física, se han hecho intentos para explicar el comportamiento exponencial extendido como una superposición lineal de desintegraciones exponenciales simples. Esto requiere una distribución no trivial de los tiempos de relajación, ρ (u) , que está implícitamente definida por