Método de Euler semi-implícito

En matemáticas, el método de Euler semi-implícita , también llamado simpléctico Euler , Euler semi-explícita , Euler-Cromer , y Newton-Stormer-Verlet (NSV) , es una modificación del método de Euler para resolver ecuaciones de Hamilton , un sistema de ordinario ecuaciones diferenciales que surge en la mecánica clásica . Es un integrador simpléctico y, por lo tanto, produce mejores resultados que el método de Euler estándar.

Configuración

El método de Euler semi-implícito se puede aplicar a un par de ecuaciones diferenciales de la forma

${\displaystyle {dx \over dt}=f(t,v)}$^{[ cita requerida ]}

${\displaystyle {dv \over dt}=g(t,x),}$

donde f y g son funciones dadas. Aquí, x y v pueden ser escalares o vectores. Las ecuaciones de movimiento en la mecánica hamiltoniana toman esta forma si el hamiltoniano es de la forma

${\displaystyle H=T(t,v)+V(t,x).\,}$

Las ecuaciones diferenciales deben resolverse con la condición inicial

${\displaystyle x(t_{0})=x_{0},\qquad v(t_{0})=v_{0}.}$

El método

El método de Euler semi-implícito produce una solución discreta aproximada iterando

${\displaystyle {\begin{aligned}v_{n+1}&=v_{n}+g(t_{n},x_{n})\,\Delta t\\[0.3em]x_{n+1}&=x_{n}+f(t_{n},v_{n+1})\,\Delta t\end{aligned}}}$

donde Δ t es el paso de tiempo y t _n = t ₀ + n Δ t es el tiempo después de n pasos.

La diferencia con el método de Euler estándar es que el método de Euler semi-implícito usa v _{n +1} en la ecuación para x _{n +1} , mientras que el método de Euler usa v _n .

La aplicación del método con el paso tiempo negativo para el cálculo de desde y reordenando lleva a la segunda variante del método de Euler semi-implícito${\displaystyle (x_{n},v_{n})}$${\displaystyle (x_{n+1},v_{n+1})}$

${\displaystyle {\begin{aligned}x_{n+1}&=x_{n}+f(t_{n},v_{n})\,\Delta t\\[0.3em]v_{n+1}&=v_{n}+g(t_{n},x_{n+1})\,\Delta t\end{aligned}}}$

que tiene propiedades similares.

El Euler semi-implícito es un integrador de primer orden , al igual que el método de Euler estándar. Esto significa que comete un error global del orden de Δt. Sin embargo, el método de Euler semi-implícito es un integrador simpléctico , a diferencia del método estándar. Como consecuencia, el método de Euler semi-implícito casi conserva la energía (cuando el hamiltoniano es independiente del tiempo). A menudo, la energía aumenta de manera constante cuando se aplica el método estándar de Euler, lo que lo hace mucho menos preciso.

Alternar entre las dos variantes del método de Euler semi-implícito conduce en una simplificación a la integración Störmer- Verlet y en una simplificación ligeramente diferente a la integración de salto , aumentando tanto el orden del error como el orden de conservación de la energía. ^[1]

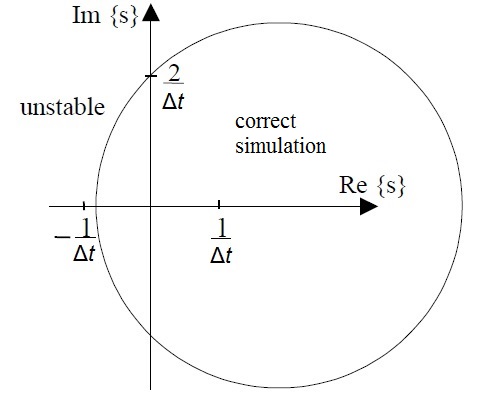
La región de estabilidad del método semi-implícito fue presentada por Niiranen ^[2] aunque el Euler semi-implícito fue llamado erróneamente Euler simétrico en su artículo. El método semi-implícito modela el sistema simulado correctamente si las raíces complejas de la ecuación característica están dentro del círculo que se muestra a continuación. Para las raíces reales, la región de estabilidad se extiende fuera del círculo para el cual el criterio es${\displaystyle s>-2/\Delta t}$

Como puede verse, el método semi-implícito puede simular correctamente tanto sistemas estables que tienen sus raíces en el semiplano izquierdo como sistemas inestables que tienen sus raíces en el semiplano derecho. Esta es una clara ventaja sobre Euler hacia adelante (estándar) y Euler hacia atrás. Adelante Euler tiende a tener menos amortiguamiento que el sistema real cuando las partes reales negativas de las raíces se acercan al eje imaginario y hacia atrás Euler puede mostrar que el sistema es estable incluso cuando las raíces están en el semiplano derecho.

Ejemplo

El movimiento de un resorte que satisface la ley de Hooke viene dado por

${\displaystyle {\begin{aligned}{\frac {dx}{dt}}&=v(t)\\[0.2em]{\frac {dv}{dt}}&=-{\frac {k}{m}}\,x=-\omega ^{2}\,x.\end{aligned}}}$

El Euler semi-implícito para esta ecuación es

${\displaystyle {\begin{aligned}v_{n+1}&=v_{n}-\omega ^{2}\,x_{n}\,\Delta t\\[0.2em]x_{n+1}&=x_{n}+v_{n+1}\,\Delta t.\end{aligned}}}$

Sustituyendo en la segunda ecuación con la expresión dada por la primera ecuación, la iteración se puede expresar en la siguiente forma matricial${\displaystyle v_{n+1}}$

${\displaystyle {\begin{bmatrix}x_{n+1}\\v_{n+1}\end{bmatrix}}={\begin{bmatrix}1-\omega ^{2}\Delta t^{2}&\Delta t\\-\omega ^{2}\Delta t&1\end{bmatrix}}{\begin{bmatrix}x_{n}\\v_{n}\end{bmatrix}},}$

y dado que el determinante de la matriz es 1, la transformación conserva el área.

La iteración conserva la energía modificada funcional exactamente, lo que lleva a órbitas periódicas estables (para un tamaño de paso suficientemente pequeño) que se desvían de las órbitas exactas. La frecuencia circular exacta aumenta en la aproximación numérica en un factor de .${\displaystyle E_{h}(x,v)={\tfrac {1}{2}}\left(v^{2}+\omega ^{2}\,x^{2}-\omega ^{2}\Delta t\,vx\right)}$${\displaystyle O(\Delta t)}$${\displaystyle \omega }$${\displaystyle 1+{\tfrac {1}{24}}\omega ^{2}\Delta t^{2}+O(\Delta t^{4})}$

Referencias

1. Hairer, Ernst; Lubich, Christian; Wanner, Gerhard (2003). "Integración numérica geométrica ilustrada por el método Störmer / Verlet". Acta Numerica . 12 : 399–450. CiteSeerX  10.1.1.7.7106 . doi : 10.1017 / S0962492902000144 .
2. Niiranen, Jouko: algoritmo de Euler simétrico rápido y preciso para simulaciones electromecánicas Proceedings of the Electrimacs'99, 14-16 de septiembre de 1999 Lisboa, Portugal, vol. 1, páginas 71 - 78.

• Giordano, Nicholas J .; Hisao Nakanishi (julio de 2005). Física Computacional (2ª ed.). Benjamin Cummings. ISBN 0-13-146990-8.
• MacDonald, James. "El método Euler-Cromer" . Universidad de Delaware . Consultado el 11 de abril de 2013 .
• Vesely, Franz J. (2001). Física Computacional: Introducción (2ª ed.). Saltador. págs.  117 . ISBN 978-0-306-46631-1.