Funciones elípticas de Jacobi

En matemáticas , las funciones elípticas de Jacobi son un conjunto de funciones elípticas básicas . Se encuentran en la descripción del movimiento de un péndulo (ver también péndulo (matemáticas) ), así como en el diseño de filtros elípticos electrónicos . Mientras que las funciones trigonométricas se definen con referencia a un círculo, las funciones elípticas de Jacobi son una generalización que se refieren a otras secciones cónicas , la elipse en particular. La relación con las funciones trigonométricas está contenida en la notación, por ejemplo, mediante la notación coincidente para${\ estilo de visualización \ nombre del operador {sn}}$${\ estilo de visualización \ pecado}$. Las funciones elípticas de Jacobi se utilizan con más frecuencia en problemas prácticos que las funciones elípticas de Weierstrass, ya que no requieren nociones de análisis complejo para ser definidas y/o comprendidas. Fueron introducidos por Carl Gustav Jakob Jacobi  ( 1829 ). Carl Friedrich Gauss ya había estudiado las funciones elípticas especiales de Jacobi en 1797, en particular las funciones elípticas de la lemniscata , ^[1] pero su trabajo se publicó mucho más tarde.

Hay doce funciones elípticas de Jacobi denotadas por , donde y son cualquiera de las letras , , y . (Las funciones de la forma se establecen trivialmente en la unidad para completar la notación). es el argumento y es el parámetro, los cuales pueden ser complejos.${\displaystyle \operatorname {pq} (u,m)}$${\displaystyle \mathrm {p} }$${\displaystyle \mathrm {q} }$${\displaystyle \mathrm {c} }$${\displaystyle \mathrm {s} }$${\displaystyle \mathrm {n} }$${\displaystyle \mathrm {d} }$${\displaystyle \operatorname {pp} (u,m)}$${\displaystyle u}$${\displaystyle m}$

El rectángulo fundamental en el plano complejo de ${\displaystyle u}$

Función elíptica de Jacobi ${\displaystyle \operatorname {cn} }$

Función elíptica de Jacobi ${\displaystyle \operatorname {dn} }$

Función elíptica de Jacobi ${\displaystyle \operatorname {sc} }$

Gráficos de cuatro funciones elípticas de Jacobi en el plano complejo de , que ilustran su comportamiento periódico doble. Imágenes generadas usando una versión del método de coloreado de dominios . ^[3] Todos tienen valores de igual a .${\displaystyle u}$${\displaystyle k={\sqrt {m}}}$${\displaystyle 0.8}$

Modelo de amplitud (medida a lo largo del eje vertical) en función de las variables independientes u y k

Gráfico de la elipse de Jacobi ( x ² + y ² /b ² =1, b real) y las doce funciones elípticas de Jacobi pq(u,m) para valores particulares de ángulo φ y parámetro b . La curva continua es la elipse, con m =1-1/b ² y u = F(φ,m) donde F(.,.) es la integral elíptica de primera clase (con parámetro ). La curva punteada es el círculo unitario. Las líneas tangentes del círculo y la elipse en x=cd que cruzan el eje x en dc se muestran en gris claro.${\displaystyle m=k^{2}}$

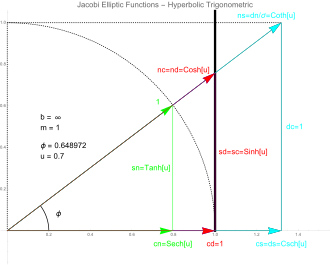
Gráfico de la curva de Jacobi degenerada ( x ²  +  y ² / b ²  = 1, b  = ∞) y las doce funciones elípticas de Jacobi pq( u ,1) para un valor particular del ángulo  φ . La curva sólida es la elipse degenerada ( x ²  = 1) con m  = 1 y u  =  F ( φ ,1) donde F (·,\middot') es la integral elíptica de primera especie. La curva punteada es el círculo unitario. Como estas son las funciones de Jacobi para m = 0 (funciones trigonométricas circulares) pero con argumentos imaginarios, corresponden a las seis funciones trigonométricas hiperbólicas.

Gráfico de la hipérbola de Jacobi ( x ²  +  y ² / b ²  = 1, b imaginaria) y las doce funciones elípticas de Jacobi pq( u , m ) para valores particulares del ángulo φ y el parámetro b . La curva sólida es la hipérbola, con m  = 1 − 1/ b ² y u  =  F ( φ , m ) donde F (·,·) es la integral elíptica de primera especie. La curva punteada es el círculo unitario. Para el triángulo ds-dc, σ = sen( φ )cos( φ ).

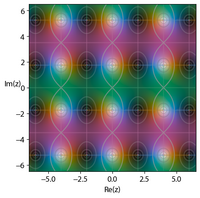
Gráficas de la fase para las doce funciones elípticas de Jacobi pq(u,m) como un argumento complejo de función u, con polos y ceros indicados. Las gráficas son sobre un ciclo completo en las direcciones real e imaginaria con la parte coloreada que indica la fase de acuerdo con la rueda de color en la parte inferior derecha (que reemplaza la función dd trivial). Las regiones con una amplitud inferior a 1/3 se colorean de negro, lo que indica aproximadamente la ubicación de un cero, mientras que las regiones con una amplitud superior a 3 se colorean de blanco, lo que indica aproximadamente la posición de un polo. Todas las parcelas usan m  = 2/3 con K  =  K ( m ), K ′ =  K (1 −  m ), K(·) siendo la integral elíptica completa de primera especie. Las flechas en los polos apuntan en la dirección de la fase cero. Las flechas derecha e izquierda implican residuos reales positivos y negativos respectivamente. Las flechas hacia arriba y hacia abajo implican residuos imaginarios positivos y negativos, respectivamente.