Teorema de Poncelet-Steiner
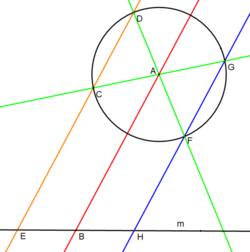
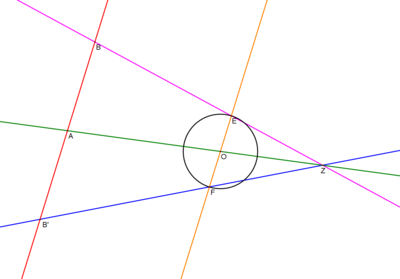
En la rama de las matemáticas conocida como geometría euclidiana , el teorema de Poncelet-Steiner es uno de varios resultados relacionados con las construcciones de compás y regla con restricciones adicionales impuestas. Este resultado establece que cualquier cosa que se pueda construir con regla y compás juntos se puede construir solo con regla, siempre que se den un solo círculo y su centro . Este teorema está relacionado con la equivalencia de la brújula oxidada .
Aunque una brújula puede facilitar significativamente las construcciones, se da a entender que no hay un propósito funcional de la brújula una vez que se ha dibujado el primer círculo. Todas las construcciones siguen siendo posibles, aunque se entiende naturalmente que los círculos y sus arcos no pueden dibujarse sin el compás. Esto significa solo que la brújula puede usarse con fines estéticos , más que con fines de construcción. Todos los puntos que definen de manera única una construcción, que se pueden determinar con el uso de la brújula, son igualmente determinables sin ella.
Las construcciones realizadas de acuerdo con este teorema, que se basan únicamente en el uso de una herramienta de regla sin la ayuda de un compás, se conocen como construcciones de Steiner . Las construcciones de Steiner pueden involucrar cualquier número de círculos, incluso ninguno, ya dibujado en el plano, con o sin sus centros.
En el siglo X, el matemático persa Abu al-Wafa' Buzjani (940-998) consideró construcciones geométricas usando una regla y un compás con una abertura fija, el llamado compás oxidado . Las construcciones de este tipo parecían tener algún significado práctico, ya que fueron utilizadas por los artistas Leonardo da Vinci y Albrecht Dürer en Europa a fines del siglo XV. Un nuevo punto de vista se desarrolló a mediados del siglo XVI cuando el tamaño de la abertura se consideró fijo pero arbitrario y la cuestión de cuántas construcciones de Euclides se podían obtener era primordial. [1]
El matemático renacentista Lodovico Ferrari , alumno de Gerolamo Cardano en un "desafío matemático" contra Niccolò Fontana Tartaglia pudo demostrar que "todo Euclides" (es decir, las construcciones con regla y compás en los primeros seis libros de los Elementos de Euclides ) podría ser logrado con una regla y un compás oxidado. En diez años, Cardano, Tartaglia y el estudiante de Tartaglia, Benedetti, obtuvieron conjuntos adicionales de soluciones. Durante el siglo siguiente, estas soluciones fueron generalmente olvidadas hasta que, en 1673, Georg Mohr publicó (de forma anónima y en holandés) Euclidis Curiosique contiene sus propias soluciones. Mohr solo había oído hablar de la existencia de los resultados anteriores y esto lo llevó a trabajar en el problema. [2]
Demostrar que "todo Euclides" se puede realizar con regla y compás oxidado no es lo mismo que demostrar que todas las construcciones con regla y compás se pueden realizar con regla y solo un compás oxidado. Tal prueba requeriría la formalización de lo que podría construir una regla y un compás. Este trabajo preliminar fue proporcionado por Jean Victor Poncelet en 1822, motivado por el trabajo de Mohr sobre el teorema de Mohr-Mascheroni . También conjeturó y sugirió una posible prueba de que una regla y un compás oxidado serían equivalentes a una regla y un compás, y además, el compás oxidado solo necesita usarse una vez. El resultado de que una regla y un solo círculo con centro dado es equivalente a una regla y un compás fue demostrado porJakob Steiner en 1833. [3] [1]