Número de enlace
En matemáticas , el número de enlace es un invariante numérico que describe el enlace de dos curvas cerradas en un espacio tridimensional . Intuitivamente, el número de enlace representa el número de veces que cada curva se enrolla alrededor de la otra. El número de enlace es siempre un número entero , pero puede ser positivo o negativo según la orientación de las dos curvas. (Esto no es cierto para las curvas en la mayoría de las variedades tridimensionales, donde los números de enlace también pueden ser fracciones o simplemente no existir).
El número de enlace fue introducido por Gauss en forma de integral de enlace . Es un importante objeto de estudio en teoría de nudos , topología algebraica y geometría diferencial , y tiene numerosas aplicaciones en matemáticas y ciencias , incluida la mecánica cuántica , el electromagnetismo y el estudio del superenrollamiento del ADN .
Dos curvas cerradas cualesquiera en el espacio, si se permite que pasen a través de sí mismas pero no entre sí, se pueden mover exactamente a una de las siguientes posiciones estándar. Esto determina el número de enlace:
Cada curva puede pasar a través de sí misma durante este movimiento, pero las dos curvas deben permanecer separadas en todo momento. Esto se formaliza como homotopía regular , que además requiere que cada curva sea una inmersión , no cualquier mapa. Sin embargo, esta condición agregada no cambia la definición de número de enlace (no importa si se requiere que las curvas sean siempre inmersiones o no), que es un ejemplo de un principio h (principio de homotopía), lo que significa que la geometría se reduce a la topología.
Este hecho (que el número de enlace es el único invariante) se prueba más fácilmente colocando un círculo en la posición estándar y luego mostrando que el número de enlace es el único invariante del otro círculo. En detalle:
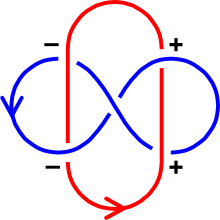
Existe un algoritmo para calcular el número de enlace de dos curvas a partir de un diagrama de enlace . Etiqueta cada cruce como positivo o negativo , de acuerdo con la siguiente regla: [1]