Navegación de círculo máximo
La navegación ortodrómica o ortodrómica (relacionada con el rumbo ortodrómico ; del griego ορθóς , ángulo recto, y δρóμος , camino) es la práctica de navegar un buque (un barco o un avión ) a lo largo de un gran círculo . Tales rutas producen la distancia más corta entre dos puntos del globo. [1]
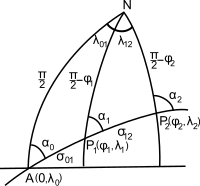
La trayectoria del gran círculo se puede encontrar usando trigonometría esférica ; esta es la versión esférica del problema geodésico inverso . Si un navegante comienza en P 1 = (φ 1 ,λ 1 ) y planea recorrer el gran círculo hasta un punto en el punto P 2 = (φ 2 ,λ 2 ) (ver Fig. 1, φ es la latitud, positiva hacia el norte , y λ es la longitud, positiva hacia el este), los cursos inicial y final α 1 y α 2 están dados por fórmulas para resolver un triángulo esférico
donde λ 12 = λ 2 − λ 1 [nota 1] y los cuadrantes de α 1 ,α 2 están determinados por los signos del numerador y el denominador en las fórmulas tangentes (p. ej., usando la función atan2 ). El ángulo central entre los dos puntos, σ 12 , viene dado por
(El numerador de esta fórmula contiene las cantidades que se usaron para determinar tanα 1 ). La distancia a lo largo del gran círculo será entonces s 12 = R σ 12 , donde R es el radio supuesto de la tierra y σ 12 se expresa en radianes . Utilizando el radio terrestre medio , R = R 1 ≈ 6371 km (3959 mi) produce resultados para la distancia s 12 que están dentro del 1% de la longitud geodésica para el elipsoide WGS84 ; consulte Geodésicas en un elipsoide para obtener más detalles.
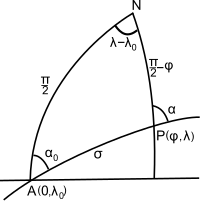
Para encontrar los puntos de paso , es decir, las posiciones de los puntos seleccionados en el gran círculo entre P 1 y P 2 , primero extrapolamos el gran círculo a su nodo A , el punto en el que el gran círculo cruza el ecuador en el norte. dirección: sea la longitud de este punto λ 0 — ver Fig. 1. El acimut en este punto, α 0 , está dado por
Sean las distancias angulares a lo largo del gran círculo de A a P 1 y P 2 σ 01 y σ 02 respectivamente. Entonces usando las reglas de Napier tenemos