Partición (teoría de números)

Descomposición de un número entero como suma de números enteros positivos

Diagramas jóvenes asociados a las particiones de los enteros positivos del 1 al 8. Están dispuestos de modo que las imágenes bajo la reflexión sobre la diagonal principal del cuadrado sean particiones conjugadas.

Particiones de n con mayor sumando k

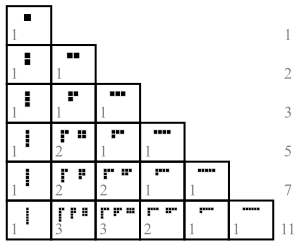
En teoría de números y combinatoria , una partición de un entero positivo n , también llamada partición de entero , es una forma de escribir n como una suma de enteros positivos. Dos sumas que difieren solo en el orden de sus sumandos se consideran la misma partición. (Si el orden importa, la suma se convierte en una composición ). Por ejemplo, 4 se puede dividir de cinco formas distintas:

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

La composición dependiente del orden 1 + 3 es la misma partición que 3 + 1, mientras que las dos composiciones distintas 1 + 2 + 1 y 1 + 1 + 2 representan la misma partición 2 + 1 + 1.

Un sumando en una partición también se llama parte . El número de particiones de n viene dado por la función de partición p ( n ). Entonces p (4) = 5. La notación λ ⊢ n significa que λ es una partición de n .

Las particiones se pueden visualizar gráficamente con diagramas de Young o diagramas de Ferrers . Ocurren en varias ramas de las matemáticas y la física , incluido el estudio de polinomios simétricos y del grupo simétrico y en la teoría de la representación de grupos en general.

Ejemplos

Las siete particiones de 5 son:

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

En algunas fuentes, las particiones se tratan como una secuencia de sumandos, más que como una expresión con signos más. Por ejemplo, la partición 2 + 2 + 1 podría escribirse como la tupla (2, 2, 1) o en la forma aún más compacta (2 ² , 1) donde el superíndice indica el número de repeticiones de un término.

Representaciones de particiones

Hay dos métodos de diagramación comunes para representar particiones: como diagramas de Ferrers, que llevan el nombre de Norman Macleod Ferrers , y como diagramas de Young, que llevan el nombre del matemático británico Alfred Young . Ambos tienen varias convenciones posibles; aquí, usamos notación en inglés , con diagramas alineados en la esquina superior izquierda.

Diagrama de Ferrers

La partición 6 + 4 + 3 + 1 del número positivo 14 se puede representar mediante el siguiente diagrama:

Los 14 círculos están alineados en 4 filas, cada una del tamaño de una parte de la partición. Los diagramas para las 5 particiones del número 4 se enumeran a continuación:

4	=	3 + 1	=	2 + 2	=	2 + 1 + 1	=	1 + 1 + 1 + 1

Diagrama joven

Una representación visual alternativa de una partición entera es su diagrama de Young (a menudo también llamado diagrama de Ferrers). En lugar de representar una partición con puntos, como en el diagrama de Ferrers, el diagrama de Young usa cuadros o cuadrados. Por tanto, el diagrama de Young para la partición 5 + 4 + 1 es

mientras que el diagrama de Ferrers para la misma partición es

Si bien esta variación aparentemente trivial no parece digna de mención aparte, los diagramas de Young resultan ser extremadamente útiles en el estudio de las funciones simétricas y la teoría de la representación de grupos : llenar las casillas de los diagramas de Young con números (oa veces objetos más complicados) que obedecen a varios reglas conduce a una familia de objetos llamados cuadros de Young , y estos cuadros tienen un significado combinatorio y teórico de la representación. ^[1] Como un tipo de forma hecha por cuadrados adyacentes unidos entre sí, los diagramas de Young son un tipo especial de poliomino . ^[2]

Función de partición

Usando el método de Euler para encontrar p (40): una regla con signos más y menos (caja gris) se desliza hacia abajo, los términos relevantes se suman o se restan. Las posiciones de los signos vienen dadas por diferencias de números naturales (azules) e impares (naranjas) alternados. En el archivo SVG, coloque el cursor sobre la imagen para mover la regla.

La función de partición ${\displaystyle p(n)}$representa el número de posibles particiones de un entero no negativo${\displaystyle n}$. Por ejemplo,${\displaystyle p(4)=5}$ porque el entero ${\displaystyle 4}$ tiene las cinco particiones ${\displaystyle 1+1+1+1}$, ${\displaystyle 1+1+2}$, ${\displaystyle 1+3}$, ${\displaystyle 2+2}$, y ${\displaystyle 4}$. Los valores de esta función para${\displaystyle n=0,1,2,\dots }$ son:

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ... (secuencia A000041 en la OEIS ).

La función generadora de ${\displaystyle p}$ es

${\displaystyle \sum _{n=0}^{\infty }p(n)q^{n}=\prod _{j=1}^{\infty }\sum _{i=0}^{\infty }q^{ji}=\prod _{j=1}^{\infty }(1-q^{j})^{-1}.}$

No se conoce ninguna expresión de forma cerrada para la función de partición, pero tiene expansiones asintóticas que la aproximan con precisión y relaciones de recurrencia mediante las cuales se puede calcular con exactitud. Crece como una función exponencial de la raíz cuadrada de su argumento. ^[3] El inverso multiplicativo de su función generadora es la función de Euler ; según el teorema del número pentagonal de Euler, esta función es una suma alterna de las potencias del número pentagonal de su argumento.

${\displaystyle p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+\cdots }$

Srinivasa Ramanujan descubrió por primera vez que la función de partición tiene patrones no triviales en aritmética modular , ahora conocidos como congruencias de Ramanujan . Por ejemplo, siempre que la representación decimal de${\displaystyle n}$ termina en el dígito 4 o 9, el número de particiones de ${\displaystyle n}$será divisible por 5. ^[4]

Particiones restringidas

Tanto en la combinatoria como en la teoría de números, a menudo se estudian familias de particiones sujetas a diversas restricciones. ^[5] Esta sección analiza algunas de esas restricciones.

Particiones conjugadas y auto-conjugadas

Si volteamos el diagrama de la partición 6 + 4 + 3 + 1 a lo largo de su diagonal principal, obtenemos otra partición de 14:

	↔
6 + 4 + 3 + 1	=	4 + 3 + 3 + 2 + 1 + 1

Al convertir las filas en columnas, obtenemos la partición 4 + 3 + 3 + 2 + 1 + 1 del número 14. Se dice que estas particiones están conjugadas entre sí. ^[6] En el caso del número 4, las particiones 4 y 1 + 1 + 1 + 1 son pares conjugados, y las particiones 3 + 1 y 2 + 1 + 1 están conjugadas entre sí. De particular interés es la partición 2 + 2, que tiene a sí misma como conjugada. Se dice que tal partición es autoconjugada . ^[7]

Reclamación : El número de particiones autoconjugadas es el mismo que el número de particiones con distintas partes impares.

Prueba (esquema) : La observación crucial es que cada parte impar se puede " doblar " en el medio para formar un diagrama autoconjugado:

↔

Entonces se puede obtener una biyección entre el conjunto de particiones con distintas partes impares y el conjunto de particiones autoconjugadas, como se ilustra en el siguiente ejemplo:

	↔
9 + 7 + 3	=	5 + 5 + 4 + 3 + 2
Dist. impar		auto-conjugado

Partes impares y partes distintas

Entre las 22 particiones del número 8, hay 6 que contienen solo partes impares :

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Alternativamente, podríamos contar particiones en las que ningún número aparece más de una vez. Tal partición se llama partición con partes distintas . Si contamos las particiones de 8 con partes distintas, también obtenemos 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

Esta es una propiedad general. Para cada número positivo, el número de particiones con partes impares es igual al número de particiones con partes distintas, denotado por q ( n ). ^{[8] [9]} Este resultado fue probado por Leonhard Euler en 1748 ^[10] y más tarde se generalizó como teorema de Glaisher .

Para cada tipo de partición restringida hay una función correspondiente para el número de particiones que satisfacen la restricción dada. Un ejemplo importante es q ( n ). Los primeros valores de q ( n ) son (comenzando con q (0) = 1):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (secuencia A000009 en la OEIS ).

La función generadora de q ( n ) (particiones en partes distintas) viene dada por ^[11]

${\displaystyle \sum _{n=0}^{\infty }q(n)x^{n}=\prod _{k=1}^{\infty }(1+x^{k})=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}.}$

El teorema del número pentagonal da una recurrencia para q : ^[12]

q ( k ) = una _k + q ( k - 1) + q ( k - 2) - q ( k - 5) - q ( k - 7) + q ( k - 12) + q ( k - 15) - q ( k - 22) - ...

donde a _k es (−1) ^m si k = 3 m ² - m para algún entero my es 0 en caso contrario.

Tamaño de pieza restringido o número de piezas

Al tomar conjugados, el número p _k ( n ) de particiones de n en exactamente k partes es igual al número de particiones de n en las que la parte más grande tiene un tamaño k . La función p _k ( n ) satisface la recurrencia

p _k ( norte ) = p _k ( norte - k ) + p _{k −1} ( n - 1)

con valores iniciales p ₀ (0) = 1 y p _k ( n ) = 0 si n ≤ 0 o k ≤ 0 y n y k no son ambos cero. ^[13]

Se recupera la función p ( n ) por

${\displaystyle p(n)=\sum _{k=0}^{n}p_{k}(n).}$

Una posible función generadora para tales particiones, tomando k fijo yn variable, es

${\displaystyle \sum _{n\geq 0}p_{k}(n)x^{n}=x^{k}\cdot \prod _{i=1}^{k}{\frac {1}{1-x^{i}}}.}$

De manera más general, si T es un conjunto de enteros positivos, entonces el número de particiones de n , todas cuyas partes pertenecen a T , tiene una función generadora

${\displaystyle \prod _{t\in T}(1-x^{t})^{-1}.}$

Esto se puede usar para resolver problemas de cambio (donde el conjunto T especifica las monedas disponibles). Como dos casos particulares, uno tiene que el número de particiones de n en el que todas las partes son 1 o 2 (o, de manera equivalente, el número de particiones de n en 1 o 2 partes) es

${\displaystyle \left\lfloor {\frac {n}{2}}+1\right\rfloor ,}$

y el número de particiones de n en el que todas las partes son 1, 2 o 3 (o, de manera equivalente, el número de particiones de n en tres partes como máximo) es el número entero más cercano a ( n + 3) ² / 12. ^{[14 ]}

Asintótica

La tasa de crecimiento asintótica para p ( n ) está dada por

${\displaystyle \log p(n)\sim C{\sqrt {n}}{\text{ as }}n\rightarrow \infty }$

donde ${\displaystyle C=\pi {\sqrt {\frac {2}{3}}}.}$. ^[15] La fórmula asintótica más precisa

${\displaystyle p(n)\sim {\frac {1}{4n{\sqrt {3}}}}\exp \left({\pi {\sqrt {\frac {2n}{3}}}}\right)}$ como ${\displaystyle n\rightarrow \infty }$

fue obtenido por primera vez por GH Hardy y Ramanujan en 1918 e independientemente por JV Uspensky en 1920. Una expansión asintótica completa fue dada en 1937 por Hans Rademacher .

Si A es un conjunto de números naturales, dejamos que p _A ( n ) denota el número de particiones de n en elementos de A . Si A posee una densidad natural positiva α entonces

${\displaystyle \log p_{A}(n)\sim C{\sqrt {\alpha n}}}$

ya la inversa, si esta propiedad asintótica se cumple para p _A ( n ), entonces A tiene una densidad natural α. ^[16] Este resultado fue declarado, con un bosquejo de la prueba, por Erdős en 1942. ^{[17] [18]}

Si A es un conjunto finito, este análisis no se aplica (la densidad de un conjunto finito es cero). Si A tiene k elementos cuyo máximo común divisor es 1, entonces ^[19]

${\displaystyle p_{A}(n)=\left(\prod _{a\in A}a^{-1}\right)\cdot {\frac {n^{k-1}}{(k-1)!}}+O(n^{k-2}).}$

Particiones en un rectángulo y coeficientes binomiales gaussianos

También se puede limitar simultáneamente el número y el tamaño de las piezas. Let p ( N , M ; n ) denotan el número de particiones de n con al mayoría de M partes, cada una de tamaño como máximo N . De manera equivalente, estas son las particiones cuyo diagrama de Young encaja dentro de un rectángulo M × N. Existe una relación de recurrencia

${\displaystyle p(N,M;n)=p(N,M-1;n)+p(N-1,M;n-M)}$

obtenido al observar que ${\displaystyle p(N,M;n)-p(N,M-1;n)}$cuenta las particiones de n en exactamente M partes de tamaño como máximo N , y al restar 1 de cada parte de dicha partición se obtiene una partición de n - M en como máximo M partes. ^[20]

El coeficiente binomial gaussiano se define como:

${\displaystyle {k+\ell \choose \ell }_{q}={k+\ell \choose k}_{q}={\frac {\prod _{j=1}^{k+\ell }(1-q^{j})}{\prod _{j=1}^{k}(1-q^{j})\prod _{j=1}^{\ell }(1-q^{j})}}.}$

El coeficiente binomial de Gauss está relacionado con la función generadora de p ( N , M ; n ) por la igualdad

${\displaystyle \sum _{n=0}^{MN}p(N,M;n)q^{n}={M+N \choose M}_{q}.}$

Rango y cuadrado de Durfee

El rango de una partición es el número más grande k tal que la partición contiene al menos k partes de tamaño al menos k . Por ejemplo, la partición 4 + 3 + 3 + 2 + 1 + 1 tiene rango 3 porque contiene 3 partes que son ≥ 3, pero no contiene 4 partes que son ≥ 4. En el diagrama de Ferrers o diagrama de Young de una partición de rango r , el cuadrado r × r de las entradas en la parte superior izquierda se conoce como el cuadrado de Durfee :

El cuadrado de Durfee tiene aplicaciones dentro de la combinatoria en las pruebas de varias identidades de partición. ^[21] También tiene cierta importancia práctica en la forma del índice h .

Una estadística diferente también se denomina a veces rango de una partición (o rango de Dyson), es decir, la diferencia${\displaystyle \lambda _{k}-k}$para una partición de k piezas con la mayor parte${\displaystyle \lambda _{k}}$. Esta estadística (que no está relacionada con la descrita anteriormente) aparece en el estudio de las congruencias de Ramanujan .

Celosía de Young

Existe un orden parcial natural en las particiones dado por la inclusión de diagramas de Young. Este conjunto parcialmente ordenado se conoce como celosía de Young . La celosía se definió originalmente en el contexto de la teoría de la representación , donde se utiliza para describir las representaciones irreductibles de grupos simétricos S _n para todo n , junto con sus propiedades de ramificación, en la característica cero. También ha recibido un estudio significativo por sus propiedades puramente combinatorias; en particular, es el ejemplo motivador de un poset diferencial .

Ver también

• Rango de una partición , una noción diferente de rango
• Manivela de una partición
• Orden de dominación
• Factorización
• Factorización de enteros
• Partición de un conjunto
• Estrellas y barras (combinatoria)
• Partición de plano
• Número educado , definido por particiones en enteros consecutivos
• Partición multiplicativa
• Doce veces
• Fórmula de muestreo de Ewens
• La fórmula de Faà di Bruno
• Multipartición
• Identidades de Newton
• Función de piezas más pequeñas
• Una partición de Goldbach es la partición de un número par en números primos (ver la conjetura de Goldbach )
• Función de partición de Kostant

Notas

1. Andrews 1976 , p. 199.
2. Josuat-Vergès, Matthieu (2010), "Bijections entre rellenos que evitan patrones de diagramas de Young", Journal of Combinatorial Theory , Serie A, 117 (8): 1218-1230, arXiv : 0801.4928 , doi : 10.1016 / j.jcta .2010.03.006 , MR  2.677.686 , S2CID  15392503.
3. Andrews 1976 , p. 69.
4. Hardy y Wright 2008 , p. 380.
5. Aliso, Henry L. (1969). "Partición de identidades - desde Euler hasta el presente" . American Mathematical Monthly . 76 (7): 733–746. doi : 10.2307 / 2317861 . JSTOR 2317861 . 
6. Hardy y Wright 2008 , p. 362.
7. Hardy y Wright 2008 , p. 368.
8. Hardy y Wright 2008 , p. 365.
9. notación sigue a Abramowitz y Stegun 1964 , p. 825
10. Andrews, George E. (1971). Teoría de números . Filadelfia: WB Saunders Company. págs. 149–50.
11. Abramowitz y Stegun , 1964 , p. 825, 24,2,2 eq. Yo (b)
12. Abramowitz y Stegun , 1964 , p. 826, 24.2.2 eq. II (A)
13. Richard Stanley, Combinatoria enumerativa , volumen 1, segunda edición. Cambridge University Press, 2012. Capítulo 1, sección 1.7.
14. Hardy, GH (1920). Algunos problemas famosos de la teoría de los números . Prensa de Clarendon.
15. Andrews 1976 , págs. 70, 97.
16. Nathanson 2000 , págs. 475-85.
17. Erdős, Pál (1942). "Sobre una prueba elemental de algunas fórmulas asintóticas en la teoría de particiones". Ana. Matemáticas . (2). 43 (3): 437–450. doi : 10.2307 / 1968802 . JSTOR 1968802 . Zbl 0061.07905 .  
18. Nathanson 2000 , p. 495.
19. Nathanson 2000 , págs. 458-64.
20. Andrews 1976 , págs. 33-34.
21. ver, por ejemplo, Stanley 1999 , p. 58

Referencias

• Abramowitz, Milton ; Stegun, Irene (1964). Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas . Departamento de Comercio de los Estados Unidos, Oficina Nacional de Normas. ISBN 0-486-61272-4.
• Andrews, George E. (1976). La teoría de las particiones . Prensa de la Universidad de Cambridge. ISBN 0-521-63766-X.
• Andrews, George E .; Eriksson, Kimmo (2004). Particiones enteras . Prensa de la Universidad de Cambridge. ISBN 0-521-60090-1.
• Apostol, Tom M. (1990) [1976]. Funciones modulares y series de Dirichlet en teoría de números . Textos de Posgrado en Matemáticas . 41 (2ª ed.). Nueva York, etc .: Springer-Verlag . ISBN 0-387-97127-0. Zbl  0697.10023 . (Véase el capítulo 5 para una introducción pedagógica moderna a la fórmula de Rademacher) .
• Bóna, Miklós (2002). Un recorrido por la combinatoria: una introducción a la enumeración y la teoría de grafos . Publicaciones científicas mundiales. ISBN 981-02-4900-4. (una introducción elemental al tema de las particiones enteras, incluida una discusión de los gráficos de Ferrers)
• Hardy, GH ; Wright, EM (2008) [1938]. Introducción a la teoría de los números . Revisado por DR Heath-Brown y JH Silverman . Prólogo de Andrew Wiles . (6ª ed.). Oxford: Prensa de la Universidad de Oxford . ISBN 978-0-19-921986-5. Señor  2445243 . Zbl  1159.11001 .
• Lehmer, DH (1939). "Sobre el resto y convergencia de la serie para la función de partición" . Trans. Amer. Matemáticas. Soc . 46 : 362–373. doi : 10.1090 / S0002-9947-1939-0000410-9 . Señor  0000410 . Zbl  0022.20401 .Proporciona la fórmula principal (sin derivados), el resto y la forma anterior para A _k ( n ).)
• Gupta, Hansraj; Gwyther, CE; Miller, JCP (1962). Real Sociedad de Matemáticas. Tablas . Volumen 4, Tablas de particiones. (Tiene texto, bibliografía casi completa, pero ellos (y Abramowitz) omitieron la fórmula de Selberg para A _k ( n ), que está en Whiteman).
• Macdonald, Ian G. (1979). Funciones simétricas y polinomios de Hall . Monografías matemáticas de Oxford. Prensa de la Universidad de Oxford . ISBN 0-19-853530-9. Zbl  0487.20007 . (Ver sección I.1)
• Nathanson, MB (2000). Métodos elementales en teoría de números . Textos de Posgrado en Matemáticas. 195 . Springer-Verlag . ISBN 0-387-98912-9. Zbl  0953.11002 .
• Rademacher, Hans (1974). Documentos recopilados de Hans Rademacher . v II . Prensa del MIT. págs. 100–07, 108–22, 460–75.
• Sautoy, Marcus Du. (2003). La música de los Primes . Nueva York: Perennial-HarperCollins.
• Stanley, Richard P. (1999). Combinatoria enumerativa . Volúmenes 1 y 2. Cambridge University Press. ISBN 0-521-56069-1.
• Whiteman, AL (1956). "Una suma relacionada con la serie para la función de partición" . Pacific Journal of Mathematics . 6 (1): 159-176. doi : 10.2140 / pjm.1956.6.159 . Zbl  0071.04004 . (Proporciona la fórmula de Selberg. La forma más antigua es la expansión finita de Fourier de Selberg).

Enlaces externos

• "Partición" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Calculadora de partición y composición
• Weisstein, Eric W. "Partición" . MathWorld .
• Wilf, Herbert S. Lectures on Integer Partitions (PDF) , archivado (PDF) del original el 24 de febrero de 2021 , consultado el 28 de febrero de 2021
• Contar con particiones con tablas de referencia a la Enciclopedia en línea de secuencias de enteros
• Entrada de particiones enteras en la base de datos FindStat
• Integer :: Partition Perl module de CPAN
• Algoritmos rápidos para generar particiones enteras
• Generación de todas las particiones: una comparación de dos codificaciones
• Grime, James (28 de abril de 2016). "Particiones - Numberphile" (video) . Brady Haran . Consultado el 5 de mayo de 2016 .